16.2: Movimiento bajo una Fuerza Central

No existe una solución analítica general en términos de funciones algebraicas simples para el problema de tres cuerpos gravitatorios de masas comparables. Excepto en algunos casos muy específicos el problema tiene que resolverse numéricamente. Sin embargo, en el problema restringido de los tres cuerpos, imaginamos que hay dos cuerpos de masas comparables que giran alrededor de su centro de masa común\(\text{C}\), y un tercer cuerpo de masa insignificante se mueve en el campo de los otros dos. Consideramos este problema parcialmente en la Sección 16.1, salvo que restringimos aún más nuestro interés en limitar nuestra atención a la línea que se une a dos masas principales. En esta sección ampliaremos nuestra atención. Una pregunta que hicimos en la sección 16.1 fue: ¿Hay algún punto donde un tercer cuerpo de masa insignificante pueda orbitar alrededor\(\text{C}\) con el mismo periodo que las otras dos masas? Encontramos tres de estos puntos, los colineales lagrangianos, en la línea que une las dos masas principales. En esta sección descubriremos dos puntos adicionales, el cuarto y quinto puntos lagrangianos. No son colineales con\(M_1\) y\(M_2\), sino que son tales que las tres masas están en las esquinas de un triángulo equilátero.

Trabajaremos en un marco de referencia co-rotativo en el que existen dos pozos de potencial hiperbólico profundo de la forma\(−GM_1 /r_1\) y\(−GM_2 /r_2\) del campo gravitacional de las dos masas principales hundidas en el potencial paraboloide nasal de la forma\(-\frac{1}{2} ρ^2 ω^2\), cuya derivada negativa es la centrífuga fuerza por unidad de masa. Aquí\(ρ\) está la coordenada cilíndrica habitual, y\(ω^2 = G(M_1 + M_2 ) / a^3 \).

\(\text{FIGURE XVI.7}\)

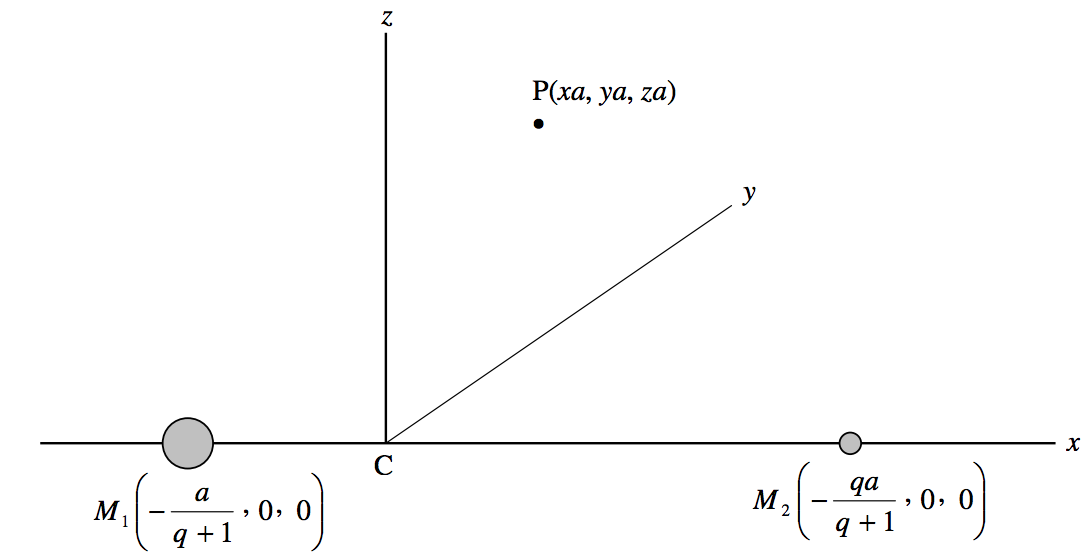
En la figura\(\text{XVI.7}\) vemos un sistema de coordenadas que gira alrededor del\(z\) eje, de tal manera que las dos masas principales permanecen en el eje x, y el origen de las coordenadas es el centro de masa\(\text{C}\). La relación de masa\(M_1/M_2 = q\), por lo que las coordenadas de las dos masas son como se muestra en la figura. La distancia constante entre las dos masas es\(a\). \(\text{P}\)es un punto cuyas coordenadas son\((xa, \ ya , \ za), \ x, \ y\) y\(z\) siendo adimensionales. El potencial efectivo gravitacional-más-centrífugo\(V\) en\(P\) es

\[V = - \frac{GM_1}{a \left[ \left( x + \frac{1}{q + 1} \right)^2 + y^2 + z^2 \right]^{1/2}} - \frac{GM_2}{a \left[ \left( x - \frac{q}{q + 1} \right)^2 + y^2 + z^2 \right]^{1/2}} - \frac{G(M_1 + M_2)(x^2 + y^2)}{2a}. \label{16.2.1} \tag{16.2.1}\]

Dejar\(W = \frac{Va}{G(M_1 + M_2)}\) (adimensional). Entonces

\[W = - \frac{q}{ \left[ \left( 1 + x (q+1) \right)^2 + (y^2 + z^2 ) (q+1)^2 \right]^{1/2}} - \frac{1}{\left[ \left( q - x(q+1) \right)^2 + (y^2 + z^2)(q+1)^2 \right]^{1/2}} - \frac{x^2 + y^2}{2} . \label{16.2.2} \tag{16.2.2}\]

Escribiré esto para abreviar:

\[W = -Aq - B - \frac{1}{2} ( x^2 + y^2 ) . \label{16.2.3} \tag{16.2.3}\]

Aquí\(A\) y\(B\) son funciones con significado obvio a partir de la comparación con la Ecuación\ ref {16.2.2}.

Vamos a necesitar la primera y la segunda derivada, así que las enumero aquí, en las que, por ejemplo,\(W_{xy}\) es la abreviatura de\(\partial^2 W / \partial x \partial y\).

\[W_x = -(q + 1) [-q \left(1 + x) ( q+1) \right) A^3 + \left( q - x) (q + 1) \right) B^3 ] - x , \label{16.2.4} \tag{16.2.4}\]

\[W_y = (q + 1)^2 y [q A^3 + B^3 ] - y , \label{16.2.5} \tag{16.2.5}\]

\[W_z = (q + 1 )^2 z [q A^3 + B^3], \label{16.2.6} \tag{16.2.6}\]

\[W_{xx} = -(q + 1)^2 [3q \left( 1 + x(q+1) \right)^2 A^5 - qA^3 + 3 \left( q -x (q+1) \right)^2 B^5 - B^3 ] - 1 , \label{16.2.7} \tag{16.2.7}\]

\[W_{yy} = - (q + 1)^2 [3q (q+1)^2 y^2 A^5 - q A^3 + 3 (q+1)^2 y^2 B^5 - B^3] - 1, \label{16.2.8} \tag{16.2.8}\]

\[W_{zz} = -(q + 1)^2 [3q ( q + 1)^2 z^2 A^5 - q A^3 + 3 (q + 1)^2 z^2 B^5 - B^3], \label{16.2.9} \tag{16.2.9}\]

\[W_{yz} = W_{zy} = -3 (q + 1)^4 yz (qA^5 + B^5) , \label{16.2.10} \tag{16.2.10}\]

\[W_{zx} = W_{xz} = -3 ( q+ 1)^3 z [q \left( 1 + x (q + 1) \right) A^5 - \left( q - x(q + 1) \right) B^5 ] , \label{16.2.11} \tag{16.12.11}\]

\[W_{xy} = W_{yz} = -3(q+1)^3 y [q \left( 1 + x(q + 1) \right) A^5 - \left( q - x (q+1) \right) B^5 ] . \label{16.2.12} \tag{16.2.12}\]

Es un poco difícil de dibujar\(W(x, y, z)\), pero podemos mirar el avión\(z = 0\) y ahí mirar\(W(x, y)\). La figura\(\text{XVI.8}\) es una gráfica de contorno de la superficie, para\(q = 5\), trazada por Mathematica por Mr Max Fairbairn de Sydney, Australia. Ya hemos visto, en figura\(\text{XVI.5}\), una sección a lo largo del\(x\) eje -eje.

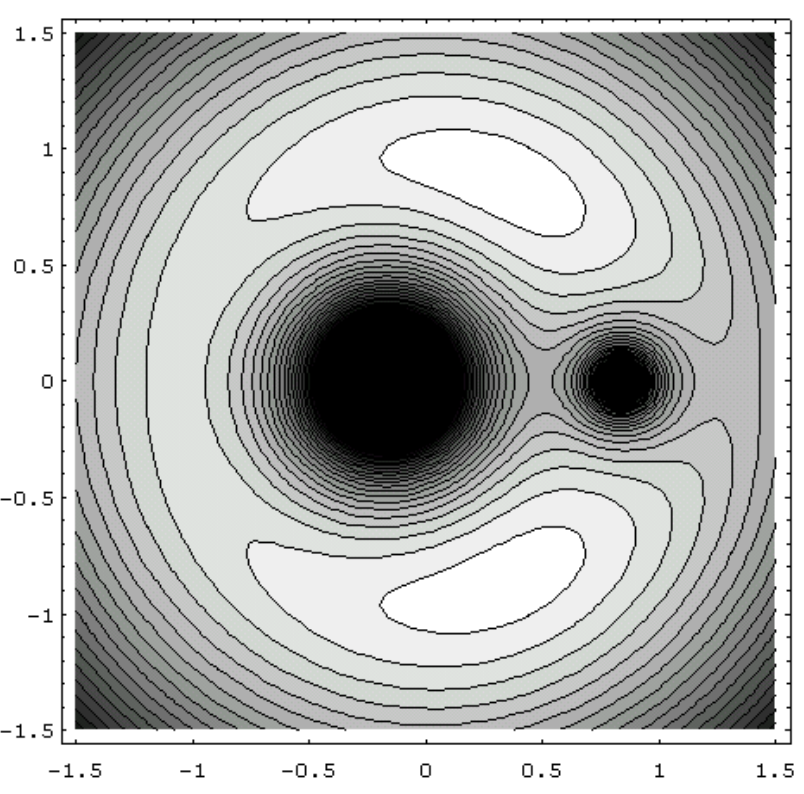
\(\text{FIGURE XVI.8}\)

La figura\(\text{XVI.9a}\) muestra un dibujo tridimensional de la superficie potencial equivalente en el plano, también trazada por Mathematica por Mr Fairbairn. La figura\(\text{XVI.9b}\) es un modelo de la superficie, visto desde más o menos arriba. Este fue construido en madera por el señor David Smith de la Universidad de Victoria, Canadá, y fotografiado por el señor David Balam, también de la Universidad de Victoria. La relación de masa es\(q = 5\).

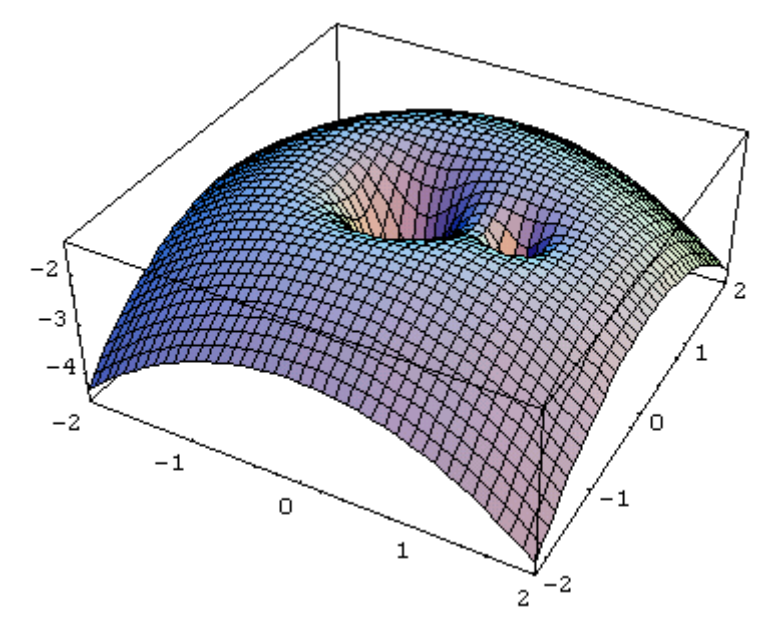
\(\text{FIGURE XVI.9A}\)

\(\text{FIGURE XVI.9B}\)

Podemos imaginar el camino tomado por una pequeña partícula en el campo de las dos masas principales imaginando una pequeña bola rodando o deslizándose sobre la superficie potencial equivalente. Podría rodar en uno de los dos pozos de potencial hiperbólico profundo que representan la atracción gravitacional de las dos masas. O podría rodar por los lados del gran paraboloide, es decir, podría ser arrojado hacia afuera por el efecto de la fuerza centrífuga. Debemos recordar, sin embargo, que la superficie representa el potencial equivalente referido a un marco co-rotatorio, y que, cada vez que la partícula se mueve con relación a este marco, experimenta una fuerza de Coriolis en ángulo recto con su velocidad.

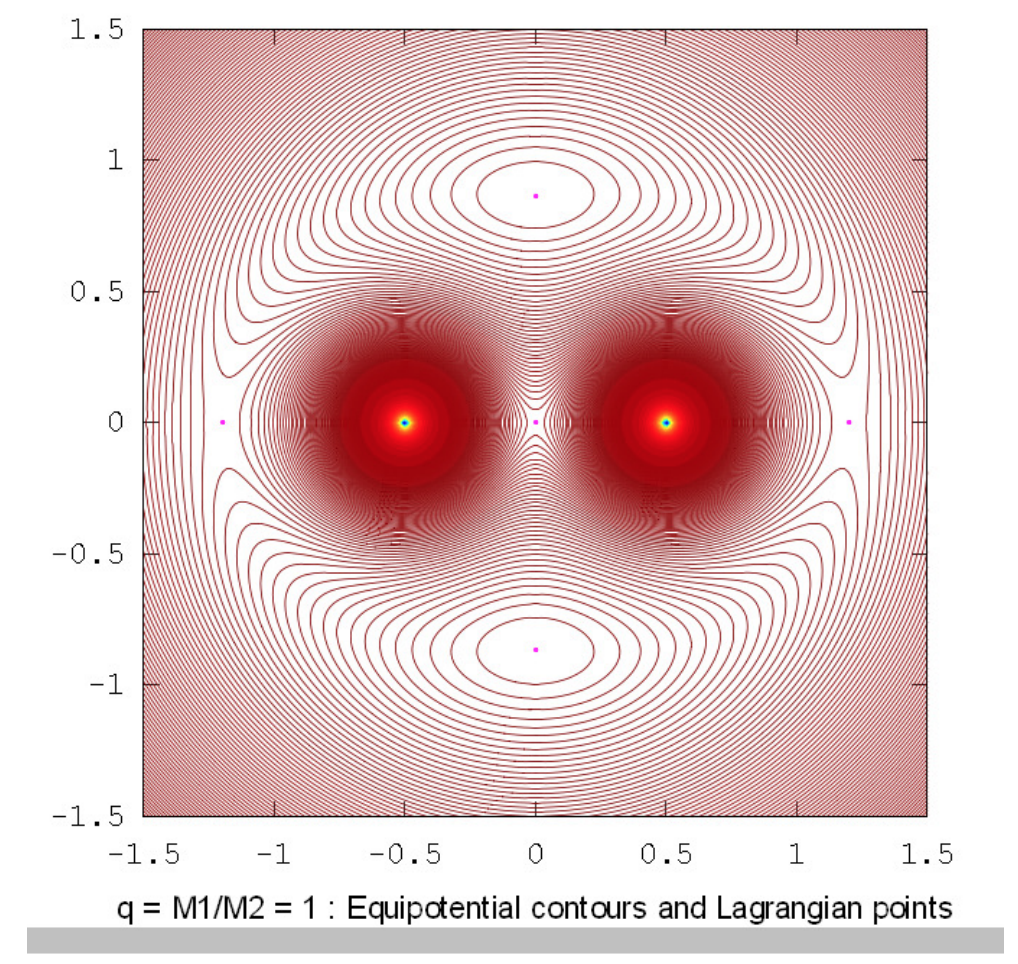
Los tres puntos lagrangianos colineales son en realidad puntos de silla de montar. A lo largo del eje x (figura XVI.5, son máximos, pero cuando el potencial se traza paralelo al eje y, son mínimos. No obstante, en esta sección, nos interesarán particularmente los puntos equiláteros, cuyas coordenadas (verificar esto) son. \(x_{\text{L}} = \frac{1}{2} \left( \frac{q-1}{q+1} \right) , \ y_{\text{L}} = \pm \frac{\sqrt{3}}{2}\). Puedes verificar a partir de las Ecuaciones 16.2.4 y 5, (aunque es posible que necesites algo de paciencia para hacerlo) que las primeras derivadas son cero ahí. Se necesitaría aún más paciencia y determinación para determinar a partir de las segundas derivadas que el potencial equivalente es un máximo allí, aunque quizás prefieras mirar figuras\(\text{XVI.8}\) y en\(\text{9}\) lugar de atravesar ese álgebra. Yo he hecho el álgebra y puedo decirles que las primeras derivadas en los puntos equiláteros son efectivamente cero y las segundas derivadas son las siguientes.

\[W_{xx} = - \frac{3}{4}, \quad W_{yy} = -\frac{9}{4}, \quad W_{zz} = +1, \quad W_{yz} = W_{zx} = 0, \quad W_{xy} = -\frac{3\sqrt{3}}{4} \left( \frac{q-1}{q+1} \right) . \]

Porque\(W_{zz} = +1\), el potencial en los puntos equiláteros pasa por un mínimo a medida que cruzamos el plano; en el plano, sin embargo,\(W\) es un máximo, y tiene el valor ahí de

\[-\frac{3q^2 + 5q + 3}{2(q + 1)^2} . \]

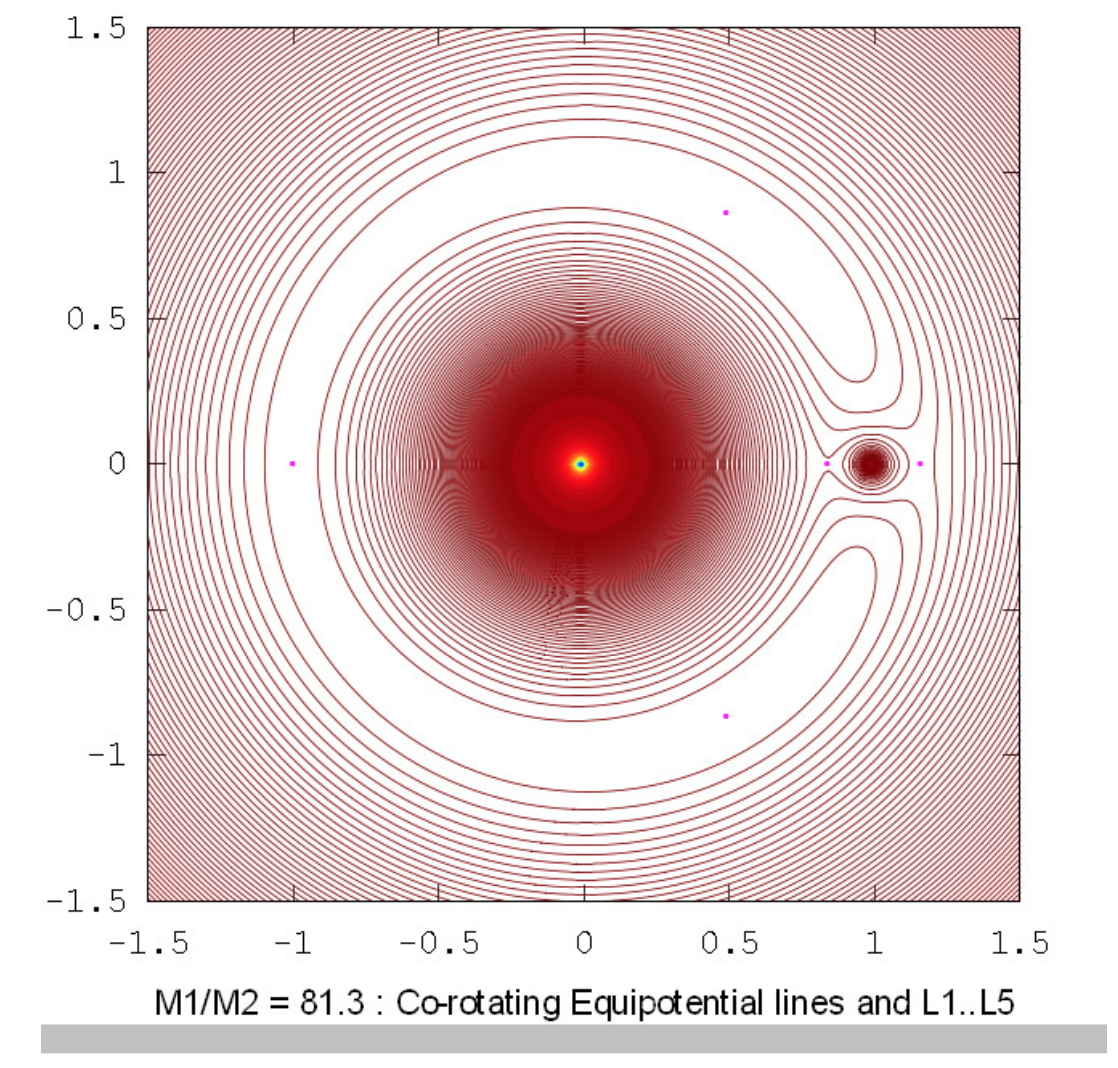
En materia de notación, los puntos equiláteros a menudo se denominan los puntos lagrangianos cuarto y quinto, denotados por\(\text{L}_4\) y\(\text{L}_5\). Surge entonces la pregunta, ¿cuál es\(\text{L}_4\) y cuál es\(\text{L}_5\)? La mayoría de los autores etiquetan el punto equilátero que conduce a la menos masiva de las dos masas principales por\(60^\circ\)\(\text{L}_4\) y la que recorre\(60^\circ \ \text{L}_5\). Esto sería inequívoco si limitáramos nuestro interés, por ejemplo, a asteroides troyanos de planetas en órbita alrededor del Sol, o Calypso que lleva a Tetis en órbita alrededor de Saturno y Telesto que sigue a Tetis. Habría ambigüedad, sin embargo, si los dos cuerpos principales tuvieran masas iguales, o si los dos cuerpos principales fueran miembros de un par binario cercano de estrellas en el que la transferencia masiva llevó a que la estrella más masiva se convirtiera en la menos masiva. En casos tan especiales, tendríamos que tener cuidado para dejar claro nuestro significado. Por el momento, sin embargo, asumiré que los dos cuerpos principales tienen masas desiguales, y el punto equilátero que precede al cuerpo menos masivo es\(\text{L}_4\).

En figura\(\text{XVI.10}\) estamos mirando en el\(xy\) -plano. He marcado un punto\(\text{P}\), con coordenadas\((x, y, z)\); éstas se expresan en unidades de\(a\), la separación constante de las dos masas principales. El origen de las coordenadas es el centro de masa\(\text{C}\) y se muestran las coordenadas (en unidades de\(a\)) de las dos masas. El vector de momento angular ω se dirige a lo largo de la dirección de aumento\(z\).

Ahora imagina una partícula de masa\(m\) en\(\text{P}\). Estará sujeto a una fuerza dada por lo negativo del gradiente de la energía potencial, que es\(m\) veces el potencial. Así en la\(x\) -dirección,\(ma \ddot{x} = - m \frac{\partial V}{a \partial x}\). Además de esta fuerza, sin embargo, siempre que está en movimiento con relación al marco co-giratorio está sujeto a una fuerza Coriolis\(2m \textbf{v}×\textbf{ω}\). Así es el\(x\) -componente de la Ecuación del movimiento\(ma \ddot{x} = -m \frac{\partial V}{a \partial x} + 2mω a \dot{y}\). Dividiendo por\(ma\) encontramos para la Ecuación de movimiento en la\(x\) dirección -dirección

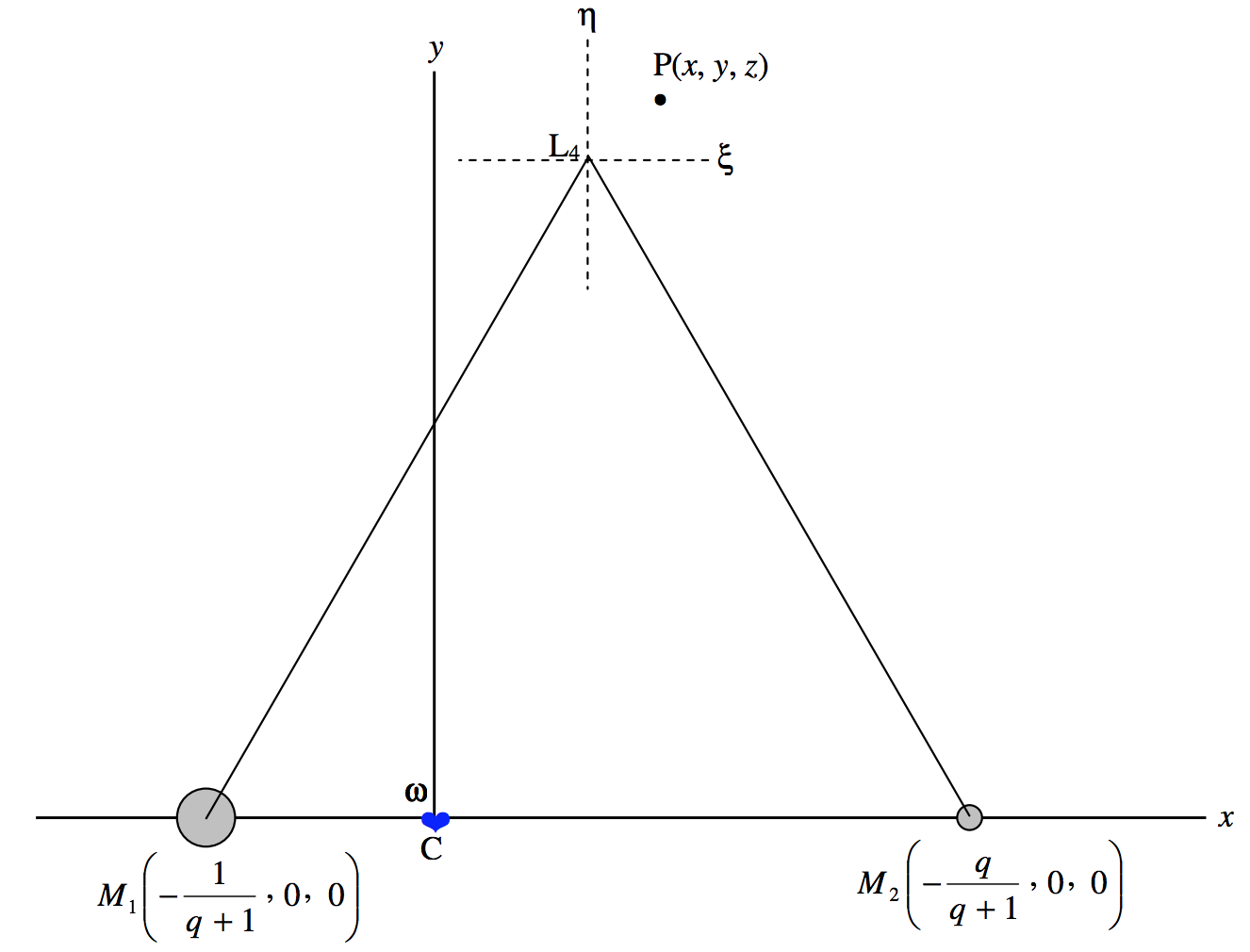
\(\text{FIGURE XVI.10}\)

\[\ddot{x} = -\frac{1}{a^2} \frac{\partial V}{\partial x} + 2ω \dot{y} . \label{16.2.13} \tag{16.2.13}\]

De igual manera en las otras dos direcciones, tenemos

\[\ddot{y} = -\frac{1}{a^2} \frac{\partial V}{\partial y} - 2ω \dot{x} \label{16.2.14} \tag{16.2.14}\]

y\[\ddot{z} = -\frac{1}{a^2} \frac{\partial V}{\partial z}. \label{16.2.15} \tag{16.2.15}\]

Estas, entonces, son las Ecuaciones diferenciales que rastrearán el movimiento de una partícula que se mueve en las proximidades de las dos masas orbitantes principales. Para grandes excursiones, mejor se resuelven numéricamente. Sin embargo, las soluciones cercanas a los puntos equiláteros se prestan a una solución analítica simple, la cual intentaremos aquí. Empecemos, entonces, por referir posiciones a coordenadas con origen en un punto lagrangiano ecuatorial. Las coordenadas del punto\(\text{P}\) con respecto al punto lagrangiano son\((ξ, η, ζ )\), donde\(ξ = x - x_L , \ η = y - y_L, ζ = z\). Tenga en cuenta también que\(\dot{ξ} = \dot{x} \ \ddot{ξ} =\ddot{x}\), etc. vamos a necesitar las derivadas del potencial cerca de los puntos lagrangianos, y, por el teorema de Taylor (¡o simplemente sentido común!) estos son dados por

\[V_x = (V_x )_\text{L} + ξ (V_{xx} )_\text{L} + η (V_{yx})_\text{L} + ζ (V_{zx} )_\text{L} , \label{16.2.16} \tag{16.2.16}\]

\[V_y = (V_y )_\text{L} + ξ (V_{xy} )_\text{L} + η (V_{yy})_\text{L} + ζ (V_{zy} )_\text{L} , \label{16.2.17} \tag{16.2.17}\]

\[V_z = (V_z )_\text{L} + ξ (V_{xz} )_\text{L} + η (V_{yz})_\text{L} + ζ (V_{zz} )_\text{L} , \label{16.2.18} \tag{16.2.18}\]

Ya hemos trabajado las derivadas en los puntos lagrangianos (las primeras derivadas son cero), así que ahora podemos poner estas expresiones en las Ecuaciones 16.2.13,14 y 15, para obtener

\[\ddot{ξ} - 2ω \dot{η} = ω^2 \left( \frac{3}{4} ξ + \frac{3 \sqrt{3} (q-1)}{4(q+1)} η \right) , \label{16.2.19} \tag{16.2.19}\]

\[\ddot{η} + 2ω\dot{ξ} = ω^2 \left( \frac{3\sqrt{3}(q-1)}{4(q+1)}ξ + \frac{9}{4} η \right) \label{16.2.20} \tag{16.2.20}\]

y\[\ddot{ζ} = - ω^2 ζ . \label{16.2.21} \tag{16.2.21}\]

La última de estas Ecuaciones nos dice que los desplazamientos en la\(z\) dirección -son periódicos con periodo igual al periodo de los dos cuerpos orbitantes principales. El movimiento es acotado y estable perpendicular al plano. Una órbita inclinada al plano de las órbitas que contiene\(M_1\) y\(M_2\) es estable.

Para y η, busquemos soluciones periódicas de la forma

\[\ddot{ξ} = n^2 ξ \text{ and } \ddot{η} = n^2 η \label{16.2.22a,b} \tag{16.2.22a,b}\]

para que

\[\dot{ξ} = in ξ \text{ and } \dot{η} = in η \label{16.2.23a,b} \tag{16.2.23a,b}\]

donde\(n\) es real y por lo tanto\(n^2\) es positivo.

La sustitución de estos en las Ecuaciones 16.2.19-21 da

\[(n^2 + \frac{3}{4} ω^2) ξ + \left( wωni + \frac{3\sqrt{3}}{4} \left( \frac{q-1}{q+1} \right) ω^2 \right) η = 0 \label{16.2.24} \tag{16.2.24}\]

y\[\left( 2ω ni - \frac{3\sqrt{3}}{4} \left( \frac{q-1}{q+1} \right) ω^2 \right)ξ - (n^2 + \frac{9}{4} ω^2 ) η = 0. \label{16.2.25} \tag{16.2.25}\]

Una solución trivial es\(ξ = η = 0\); es decir, la partícula es estacionaria en el punto lagrangiano. Si bien esta es efectivamente una solución posible, es inestable, ya que el potencial es un máximo ahí. Las soluciones no triviales se encuentran estableciendo el determinante de los coeficientes igual a cero. Así

\[n^4 - ω^2 n^2 + \frac{27qω^4}{4(q+1)^2} = 0 . \label{16.2.26} \tag{16.2.26}\]

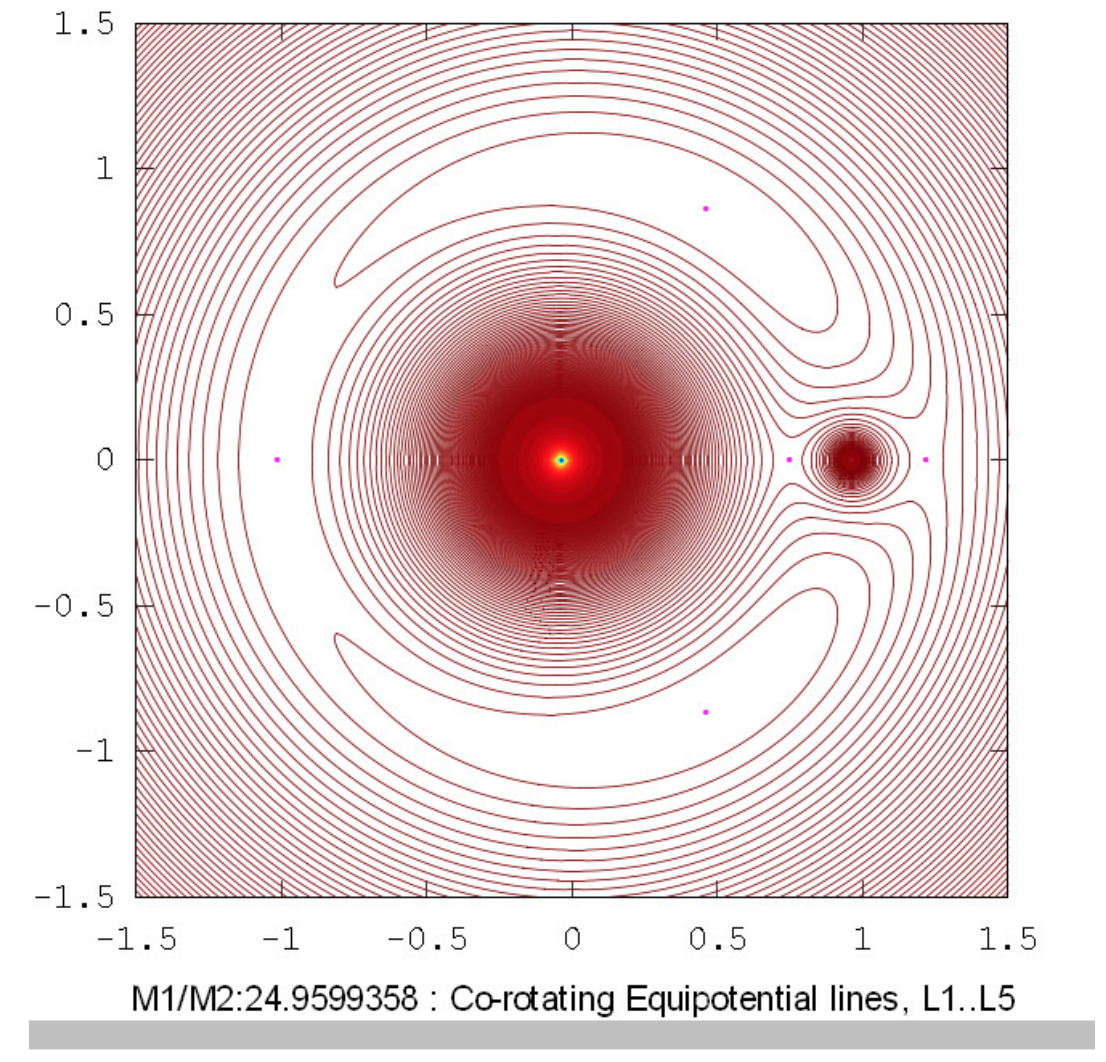
Esta es una Ecuación cuadrática en\(n^2\), y de verdad\(n^2\) debemos tener\(b^2 > 4ac\), o\(1 > \frac{27q}{(q+1)^2}\), o\(q^2 - 25q + 1 >0\). Es decir,\(q > 24.959 \ 935 \ 8\) o\(q < 1/24.959 \ 935 \ 8 = 0.040 \ 064 \ 206\). También requerimos\(n^2\) ser no sólo reales sino positivos. Las soluciones de Ecuación\(16.2.26\) son

\[2n^2 = ω^2 \left( 1 \pm \sqrt{1 - 27q/(1+q)^2} \right) . \label{16.2.27} \tag{16.2.27}\]

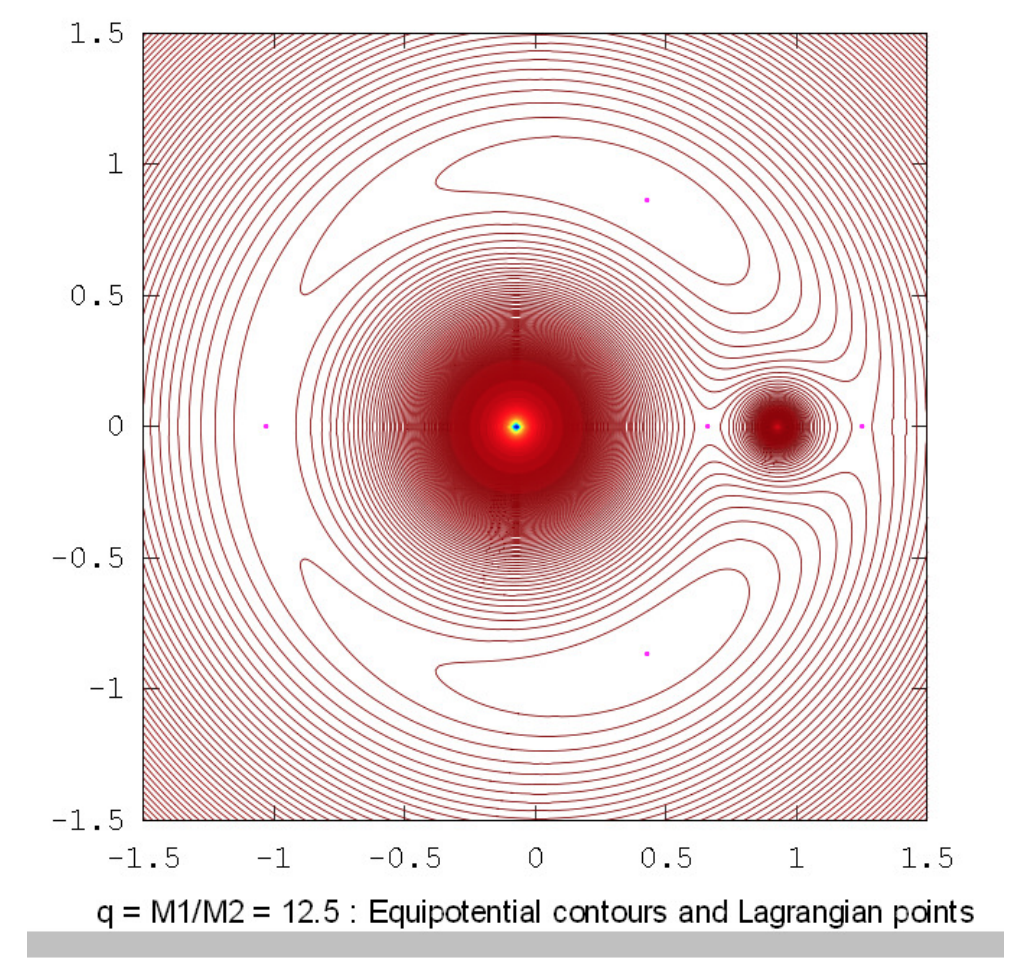
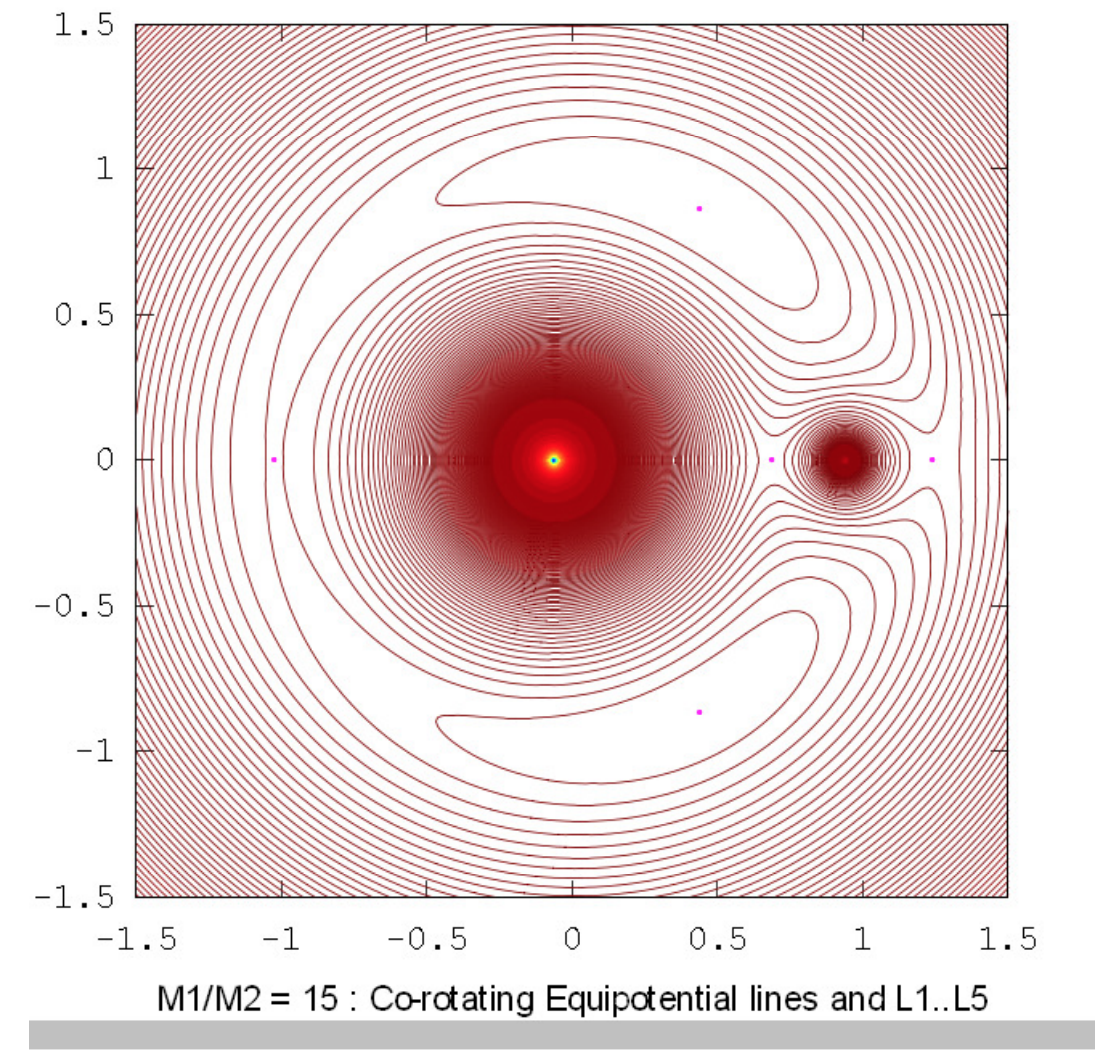
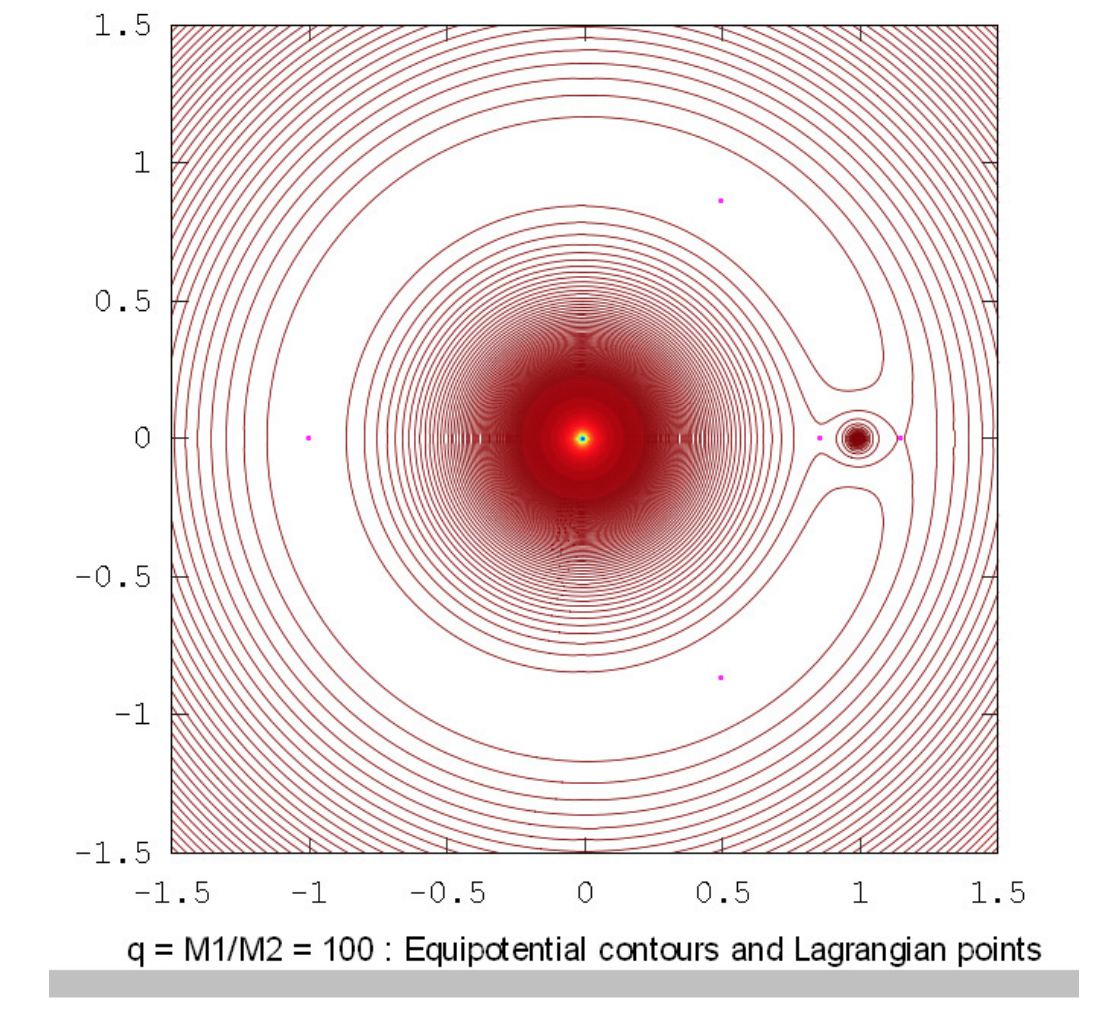
Para cualquier relación de masa\(q\) que sea menor\(0.040 \ 064 \ 206\) o mayor que\(24.959 \ 935 \ 8\) ambas soluciones son positivas. Así, son posibles órbitas elípticas estables (en el marco co-rotativo) alrededor de los puntos lagrangianos equiláteros si la relación de masa de las dos masas principales es mayor que aproximadamente 25, pero no de otra manera.

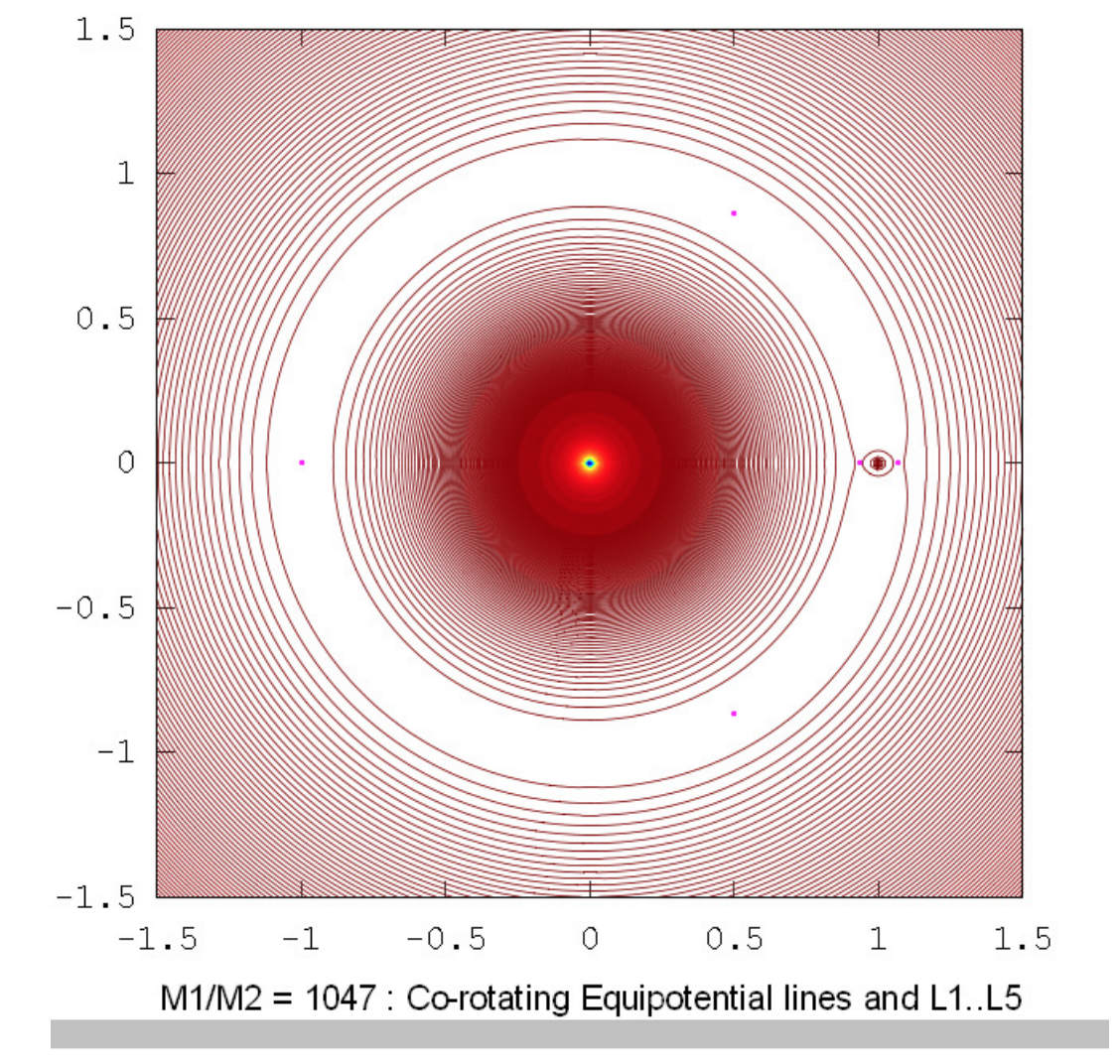
Si consideramos el sistema Sol-Júpiter, para lo cual\(q = 1047.35\), tenemos que

\(n = 0.996 757ω \text{ or } n = 0.080 464 5ω.\)

El período del movimiento alrededor del punto lagrangiano es entonces

\(P = 1.0033P_{\text{J}} \text{ or } P = 12.428P_\text{J}\)

Esta descripción del movimiento se aplica a asteroides que se mueven de cerca alrededor de los puntos lagrangianos equiláteros, y la aproximación realizada en el análisis apareció en la expansión Taylor para el potencial dado por las Ecuaciones 16.2.16-18. Para excursiones más distantes, uno podría probar soluciones analíticas al expandir la serie Taylor a términos de orden superior (y por supuesto elaborar las derivadas de orden superior) o podría ser más fácil integrar numéricamente las Ecuaciones 16.2.19 y 20. Mucha gente ha tenido una enorme cantidad de diversión con esto. Las órbitas no siguen exactamente los contornos equipotenciales, claro, pero en general la forma no son muy diferentes en apariencia de los contornos. Así, para excursiones más grandes desde los puntos lagrangianos las órbitas se estiran con una cola estrecha que se curva hacia\(\text{L}_1\); tales órbitas tienen un parecido fantasioso con la forma de un renacuajo y a menudo se las conoce como órbitas de renacuajo. Para más excursiones, un asteroide puede comenzar cerca\(\text{L}_4\) y rodar cuesta abajo, virándose alrededor de la parte posterior del cuerpo más masivo, a través del\(\text{L}_1\) punto y luego hacia arriba hacia\(\text{L}_5\); luego se desliza de nuevo, vuelve a atravesar\(\text{L}_1\) y luego hacia arriba de\(\text{L}_4\) nuevo, y así sucesivamente. Se trata de una llamada órbita de herradura.

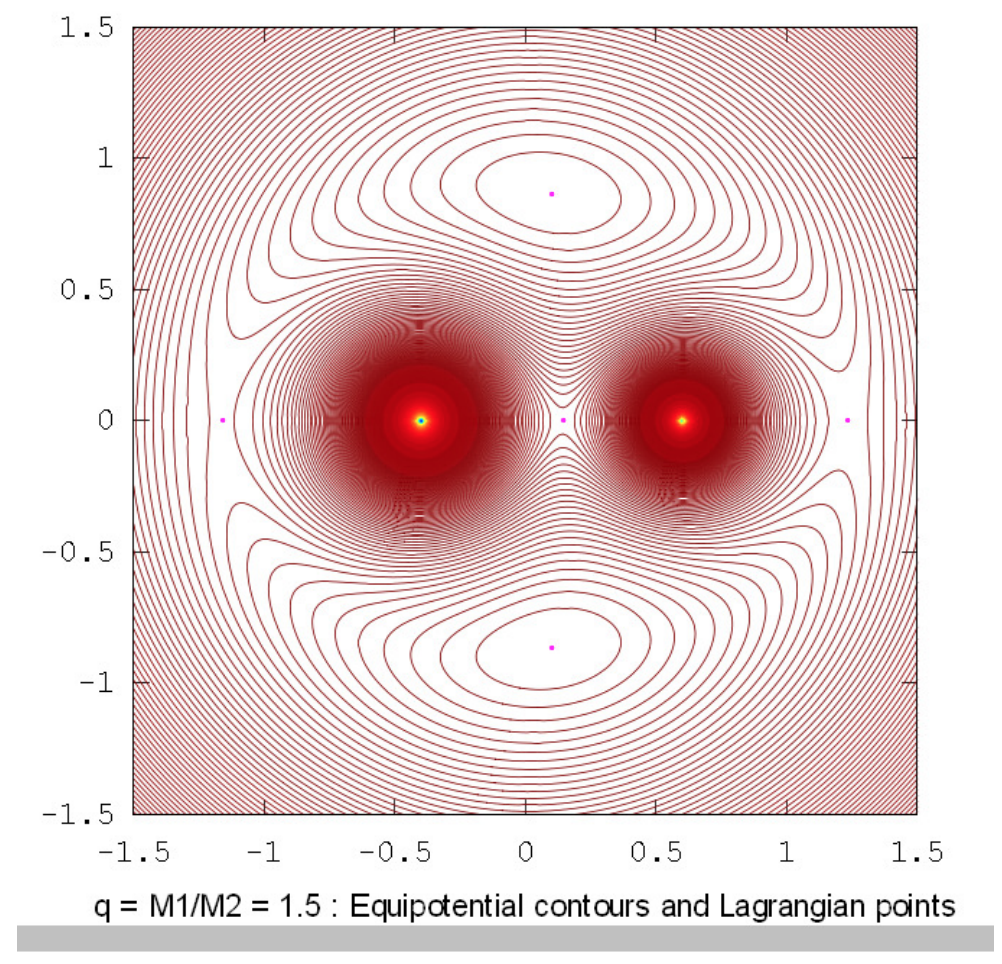
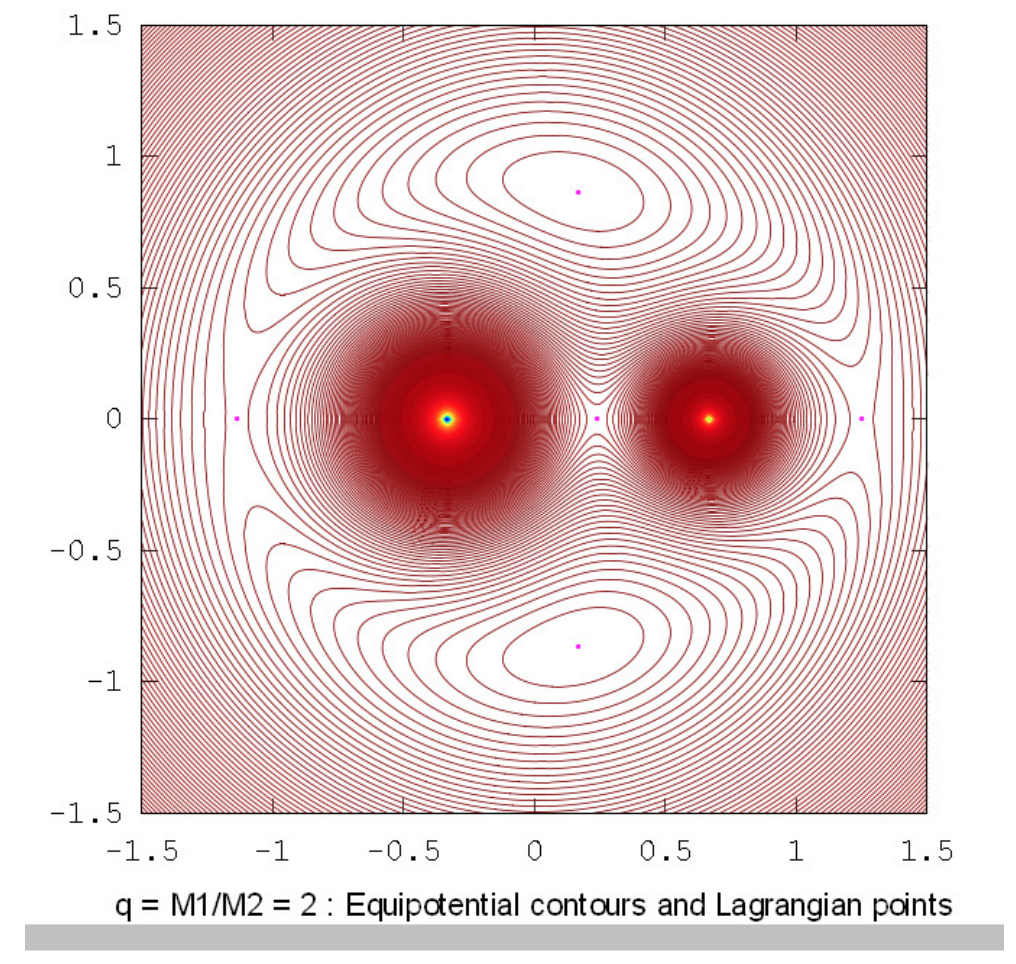
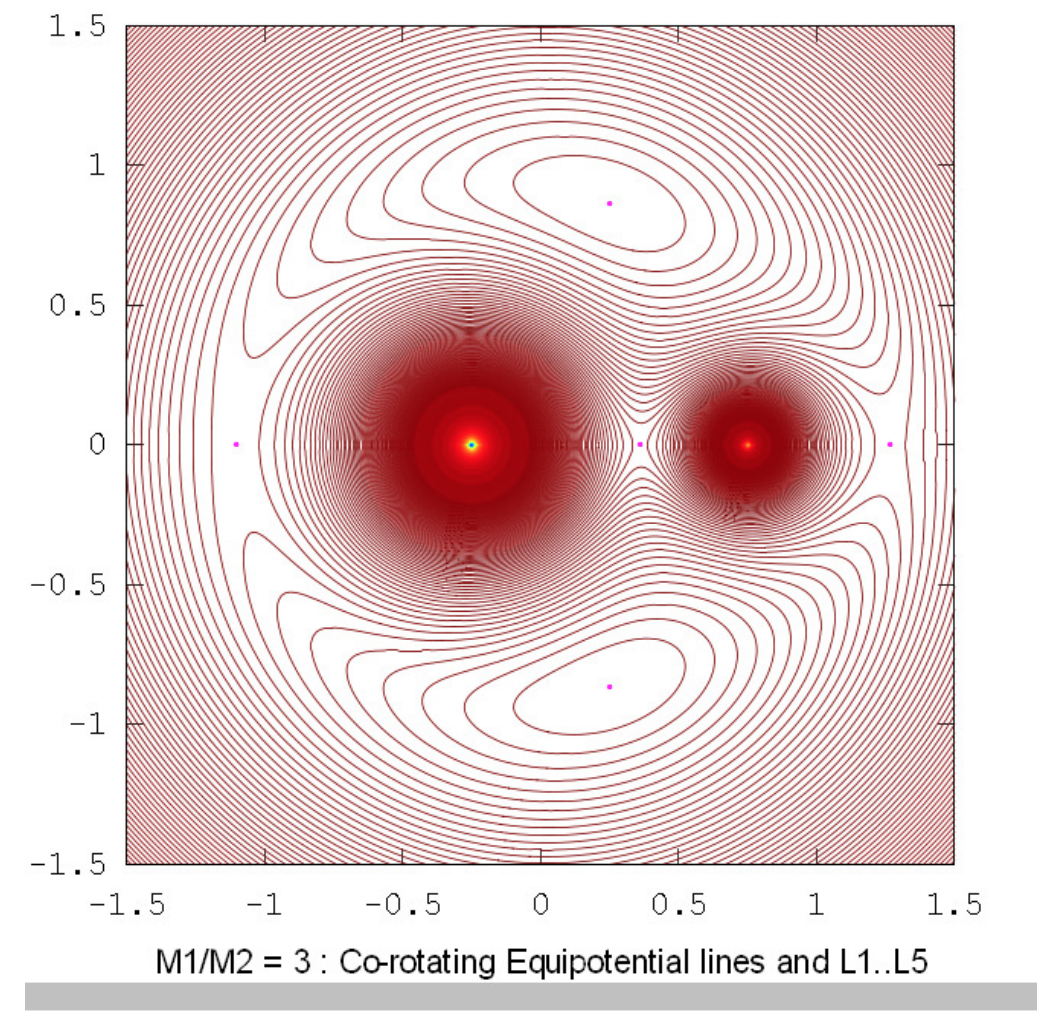
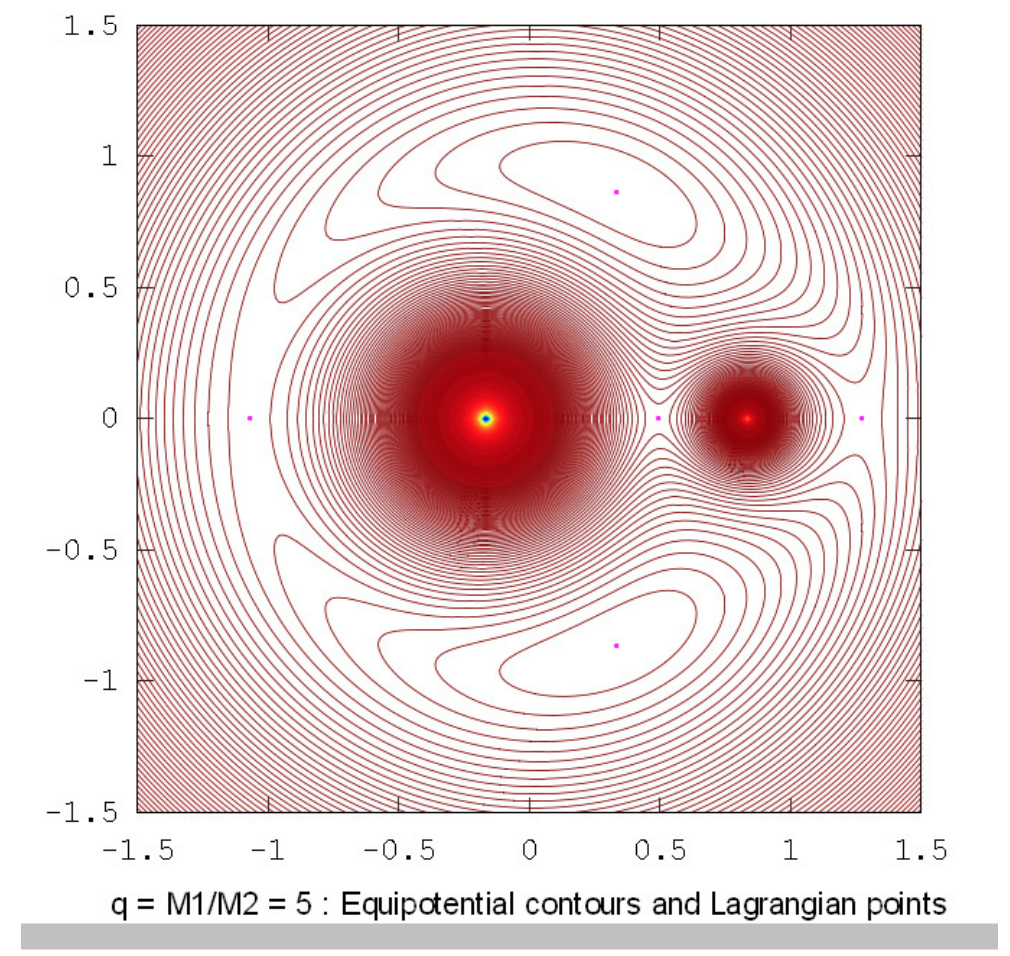
Los dibujos a continuación muestran los contornos equipotenciales para una serie de relaciones de masa. Estos dibujos fueron elaborados utilizando Octave por el Dr. Mandayam Anandaram de la Universidad de Bangalore, y son dedicados por él al fallecido Max Fairbairn de Sydney, Australia, quien preparó figuras\(\text{XVI.8}\) y\(\text{XVI.9a}\) para mí poco antes de su prematura muerte. Anand y Max fueron mis primeros estudiantes de posgrado en la Universidad de Victoria, Canadá, hace muchos años. Estos dibujos muestran la evolución gradual de contornos en forma de renacuajo a contornos en forma de herradura. La relación masa-masa\(q = 24.959 \ 935 \ 8\) es la relación crítica por debajo de la cual orbita estable alrededor de los puntos equiláteros\(\text{L}_4\) y no\(\text{L}_5\) son posibles. Las relaciones de masa\(q = 81.3\) y\(1047\) son las proporciones para los sistemas Tierra-Luna y Sol-Júpiter respectivamente. El lector notará que, en lugares donde los contornos están muy espaciados, en particular cerca del pozo potencial profundo de la masa más grande, aparecen franjas de Moiré. Estas franjas aparecen donde la separación del contorno es comparable al tamaño de píxel, y el lector las reconocerá como franjas de Moiré y, pensamos, no serán engañadas por ellas.

El Dr. Anandaram también ha preparado una serie de dibujos fascinantes en los que se superponen órbitas de muestra, en un segundo color, sobre los contornos equipotenciales. Estas incluyen órbitas de renacuajo en las inmediaciones de los puntos equiláteros; órbitas “triangulares” de los asteroides Hilda, que se encuentran en resonancia 2:3 con Júpiter; la órbita casi “cuadrada” de Thule, que está en resonancia 3:4 con Júpiter; y la mitad de un período completo de libración de 9940 años de Plutón, que está en 3:2 resonancia con Neptuno. Se propone publicarlos en un artículo separado dedicado a Max, cuya referencia en su momento se dará en estas notas.