2.6: Dos electrodos semicíclicos

Esta sección requiere que el lector esté familiarizado con funciones de una variable compleja y transformaciones conformes. Para lectores que no estén familiarizados con estos, esta sección puede omitirse sin perjuicio de entender los siguientes capítulos. Para los lectores que están familiarizados, este es un buen ejemplo de transformaciones conformes para resolver un problema físico.

\(\text{FIGURE II.5}\)

Tenemos dos electrodos semicíclicos como se muestra en la Figura\(II\) .5. El potencial del superior es 0 y el potencial del inferior es\(V_0\). Supondremos que el radio del círculo es 1; o, lo que equivale a lo mismo, expresaremos coordenadas\(x\) y\(y\) en unidades del radio. Representemos la posición de cualquier punto cuyas coordenadas sean (x, y) por un número complejo\(z = x + iy\).

Ahora dejemos\(w = u + iv\) ser un número complejo relacionado con\(z\) por\(w=i\left (\frac{1-z}{1+z}\right )\); es decir,\(z=\frac{1+ iw}{1- iw}\). Sustituir\(w = u + iv \text{ and }z = x + iy\) en cada una de estas ecuaciones, e igualar partes reales e imaginarias, para obtener

\[\begin{align}\label{2.6.1}u&=\frac{2y}{(1+x)^2+y^2};\quad\quad &&v=\frac{1-x^2+y^2}{(1+x)^2+y^2};\\ x&=\frac{1-u^2-v^2}{u^2+(1+v)^2}; &&y=\frac{2u}{u^2+(1+v)^2}.\label{2.6.2}\end{align}\]

En ese caso, el semicírculo superior\((V = 0)\) en el\(xy\) plano -plano se mapea sobre el\(u\) eje positivo en el\(uv\) plano, y el semicírculo inferior\((V = V_0)\) en el\(xy\) plano -plano se mapea al\(u\) eje negativo en el\(uv\) plano. (Figura\(II\) .6.) Los puntos dentro del círculo delimitado por los electrodos en el\(xy\) plano -plano se mapean a puntos por encima del\(u\) eje\(uv\) -en el plano.

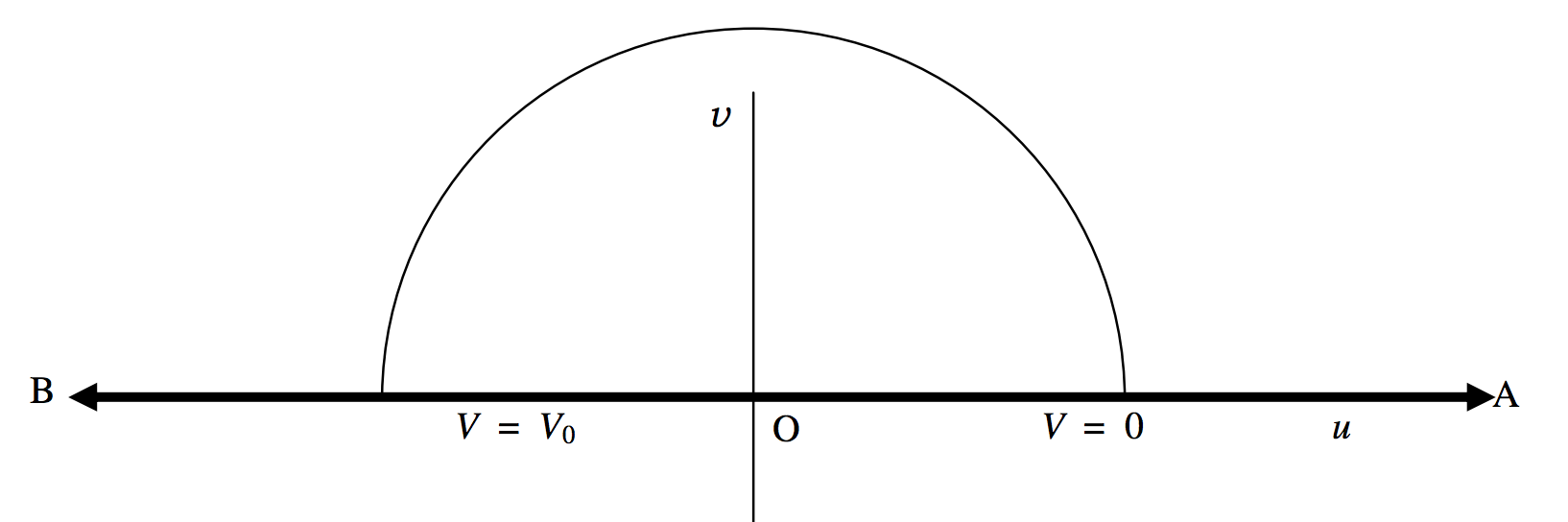
\(\text{FIGURE II.6}\)

En el\(uv\) plano -las líneas de fuerza son semicírculos, como la mostrada. El potencial va de 0 en un extremo del semicírculo a\(V_0\) en el otro, y así la ecuación a la línea semicircular de fuerza es

\[\label{2.6.3}\frac{V}{V_0}=\frac{\text{arg}\,w}{\pi}\]

o

\[\label{2.6.4}V=\frac{V_0}{\pi}\tan^{-1}(v/u).\]

Los equipotenciales (\(V\)= constante) son líneas rectas en el\(uv\) plano de la forma

\[\label{2.6.5}v=fu.\]

(Usted preferiría que usara el símbolo\(m\) para la pendiente de los equipotenciales, pero en un momento se alegrará de haber elegido el símbolo\(f\).)

Si ahora nos transformamos\(xy\) de nuevo al plano, vemos que la ecuación a las líneas de fuerza es

\[\label{2.6.6}V=\frac{V_0}{\pi}\tan^{-1} \left (\frac{1-x^2-y^2}{2y}\right ).\]

y la ecuación a los equipotenciales es

\[\label{2.6.7}1-x^2-y^2=2fy,\]

o

\[\label{2.6.8}x^2+y^2+2fy-1=0\]

Ahora bien, ¿no te alegra que haya elegido\(f\)? Aquellos que son útiles con secciones cónicas (ver Capítulo 2 de la Mecánica Celestial) entenderán que los equipotenciales en el\(xy\) plano son círculos de radios\(\sqrt{f^2 + 1}\), cuyos centros están en\((0 , \pm f )\), y que todos pasan por los puntos\((\pm 1 , 0)\). Se dibujan como líneas azules en la Figura\(II\) .7. Las líneas de fuerza son las trayectorias ortogonales a éstas, y son de la forma

\[\label{2.6.9}x^2+y^2+2gy+1=0\]

Estos son círculos de radios\(\sqrt{g^2 −1}\) y tienen sus centros en\((0 , \pm g)\). Se muestran como líneas rojas discontinuas en la Figura\(II\) .7.

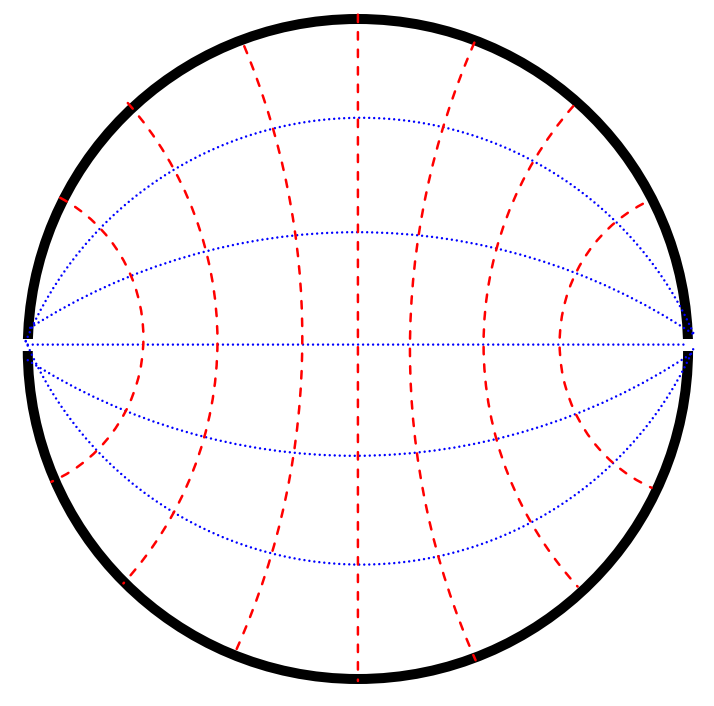
\(\text{FIGURE II.7}\)