2.3: Problemas de ejercicio

Ejercicio 2.1

Calcular la fuerza (por unidad de área) ejercida sobre una superficie conductora por un campo eléctrico externo, normal a ésta. Comparar el resultado con la definición del campo eléctrico dada por la Ec. (1.6), y comentar.

Ejercicio 2.2

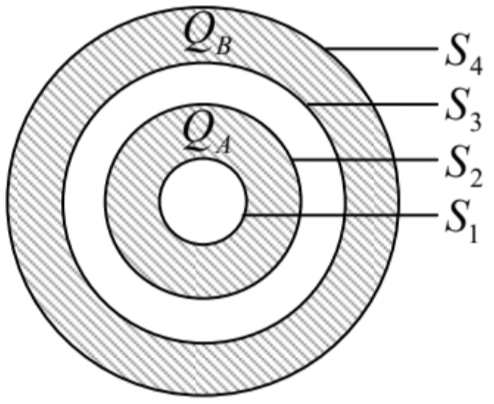
Carga eléctrica\(\ Q_{A}\) y se\(\ Q_{B}\) han colocado sobre dos conchas esféricas metálicas concéntricas — ver la figura a la derecha. ¿Cuál es la carga completa de cada una de las superficies\(\ S_{1}-S_{4}\)?

Ejercicio 2.3

Calcular la capacitancia mutua entre los terminales del circuito de condensador agrupado que se muestra en la figura de la derecha. Analizar e interpretar el resultado para casos particulares mayores.

Ejercicio 2.4

Calcular la capacitancia mutua entre los terminales del circuito semiinfinito de condensadores agrupados que se muestra en la figura de la derecha, y la ley de decaimiento de la tensión aplicada a lo largo del sistema.

Ejercicio 2.5

Un sistema de dos placas conductoras delgadas se ubica sobre un plano de tierra como se muestra en la figura de la derecha, donde\(\ A_{1}\) y\(\ A_{2}\) son las áreas de las partes de placa indicadas, mientras que\(\ d^{\prime}\) y\(\ d^{\prime \prime}\) son las distancias entre ellas. Descuidando los efectos marginales, calcule:

(i) la capacitancia efectiva de cada placa, y

ii) su capacitancia mutua.

Ejercicio 2.6

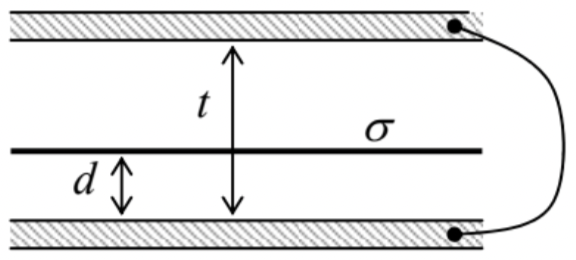
Una película plana ancha y delgada, que lleva una densidad de carga eléctrica uniforme\(\ \sigma\), se coloca dentro de un condensador plano cuyas placas están conectadas con un cable (ver la figura de la derecha), e inicialmente eran electroneutrales. Despreciando los efectos de borde, calcule las cargas superficiales de las placas y la fuerza neta que actúa sobre la película (por unidad de área).

Ejercicio 2.7

Siguiendo la discusión de dos esferas débilmente acopladas en la Sec. 2, encontramos una expresión aproximada de la capacitancia mutua (por unidad de longitud) entre dos alambres paralelos muy delgados, ambos con secciones transversales redondas, pero cada uno con su propio radio. Compara el resultado con el de dos pequeñas esferas, e interpreta la diferencia.

Ejercicio 2.8

Utilice la ley Gauss para calcular la capacitancia mutua de los siguientes sistemas de dos electrodos, con la sección transversal mostrada en la Fig. 7 (reproducida a la derecha):

(i) una esfera conductora dentro de una cavidad esférica concéntrica en otro conductor, y

(ii) un cilindro conductor largo dentro de una cavidad coaxial en otro conductor, es decir, un cable coaxial. (En este caso, hablamos de la capacitancia por unidad de longitud).

Comparar los resultados con los obtenidos en la Sec. 2.2 utilizando la solución de ecuación de Laplace.

Ejercicio 2.9

Calcular la distribución del potencial electrostático alrededor de dos conductores apenas separados en forma de conos coaxiales y redondos (ver la figura de la derecha), con voltaje\(\ V\) entre ellos. Compare el resultado con el de un problema 2D similar, con los conos reemplazados por cuñas de cara plana. ¿Se pueden calcular las capacidades mutuas entre los conductores en estos sistemas? Si no, ¿puedes estimarlos?

Ejercicio 2.10

Calcular la capacitancia mutua entre dos electrodos rectangulares, planos de área\(\ A=a \times l\), con un pequeño ángulo\(\ \varphi_{0}<<a / \rho_{0}\) entre ellos — ver la figura a la derecha.

Ejercicio 2.11

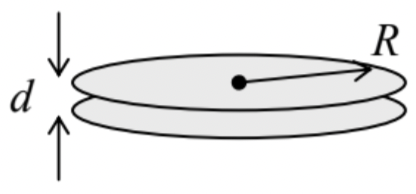
Usando los resultados para un solo disco redondo delgado, obtenidos en la Sec. 4, considere un sistema de dos discos de este tipo a una pequeña\(\ d<<R\) distancia uno del otro;
vea la figura a la derecha. En particular, calcule:

i) la matriz de capacitancia recíproca del sistema,

ii) la capacitancia mutua entre los discos,

(iii) la capacitancia parcial, y

iv) la capacitancia efectiva de un disco,

(todo en la primera aproximación distinta de cero en\(\ d / R<<1\)). Comparar los resultados (ii) - (iv) e interpretar sus
similitudes y diferencias.

Ejercicio 2.12 ^*

Calcular la capacitancia mutua (por unidad de longitud) entre dos conductores cilíndricos formando un sistema con la sección transversal mostrada en la figura de la derecha, en el límite\(\ t<<w<<R\).

Sugerencia: Es posible que te guste usar elíptica (¡no “elipsoidal”!) coordenadas\(\ \{\alpha, \beta\}\) definidas por la siguiente igualdad:

\(\ x+i y=c \cosh (\alpha+i \beta),(*)\)

con la elección adecuada de la constante\(\ c\). En estas coordenadas 2D ortogonales, el operador Laplace es muy sencillo: ⁷⁸

\(\ \nabla^{2}=\frac{1}{c^{2}\left(\cosh ^{2} \alpha-\cos ^{2} \beta\right)}\left(\frac{\partial^{2}}{\partial \alpha^{2}}+\frac{\partial^{2}}{\partial \beta^{2}}\right).\)

Ejercicio 2.13

Formular problemas electrostáticos 2D que puedan resolverse utilizando cada una de las siguientes funciones analíticas de la variable compleja\(\ \boldsymbol{z} \equiv x+i y\):

(i)\(\ \boldsymbol{w}=\ln \boldsymbol{z},\)

ii)\(\ \boldsymbol{w}=\boldsymbol{z}^{1 / 2},\)

y resolver estos problemas.

Ejercicio 2.14

A cada lado de un volumen cilíndrico de sección transversal rectangular\(\ a \times b\), sin cargas eléctricas en su interior, el campo eléctrico es uniforme, normal al plano lateral, y opuesto al del lado opuesto — ver la figura a la derecha. Calcular la distribución del potencial eléctrico dentro del volumen, siempre que la magnitud del campo en los lados verticales sea igual\(\ E\). Sugerir un método practicable para implementar dicha distribución potencial.

Ejercicio 2.15

Completar la solución del problema mostrado en la Fig. 12, calculando la distribución de la carga superficial de los semiplanos. ¿Se puede calcular la capacitancia mutua entre las placas (por unidad de longitud)? Si no, ¿puedes estimarlo?

Ejercicio 2.16 ^*

Se ha cortado una tubería metálica recta, larga, delgada y cilíndrica redonda, a lo largo de su eje, en dos partes iguales; vea la figura a la derecha.

(i) Utilizar el método de mapeo conforme para calcular las distribuciones del potencial electrostático, creado por el voltaje\(\ V\) aplicado entre las dos partes, tanto fuera como dentro de la tubería, y de la carga superficial.

(ii) Calcular la capacitancia mutua entre las mitades de la tubería (por unidad de longitud), tomando en cuenta una pequeña anchura\(\ 2 t<<R\) del corte.

Sugerencias: En la tarea (i), puede usar la siguiente función compleja:

\(\ \boldsymbol{w}=\ln \left(\frac{R+\boldsymbol{z}}{R-\boldsymbol{z}}\right),\)

mientras que en la Tarea (ii), es recomendable utilizar la solución del problema anterior.

Ejercicio 2.17

Resolver Tarea (i) del problema anterior utilizando el método de separación de variables, y comparar los resultados.

Ejercicio 2.18

Utilice el método de separación variable para calcular la distribución de potencial por encima de la superficie plana de un conductor, con una tira de ancho w separada por cortes muy finos, y polarizada con voltaje\(\ V\) — vea la figura a continuación.

Ejercicio 2.19

Ahora se modifica el problema anterior: la parte de corte y tensión polarizada del plano conductor ahora no es una tira, sino un cuadrado con lado w Calcular la distribución de potencial por encima de la superficie del conductor.

Ejercicio 2.20

Cada electrodo de un condensador plano grande se corta en tiras largas de igual ancho w, con espacios muy estrechos entre ellos. Estas tiras se mantienen a potenciales alternos, como se muestra en la figura de la derecha. Utilice el método de separación variable para calcular la distribución del potencial electrostático en el espacio y explorar el límite\(\ w<<d\).

Ejercicio 2.21

Completar el problema del cilindro iniciado en la Sec. 7 (ver Fig. 17), para los casos en que el voltaje de la tapa superior se fija de la siguiente manera:

i)\(\ V=V_{0} J_{1}\left(\xi_{11} \rho / R\right) \sin \varphi\), donde\(\ \xi_{11} \approx 3.832\) es la primera raíz de la función Bessel\(\ J_{1}(\xi)\);

ii)\(\ V=V_{0}=\text { const }\).

Para ambos casos, calcule el campo eléctrico en los centros de los párpados inferior y superior. (Para Tarea (ii), una respuesta que incluya series y/o integrales es aceptable.)

Ejercicio 2.22

Para un sistema infinitamente largo esbozado en la Fig. 21:

(i) calcular y esbozar la distribución del potencial electrostático dentro del sistema para diversos valores de la relación\(\ R / h\), y

ii) simplificar los resultados para el límite\(\ R / h \rightarrow 0\).

Ejercicio 2.23

Utilice el método de separación variable para encontrar la distribución potencial dentro y fuera de una capa esférica delgada de radio\(\ R\), con una distribución de potencial fija:\(\ \phi(R, \theta, \varphi)=V_{0} \sin \theta \cos \varphi\).

Ejercicio 2.24

Un caparazón esférico delgado lleva una carga eléctrica con densidad de área\(\ \sigma=\sigma_{0} \cos \theta\). Calcular la distribución espacial del potencial electrostático y del campo eléctrico, tanto dentro como fuera del caparazón.

Ejercicio 2.25

Utilice el método de separación variable para calcular la distribución de potencial tanto dentro como fuera de una delgada concha esférica de radio\(\ R\), separada con un corte muy delgado, a lo largo del plano central\(\ z=0\), en dos mitades, con voltaje\(\ V\) aplicado entre ellas — ver la figura a la derecha.

Analizar la solución; en particular, comparar el campo en el eje\(\ z\), para\(\ z>R\), con la Ec. (218).

Sugerencia: Es posible que te guste usar la siguiente integral de un polinomio de Legendre con índice impar\(\ l=1,3,5 \ldots=2 n-1\): ⁷⁹

\(\ I_{n} \equiv \int_{0}^{1} P_{2 n-1}(\xi) d \xi=\frac{1}{n !} \cdot\left(\frac{1}{2}\right) \cdot\left(-\frac{3}{2}\right) \cdot\left(-\frac{5}{2}\right) \ldots\left(\frac{3}{2}-n\right) \equiv(-1)^{n-1} \frac{(2 n-3) ! !}{2 n(2 n-2) ! !}.\)

Ejercicio 2.26

Calcular, hasta los términos\(\ O\left(1 / r^{2}\right)\), el campo eléctrico de largo alcance inducido por una esfera conductora dividida y polarizada por voltaje —similar a la discutida en la Sec. 7 (ver Fig. 32) y en el problema anterior, pero con el plano del corte a una\(\ d<R\) distancia arbitraria del centro— ver la figura a la derecha .

Ejercicio 2.27

Un pequeño conductor (en este contexto, generalmente llamado isla de un solo electrón) se coloca entre dos electrodos conductores, con voltaje V aplicado entre ellos. La brecha entre la isla y uno de los electrodos es tan estrecha que los electrones pueden hacer un túnel cuántico-mecánicamente a través de esta “unión” — vea la figura de la derecha. Descuidando las excitaciones térmicas, calcular la carga de equilibrio de la isla en función de\(\ V\).

Pista: Para resolver este problema, no es necesario saber mucho sobre el túnel cuántico mecánico entre conductores, además de que tal tunelización de un electrón, seguida de relajación energética de las excitaciones resultantes, puede considerarse como un solo evento inelástico (disipador de energía). A excitaciones térmicas despreciables, tal evento se produce solo cuando disminuye la energía potencial total del sistema. ⁸⁰

Ejercicio 2.28

El sistema discutido en el problema anterior se generaliza ahora como muestra la figura de la derecha. Si el voltaje\(\ V^{\prime}\) aplicado entre los dos electrodos inferiores es suficientemente grande, los electrones pueden hacer un túnel sucesivamente a través de dos uniones de este sistema (llamado transistor de un solo electrón), transportando corriente continua entre estos electrodos. Despreciando las excitaciones térmicas, calcule la región de los voltajes\(\ V\) y\(\ V^{\prime}\) donde dicha corriente esté completamente suprimida (Coulomb-bloqueado).

Ejercicio 2.29

Utilice el método de carga de imagen para calcular las cargas superficiales completas inducidas en las placas de un condensador plano de voltaje no polarizado muy amplio de espesor\(\ D\) por una carga puntual\(\ q\) separada de uno de los electrodos por distancia\(\ d\).

Ejercicio 2.30

Demostrar la afirmación, hecha en la Sec. 9, de que el problema de contorno 2D mostrado en la figura de la derecha, puede resolverse usando un número finito de cargas de imagen si el ángulo\(\ \beta\) es igual\(\ \pi / n\), donde\(\ n=1,2, \ldots\)

Ejercicio 2.31

Utilice el método de carga de imagen para calcular la energía potencial de la interacción electrostática entre una carga puntual colocada en el centro de una cavidad esférica que había sido tallada dentro de un conductor conectado a tierra, y las paredes de la cavidad. Mirando el resultado, ¿podría obtenerse de una manera (o maneras) más simples?

Ejercicio 2.32

Utiliza el método de las imágenes para encontrar la función de Green del sistema que se muestra en la figura de la derecha, donde la protuberancia en el plano conductor tiene la forma de una semisfera de radio\(\ R\).

Ejercicio 2.33 ^*

Utilizar la inversión esférica, expresada por la Ec. (198), para desarrollar un método iterativo para un cálculo cada vez más preciso de la capacitancia mutua entre dos esferas metálicas similares de radio\(\ R\), con centros separados por distancia\(\ d>2 R\).

Ejercicio 2.34 ^*

Una esfera metálica de radio\(\ R_{1}\), portadora de carga eléctrica\(\ Q\), se coloca dentro de una cavidad esférica de radio\(\ R_{2}>R_{1}\), tallada dentro de otro metal.
Calcular la fuerza eléctrica ejercida sobre la esfera si su centro se desplaza una pequeña\(\ \delta<<R_{1}, R_{2}-R_{1}\) distancia del de la cavidad — ver la figura a la derecha.

Ejercicio 2.35

Dentro de los modelos simples del apantallamiento de campo eléctrico en conductores, discutidos en la Sec. 2.1, analizar el apantallamiento parcial del campo eléctrico de una carga puntual\(\ q\) por un plano, película conductora uniforme de espesor\(\ t<<\lambda\), donde\(\ \lambda\) está (dependiendo de las estadísticas del portador de carga) ya sea el Debye o la longitud de cribado Thomas-Fermi — ver, respectivamente, las ecuaciones (8) o (10). Supongamos que la distancia\(\ d\) entre la carga y la película es mucho mayor que\(\ t\).

Ejercicio 2.36

Sugerir una definición conveniente de la función de Green para problemas electrostáticos 2D y calcularla para:

(i) el espacio libre ilimitado, y

(ii) el espacio libre sobre un plano conductor.

Utilice este último resultado para volver a resolver el Problema 18.

Ejercicio 2.37

Calcular las funciones de Green 2D para los espacios libres:

(i) fuera de un cilindro conductor redondo, y

(ii) dentro de un orificio cilíndrico redondo en un conductor.

Ejercicio 2.38

Resolver Tarea (i) del Problema 16 (ver también Problema 17), usando el método de función de Green.

Ejercicio 2.39

Resolver el problema de límites 2D que se discutió en la Sec. 11 (Fig. 34) utilizando:

(i) el método de diferencia finita, con una malla cuadrada más fina\(\ h=a / 3\), y

ii) el método de separación de variables.

Compare los resultados en los puntos de malla y comente.

---

Referencia

⁷⁹ Como recordatorio, el operador factorial doble (también llamado “semifactorial”) (!!) es similar al operador factorial habitual (!) , pero con el producto limitado a números de la misma paridad que su argumento —en nuestro caso particular, de los números impares en el numerador, y números pares en el denominador.

⁸⁰ Estrictamente hablando, este modelo, que implica una coherencia cuántica-mecánica insignificante de los eventos de tunelización, es correcto solo si la transparencia de la unión es suficientemente baja, de manera que su resistencia eléctrica efectiva es mucho mayor que la unidad cuántica de resistencia (ver, por ejemplo, QM Sec. 3.2), \(\ R_{\mathrm{Q}} \equiv \pi \hbar / 2 e^{2} \approx 6.5 \mathrm{k} \Omega\)— que se puede hacer fácilmente en el experimento.