8.9: Radiación de dipolo magnético y cuadrupolo eléctrico

A lo largo de este capítulo, hemos visto cuántos resultados importantes se pueden obtener de la Ec. (26) para la radiación dipolar eléctrica por una fuente de pequeño tamaño (Fig. 1). Sólo en casos raros cuando esta radiación está ausente, por ejemplo, si el momento dipolar p de la fuente es igual a cero (o no cambia en el tiempo —ya sea en absoluto o a la frecuencia de nuestro interés), los efectos de orden superior pueden ser importantes. Voy a discutir los dos principales de ellos, la radiación eléctrica cuadrupolo y la radiación magnética dipolo.

En la Sec. 2 anterior, la radiación dipolo eléctrico se calculó tapando la expansión (19) en la fórmula exacta (17b) para el potencial vectorial retardado\(\ \mathbf{A}(\mathbf{r}, t)\). Hagamos un cálculo más exacto, manteniendo también el segundo término de esa expansión:

\[\ \mathbf{j}\left(\mathbf{r}^{\prime}, t-\frac{R}{\nu}\right) \approx \mathbf{j}\left(\mathbf{r}^{\prime}, t-\frac{r}{\nu}+\frac{\mathbf{r}^{\prime} \cdot \mathbf{n}}{\nu}\right) \equiv \mathbf{j}\left(\mathbf{r}^{\prime}, t^{\prime}+\frac{\mathbf{r}^{\prime} \cdot \mathbf{n}}{\nu}\right), \quad \text { where } t^{\prime} \equiv t-\frac{r}{\nu}.\tag{8.130}\]

Dado que la expansión solo es válida si el último término en el argumento de tiempo de\(\ \mathbf{j}\) es relativamente pequeño, en la expansión Taylor de\(\ \mathbf{j}\) con respecto a ese argumento podemos mantener solo dos términos principales:

\[\ \mathbf{j}\left(\mathbf{r}^{\prime}, t^{\prime}+\frac{\mathbf{r}^{\prime} \cdot \mathbf{n}}{\nu}\right) \approx \mathbf{j}\left(\mathbf{r}^{\prime}, t^{\prime}\right)+\frac{\partial \mathbf{j}\left(\mathbf{r}^{\prime}, t^{\prime}\right)}{\partial t^{\prime}} \frac{\left(\mathbf{r}^{\prime} \cdot \mathbf{n}\right)}{\nu},\tag{8.131}\]

de manera que la Ec. (17b) rinde\(\ \mathbf{A}=\mathbf{A}_{d}+\mathbf{A}^{\prime}\), donde\(\ \mathbf{A}_{\mathrm{d}}\) está la contribución del dipolo eléctrico dada por la ecuación (23), y\(\ \mathbf{A} \text {' }\) es el nuevo término del siguiente orden en el parámetro pequeño\(\ r^{\prime}<<r\):

\[\ \mathbf{A}^{\prime}(\mathbf{r}, t)=\frac{\mu}{4 \pi r \nu} \frac{\partial}{\partial t^{\prime}} \int \mathbf{j}\left(\mathbf{r}^{\prime}, t^{\prime}\right)\left(\mathbf{r}^{\prime} \cdot \mathbf{n}\right) d^{3} r^{\prime}.\tag{8.132}\]

Así como se hizo en la Sec. 2, evaluemos este término para un sistema de partículas no relativistas con cargas eléctricas\(\ q_{k}\) y radio-vectores\(\ \mathbf{r}_{k}(t)\):

\[\ \mathbf{A}^{\prime}(\mathbf{r}, t)=\frac{\mu}{4 \pi r \nu}\left[\frac{d}{d t} \sum_{k} q_{k} \dot{\mathbf{r}}_{k}\left(\mathbf{r}_{k} \cdot \mathbf{n}\right)\right]_{t=t^{\prime}}.\tag{8.133}\]

Usando nuevamente la identidad “bac menos cab” del álgebra vectorial, ⁴⁸ el operando vectorial de la ecuación (133) puede reescribirse como

\ [\\ comenzar {alineado}
\ punto {\ mathbf {r}} _ {k}\ izquierda (\ mathbf {r} _ {k}\ cdot\ mathbf {n}\ derecha) &\ equiv\ frac {1} {2}\ punto {\ mathbf {r}} _ {k}\ izquierda (\ mathbf {r} _ {k}\ cdot\ mathbf {n}\ derecha) +\ frac {1} {2}\ punto {\ mathbf {r}} _ {k}\ izquierda (\ mathbf {n}\ cdot\ mathbf {r} _ _ {k}\ derecha) =\ frac {1} {2}\ izquierda (\ mathbf {r} _ _ {k}\ veces\ punto {\ mathbf {r}} _ {k}\ derecha)\ veces\ mathbf {n} +\ frac {1} {2}\ mathbf {r} _ _ {k}\ izquierda (\ mathbf {n}\ cdot\ punto {\ mathbf {r}} _ {k}\ derecha) +\ frac {1} {2}\ punto {\ mathbf {r} _ {k}\ izquierda (\ mathbf {n}\ cdot\ mathbf {r} _ {k}\ derecha)\\
&\ equiv\ frac {1} {2}\ izquierda (\ mathbf {r} _ {k}\ veces\ punto {\ mathbf {r}} _ {k}\ derecha)\ veces\ mathbf {n} +\ frac {1} {2}\ frac {d} {d t}\ izquierda [\ mathbf {r} _ {k}\ izquierda (\ mathbf {n}\ cdot\ mathbf {r} _ {k}\ derecha)\ derecha],
\ end {alineado}\ tag {8.134}\]

de manera que el lado derecho de la ecuación (133) pueda representarse como una suma de dos términos,\(\ \mathbf{A}^{\prime}=\mathbf{A}_{\mathrm{m}}+\mathbf{A}_{\mathrm{q}}\), donde

\[\ \mathbf{A}_{\mathrm{m}}(\mathbf{r}, t)=\frac{\mu}{4 \pi r \nu} \dot{\mathbf{m}}\left(t^{\prime}\right) \times \mathbf{n} \equiv \frac{\mu}{4 \pi r \nu} \dot{\mathbf{m}}\left(t-\frac{r}{\nu}\right) \times \mathbf{n}, \quad \text { with } \mathbf{m}(t) \equiv \frac{1}{2} \sum_{k} \mathbf{r}_{k}(t) \times q_{k} \dot{\mathbf{r}}_{k}(t);\tag{8.135}\]

\[\ \mathbf{A}_{\mathrm{q}}(\mathbf{r}, t)=\frac{\mu}{8 \pi r \nu}\left[\frac{d^{2}}{d t^{2}} \sum_{k} q_{k} \mathbf{r}_{k}\left(\mathbf{n} \cdot \mathbf{r}_{k}\right)\right]_{t=t^{\prime}}.\tag{8.136}\]

Comparando la segunda de Eqs. (135) con la Eq. (5.91), vemos que m es solo el momento magnético total de la fuente. Por otro lado, la primera de las Ecuaciones (135) es absolutamente similar en estructura a la Ecuación (23), con p reemplazada por\(\ (\mathbf{m} \times \mathbf{n}) / \nu\), de manera que para el componente correspondiente del campo magnético da (en la misma aproximación\(\ r >> \lambda\)) un resultado similar a la Ec. (24):

\[\ \text{Magnetic dipole radiation: field}\quad\quad\quad\quad \mathbf{B}_{\mathrm{m}}(\mathbf{r}, t)=\frac{\mu}{4 \pi r \nu} \nabla \times\left[\dot{\mathbf{m}}\left(t-\frac{r}{\nu}\right) \times \mathbf{n}\right]=-\frac{\mu}{4 \pi r \nu^{2}} \mathbf{n} \times\left[\ddot{\mathbf{m}}\left(t-\frac{r}{\nu}\right) \times \mathbf{n}\right].\tag{8.137}\]

Según esta expresión, al igual que en la radiación dipolo eléctrico, el vector B es perpendicular al vector n, y su magnitud también es proporcional a\(\ \sin \Theta\), donde\(\ \Theta\) está ahora el ángulo entre la dirección hacia el punto de observación y la segunda vez derivada del vector m — en lugar de p:

\[\ B_{\mathrm{m}}=\frac{\mu}{4 \pi r \nu^{2}} \ddot{m}\left(t-\frac{r}{\nu}\right) \sin \Theta.\tag{8.138}\]

Como resultado, la intensidad de esta radiación dipolo magnético tiene una distribución angular similar:

\[\ \text{Magnetic dipole radiation: power}\quad\quad\quad\quad S_{r}=Z H^{2}=\frac{Z}{\left(4 \pi \nu^{2} r\right)^{2}}\left[\ddot{m}\left(t-\frac{r}{\nu}\right)\right]^{2} \sin ^{2} \Theta\tag{8.139}\]

- cf. Ec. (26), además del significado (generalmente) diferente del ángulo\(\ \Theta\).

Tenga en cuenta, sin embargo, que esta radiación suele ser mucho más débil que su contraparte eléctrico-dipolo. Por ejemplo, para una partícula no relativista con carga eléctrica\(\ q\), moviéndose sobre una trayectoria de tamaño lineal\(\ \sim a\), el momento dipolo eléctrico es del orden de\(\ qa\), mientras que su momento magnético escala como\(\ q a^{2} \omega\), dónde\(\ \omega\) está la frecuencia de movimiento. Como resultado, la relación de las intensidades de radiación dipolo magnético y eléctrico es del orden de\(\ (a \omega / \nu)^{2}\), es decir, la relación cuadrada de la velocidad de la partícula a la velocidad de las ondas emitidas, que tiene que ser mucho menor que 1 para que nuestro cálculo no relativista sea válido.

La distribución angular de la radiación cuadrupolar eléctrica, descrita por la Ec. (136), es más complicada. Para mostrar esto, podemos agregar a\(\ \mathbf{A}_{\mathrm{q}}\) un vector paralelo a n (es decir, a lo largo de la propagación de la onda), obteniendo

\[\ \mathbf{A}_{\mathrm{q}}(\mathbf{r}, t) \rightarrow \frac{\mu}{24 \pi r \nu} \ddot{\mathscr{Q}}\left(t-\frac{r}{\nu}\right), \quad \text { where } \mathscr{Q} \equiv \sum_{k} q_{k}\left\{3 \mathbf{r}_{k}\left(\mathbf{n} \cdot \mathbf{r}_{k}\right)-\mathbf{n} r_{k}^{2}\right\},\tag{8.140}\]

porque esta adición no da ninguna contribución a la componente transversal de los campos eléctrico y magnético, es decir, a la onda radiada. De acuerdo con la definición anterior del vector\(\ \mathscr{Q}\), sus componentes cartesianos pueden representarse como

\[\ \mathscr{Q}_{j}=\sum_{j^{\prime}=1}^{3} \mathscr{Q}_{j j^{\prime}} n_{j^{\prime}},\tag{8.141}\]

donde\(\ \mathscr{Q}_{j j’}\) están los elementos del tensor cuadrupolo eléctrico del sistema — ver el último de las ecuaciones (3.4):

\[\ \mathscr{Q}_{j j^{\prime}}=\sum_{k} q_{k}\left(3 r_{j} r_{j^{\prime}}-r^{2} \delta_{j j^{\prime}}\right)_{k}.\tag{8.142}\]

(Permítanme esperar que el lector ya haya adquirido alguna experiencia en el cálculo de los componentes de este tensor —por ejemplo, para los sistemas simples especificados en los Problemas 3.2 y 3.3.) Ahora tomando el rizo de la primera de Eqs. (140) a\(\ r >> \lambda\), obtenemos

\[\ \mathbf{B}_{\mathrm{q}}(\mathbf{r}, t)=-\frac{\mu}{24 \pi r \nu^{2}} \mathbf{n} \times \dddot{\mathscr{Q}}\left(t-\frac{r}{\nu}\right).\quad\quad\quad\quad\text{Electric quadrupole radiation: field}\tag{8.143}\]

Esta expresión es similar a las ecuaciones (24) y (137), pero según las ecuaciones (140) y (142), los componentes del vector\(\ \mathscr{Q}\) sí dependen de la dirección del vector n, conduciendo a una dependencia angular diferente de\(\ S_{r}\).

Como ejemplo más simple, consideremos el sistema de dos cargas eléctricas de igual punto que se mueven simétricamente, a distancias iguales\(\ d(t)<<\lambda\) de un centro estacionario — ver Fig. 16.

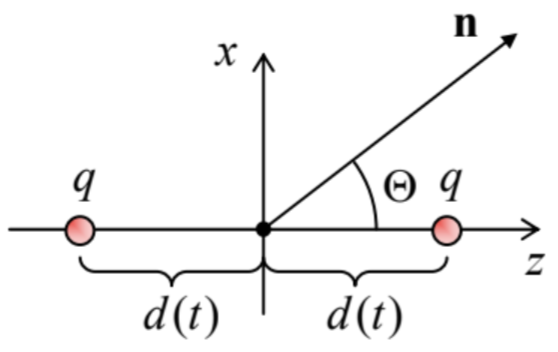Fig. 8.16. El sistema más simple que emite radiación eléctrica cuadrupolo.

Debido a la simetría del sistema, sus momentos dipolares p y m (y de ahí su radiación dipolar eléctrica y magnética) desaparecen, pero el tensor cuadrupolo (142) todavía tiene componentes distintos de cero. Con la elección de coordenadas que se muestra en la Fig. 16, estos componentes son diagonales:

\[\ \mathscr{Q}_{x x}=\mathscr{Q}_{y y}=-2 q d^{2}, \quad \mathscr{Q}_{z z}=4 q d^{2}.\tag{8.144}\]

Con el eje x seleccionado dentro del plano común del eje z y la dirección n hacia la fuente (Fig. 16), de manera que\(\ n_{x}=\sin \Theta\), y\(\ n_{y}=0\)\(\ n_{z}=\cos \Theta\), la Eq. (141) rinde

\[\ \mathscr{Q}_{x}=-2 q d^{2} \sin \Theta, \quad \mathscr{Q}_{y}=0, \quad \mathscr{Q}_{z}=4 q d^{2} \cos \Theta,\tag{8.145}\]

y el producto vector en la Ec. (143) tiene solo un componente cartesiano que no desaparece:

\[\ (\mathbf{n} \times \dddot{\mathscr{Q}})_{y}=n_{z} \dddot{\mathscr{Q}}_{x}-n_{x} \ddot{\mathscr{Q}}_{z}=-6 q \sin \Theta \cos \Theta \frac{d^{3}}{d t^{3}}\left[d^{2}(t)\right].\tag{8.146}\]

Como resultado, la intensidad de radiación cuadrupolo,\(\ S \propto B_{\mathrm{q}}^{2}\), es proporcional a\(\ \sin ^{2} \Theta \cos ^{2} \Theta\), es decir, desaparece no solo a lo largo del eje de simetría del sistema (como harían las radiaciones dipolo eléctrico y dipolo magnético), sino también en todas las direcciones perpendiculares a este eje, alcanzando sus máximos en\(\ \Theta=\pm \pi / 4\) .

Para sistemas más complejos, la distribución angular de la radiación cuadripolar eléctrica puede ser diferente, pero se puede demostrar que su potencia total (instantánea) siempre obedece a la siguiente fórmula simple:

\[\ \text{Electric quadrupole radiation: power}\quad\quad\quad\quad \mathscr{P}_{q}=\frac{Z}{1440 \pi \nu^{4}} \sum_{j, j^{\prime}=1}^{3}\left(\mathscr{\dddot{Q}}_{j j^{\prime}}\right)^{2}.\tag{8.147}\]

Permítanme terminar esta sección dando, también sin pruebas, un dato más importante para algunas aplicaciones: debido a su diferente estructura espacial, los campos de radiación magnético-dipolo y cuadrupolo eléctrico no interfieren, es decir, la potencia total de la radiación (descuidando el dipolo eléctrico y el multipolo superior términos) se pueden encontrar como la suma de estos componentes, calculados de forma independiente. Por el contrario, si las radiaciones dipolo eléctrico y dipolo magnético del mismo sistema son comparables, típicamente interfieren coherentemente, de manera que sus campos de radiación (en lugar de potencias) deben resumirse.

---

Referencia

⁴⁸ Si aún lo necesitas, consulta MA Eq. (7.5).