13.5: Adición relativista de velocidades

Objetivos de aprendizaje

Al final de esta sección, podrás:

• Calcular la suma de velocidad relativista.
• Explique cuándo se debe usar la adición de velocidad relativista en lugar de la adición clásica de velocidades.
• Calcular el desplazamiento Doppler relativista.

Si alguna vez has visto que un kayak se mueve por un río de rápido movimiento, sabes que quedarte en el mismo lugar sería difícil. La corriente del río tira el kayak a lo largo. Empujar los remos hacia atrás contra el agua puede mover el kayak hacia adelante en el agua, pero eso solo representa parte de la velocidad. El movimiento del kayak es un ejemplo de adición clásica de velocidades. En la física clásica, las velocidades se suman como vectores. La velocidad del kayak es la suma vectorial de su velocidad relativa al agua y la velocidad del agua en relación con la orilla del río.

Figura\(\PageIndex{1}\): La velocidad total de un kayak, como este en el río Deerfield en Massachusetts, es su velocidad relativa al agua así como la velocidad del agua en relación con la orilla del río. (crédito: abkfenris, Flickr)

Adición de velocidad clásica

Por simplicidad, restringimos nuestra consideración de la adición de velocidad al movimiento unidimensional. Clásicamente, las velocidades se suman como números regulares en movimiento unidimensional (Figura\(\PageIndex{1}\)). Supongamos, por ejemplo, que una niña está montando en un trineo a una velocidad de 1.0 m/s con respecto a un observador. Ella lanza una bola de nieve primero hacia adelante, luego hacia atrás a una velocidad de 1.5 m/s con relación al trineo. Denotamos dirección con signos más y menos en una dimensión; en este ejemplo, adelante es positivo. \(v\)Sea la velocidad del trineo en relación con la Tierra, la velocidad de\(u\) la bola de nieve en relación con el observador con destino a la Tierra, y\(u'\) la velocidad de la bola de nieve en relación con el trineo.

Figura\(\PageIndex{2}\): Clásicamente, las velocidades se suman como números ordinarios en movimiento unidimensional. Aquí la niña lanza una bola de nieve hacia adelante y luego hacia atrás desde un trineo. La velocidad del trineo en relación con la Tierra es\(v = 1.0 \, m/s\). La velocidad de la bola de nieve en relación con el camión es\(u'\), mientras que su velocidad relativa a la Tierra es\(u\). Clásicamente,\(u = v + u'\).

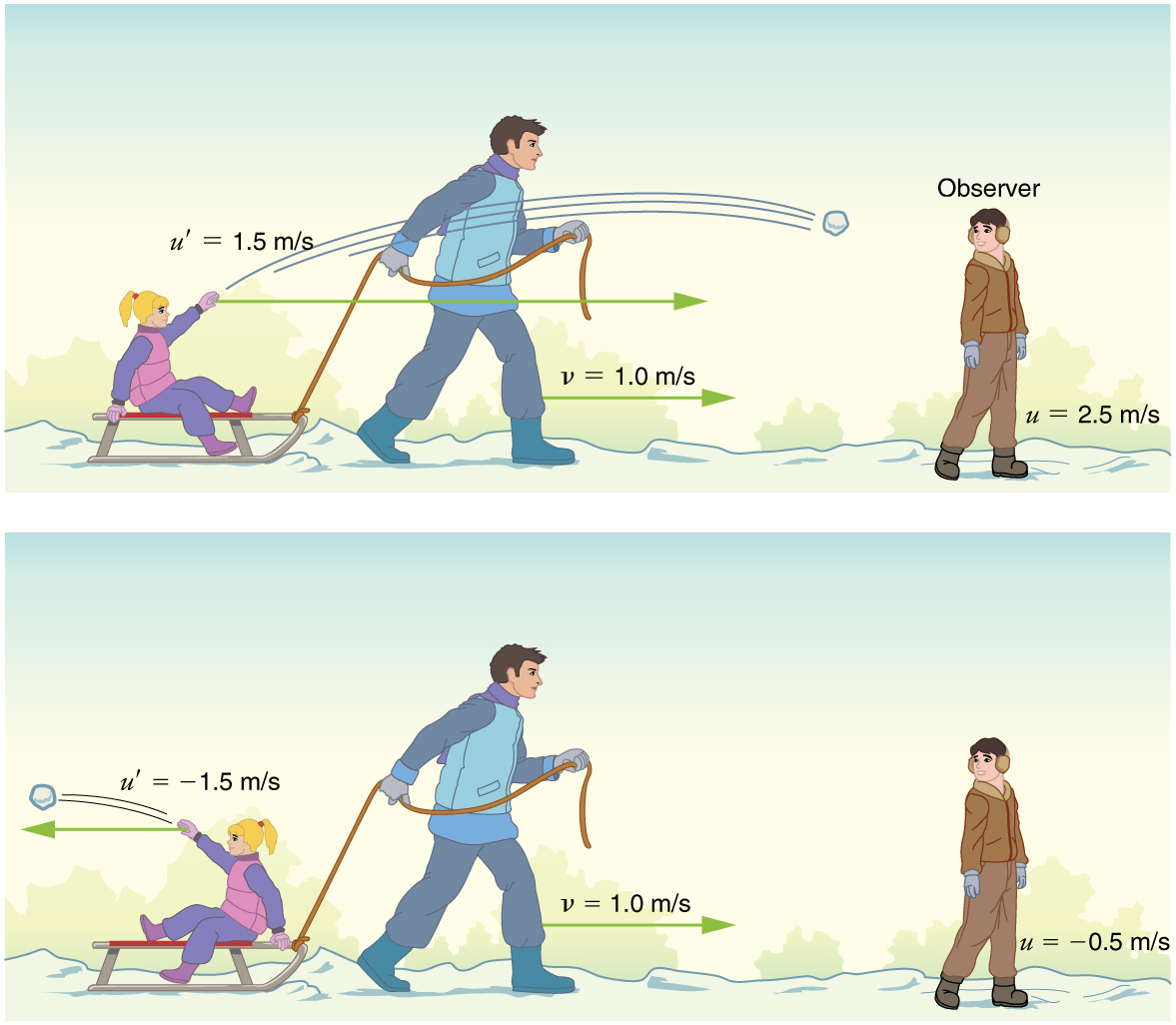
Adición de velocidad clásica

\[u = v + u'\]

Así, cuando la niña lanza la bola de nieve hacia adelante,\(U = 1.0 \, m/s + 1.5 \, m/s = 2.5 \, m/s\). Tiene sentido intuitivo que la bola de nieve se dirija más rápido hacia el observador con destino a la Tierra, porque es arrojada hacia adelante desde un vehículo en movimiento. Cuando la niña lanza la bola de nieve hacia atrás,\(u = 1.0 \, m/s + (-1.5 \, m/s) = -0.5 \, m/s\). El signo menos significa que la bola de nieve se aleja del observador con destino a la Tierra.

Adición de velocidad relativista

El segundo postulado de la relatividad (verificado por una extensa observación experimental) dice que la adición clásica de velocidad no se aplica a la luz. Imagínese un automóvil viajando de noche por una carretera recta, como en la Figura\(\PageIndex{3}\). Si la adición de velocidad clásica se aplicara a la luz, entonces la luz de los faros del automóvil se acercaría al observador en la acera a una velocidad\(u = v + c\). Pero sabemos que la luz se alejará del automóvil a una velocidad\(c\) relativa al conductor del automóvil, y la luz también se moverá hacia el observador en la acera a velocidad\(c\).

\(\PageIndex{3}\)Figura:Según el experimento y el segundo postulado de la relatividad, la luz de los faros del automóvil se aleja del auto a velocidad y\(c\) hacia el observador en la acera a velocidad.\(c\) La adición de velocidad clásica no es válida.

Adición de velocidad relativista

O la luz es una excepción, o la fórmula clásica de adición de velocidad solo funciona a bajas velocidades. Este último es el caso. La fórmula correcta para la adición de velocidad relativista unidimensional es

\[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}},\]

donde\(v\) es la velocidad relativa entre dos observadores,\(u\) es la velocidad de un objeto con respecto a un observador, y\(u'\) es la velocidad relativa al otro observador. (Para facilitar la visualización, a menudo elegimos medir\(u\) en nuestro marco de referencia, mientras que alguien que se mueve en\(v\) relativo a nosotros mide\(u'\).) Tenga en cuenta que el término\(\frac{vu'}{c^2}\) se vuelve muy pequeño a bajas velocidades, y\(u = \frac{v + u}{1 + \frac{vu'}{v^2}}\) da un resultado muy cercano a la adición de velocidad clásica. Como antes, vemos que la adición de velocidad clásica es una excelente aproximación a la fórmula relativista correcta para velocidades pequeñas. No es de extrañar que parezca correcto en nuestra experiencia.

Ejemplo\(\PageIndex{1}\): Showing that the Speed of Light towards an Observer is Constant (in a Vacuum): The Speed of Light is the Speed of Light

Supongamos que una nave espacial que se dirige directamente hacia la Tierra a la mitad de la velocidad de la luz nos envía una señal en un haz de luz producido por láser. Dado que la luz sale de la nave a la velocidad observada desde la nave, calcula la velocidad a la que se acerca a la Tierra.

Figura\(\PageIndex{4}\)

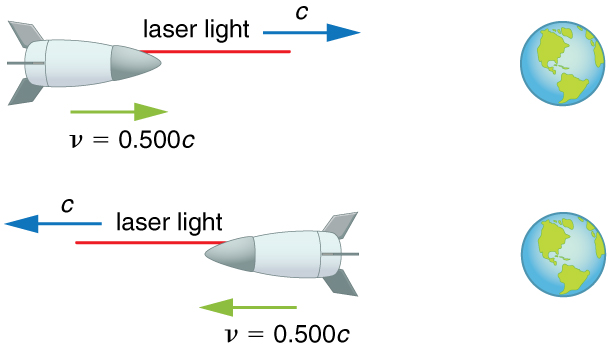
Estrategia

Debido a que la luz y la nave espacial se mueven a velocidades relativistas, no podemos usar una simple adición de velocidad. En cambio, podemos determinar la velocidad a la que la luz se acerca a la Tierra usando la adición de velocidad relativista.

Solución

1. Identificar los conocimientos:\(v = 0.500 c\);\(u' = c\)
2. Identificar lo desconocido:\(u\)
3. Elija la ecuación apropiada:\(u = \frac{v + u'}{1 + \frac{vu'}{c^2}}\).
4. Enchufa los conocimientos en la ecuación. \[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} = \dfrac{0.500 c + c}{1 + \frac{(0.500C)(c)}{c^2}} = \dfrac{(0.500 +1)c}{1 + \frac{0.500c^2}{c^2}} = \dfrac{1.500 c}{1 + 0.500} = \dfrac{1.500c}{1.500} + c\]

Discusión

La adición de velocidad relativista da el resultado correcto. La luz sale del barco a gran velocidad

y se acerca a la Tierra a gran velocidad\(c\). La velocidad de la luz es independiente del movimiento relativo de la fuente y el observador, ya sea que el observador esté en la nave o con destino a la Tierra.

Las velocidades no pueden sumar a mayores que la velocidad de la luz, siempre que\(v\) sea menor\(c\) y no\(u'\) exceda\(c\). El siguiente ejemplo ilustra que la adición de velocidad relativista no es tan simétrica como la adición de velocidad clásica.

Ejemplo\(\PageIndex{2}\): Comparing the Speed of Light towards and away from an Observer: Relativistic Package Delivery

Supongamos que la nave espacial en el ejemplo anterior se acerca a la Tierra a la mitad de la velocidad de la luz y dispara un bote a una velocidad de\(0.750 c\).

1. ¿A qué velocidad verá el bote un observador con destino a la Tierra si se dispara directamente hacia la Tierra?
2. ¿Si se dispara directamente lejos de la Tierra? (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\)

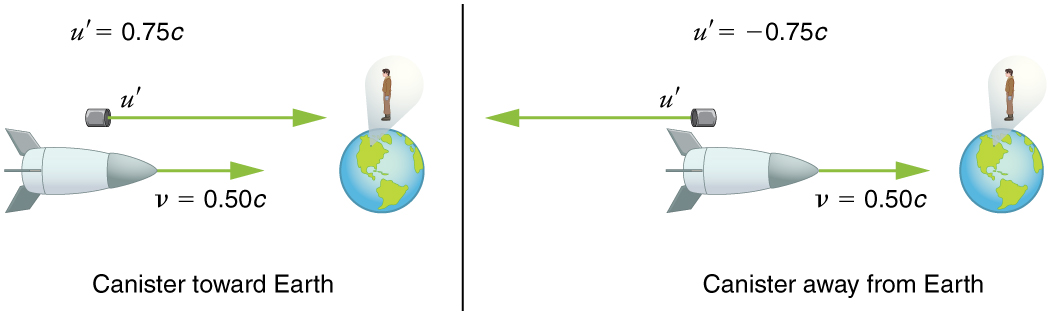
Estrategia

Debido a que el bote y la nave espacial se mueven a velocidades relativistas, debemos determinar la velocidad del bote por un observador terrestre utilizando la adición de velocidad relativista en lugar de una simple adición de velocidad.

Solución para (a)

1. Identificar los conocimientos:\(v = 0.500 c\);\(u' = 0.750 c\)
2. Identificar lo desconocido:\(u\)
3. Elija la ecuación apropiada:\(u = \frac{v + u'}{1 + \frac{vu'}{c^2}}\)
4. Enchufa los conocimientos en la ecuación:\[ u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} = \dfrac{0.500 c + 0.750 c}{1 + \frac{(0.500 c)(0.750 c)}{c^2}} = \dfrac{1.250 c}{1 + 0.375)} = 0.909 c\]

Solución para (b)

1. Identificar los conocimientos:\(v = 0.500 c\);\(u' = -0.750 c\)
2. Identificar lo desconocido:\(u\)
3. Elija la ecuación apropiada:\(u = \frac{v + u'}{1 + \frac{vu'}{c^2}}\)
4. Enchufa los conocimientos en la ecuación:\[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} = \dfrac{0.500 c + (-0.750 c)}{1 + \frac{(0.500 C)(-0.750 c)}{c^2}} = \dfrac{-0.250 c}{1 - 0.375} = -0.400 c\]

Discusión

El signo menos indica velocidad alejándose de la Tierra (en dirección opuesta a\(v\)), lo que significa que el bote se dirige hacia la Tierra en la parte (a) y lejos en la parte (b), como se esperaba. Pero las velocidades relativistas no agregan tan simples como lo hacen clásicamente. En la parte (a), el bote sí se acerca a la Tierra más rápido, pero no a la simple suma de\(1.250 c\). La velocidad total es menor de lo que obtendrías clásicamente. Y en la parte (b), el bote se aleja de la Tierra a una velocidad de\(-0.400c\), que es más rápida de\(-0.250 c\) lo que cabría esperar clásicamente. Las velocidades ni siquiera son simétricas. En la parte (a) el bote se mueve\(0.409 c\) más rápido que el barco en relación con la Tierra, mientras que en la parte (b) se mueve\(0.900 c\) más lento que el barco.

Desplazamiento Doppler

Aunque la velocidad de la luz no cambia con la velocidad relativa, las frecuencias y longitudes de onda de la luz sí lo hacen. Primero discutido para las ondas sonoras, se produce un desplazamiento Doppler en cualquier onda cuando hay movimiento relativo entre la fuente y el observador.

EFECTO DOPPLER RELATIVISTA

La longitud de onda observada de la radiación electromagnética es más larga (llamada desplazamiento al rojo) que la emitida por la fuente cuando la fuente se aleja del observador y más corta (llamada desplazamiento azul) cuando la fuente se mueve hacia el observador.

\[\lambda_{obs} = \lambda_s \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}}\]

En la ecuación Doppler\(\lambda_{obs}\) está la longitud de onda observada,\(\lambda_s\) es la longitud de onda fuente, y\(u\) es la velocidad relativa de la fuente al observador. La velocidad\(u\) es positiva para el movimiento que se aleja de un observador y negativa para el movimiento hacia un observador. En términos de frecuencia fuente y frecuencia observada, esta ecuación puede escribirse\[f_{obs} = f_s \sqrt{\dfrac{1 - \frac{u}{c}}{1 + \frac{u}{c}}}.\] Observe que los signos — y + son diferentes que en la ecuación de longitud de onda.

CONEXIÓN CARRERA: Astr

Si te interesa una carrera que requiera un conocimiento de relatividad especial, probablemente no haya mejor conexión que la astronomía. Los astrónomos deben tener en cuenta los efectos relativistas cuando calculan distancias, tiempos y velocidades de agujeros negros, galaxias, cuásares y todos los demás objetos astronómicos. Para tener una carrera en astronomía, se necesita al menos una licenciatura en física o astronomía, pero a menudo se requiere una maestría o doctorado. También se necesita una buena formación en matemáticas de alto nivel.

Ejemplo\(\PageIndex{3}\): Calculating a Doppler Shift: Radio Waves from a Receding Galaxy

Supongamos que una galaxia se aleja de la Tierra a una velocidad\(0.825 c\). Emite ondas de radio con una longitud de onda de\(0.525 \, m\).

¿Qué longitud de onda detectaríamos en la Tierra?

Estrategia

Debido a que la galaxia se mueve a una velocidad relativista, debemos determinar el desplazamiento Doppler de las ondas de radio utilizando el desplazamiento Doppler relativista en lugar del desplazamiento Doppler clásico.

Solución

1. Identificar los conocimientos:\(u = 0.825 c\);\(\lambda_s = 0.525 \, m\)
2. Identificar lo desconocido:\(\lambda_{obs}\)
3. Elija la ecuación apropiada:\(\lambda_{obs} = \lambda \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}}\)
4. Enchufa los conocimientos en la ecuación\[\lambda_{obs} = \lambda \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}} = (0.525 \, m)\sqrt{\dfrac{1 + \frac{0.825 c}{c}}{1 - \frac{0.825 c}{c}}} = 1.70 \, m.\]

Discusión

Debido a que la galaxia se está alejando de la Tierra, esperamos que las longitudes de onda de radiación que emite se desplacen al rojo. La longitud de onda que calculamos es de 1.70 m, que está desplazada al rojo de la longitud de onda original de 0.525 m.

El desplazamiento Doppler relativista es fácil de observar. Esta ecuación tiene aplicaciones cotidianas que van desde mediciones de velocidad de radar de transporte con desplazamiento Doppler hasta monitoreo de tormentas por radar Doppler. En observaciones astronómicas, el desplazamiento Doppler relativista proporciona información de velocidad como el movimiento y la distancia de las estrellas.

Ejercicio\(\PageIndex{1}\)

Supongamos que una sonda espacial se aleja de la Tierra a una velocidad\(0.350 c\). Envía un mensaje de ondas de radio de vuelta a la Tierra a una frecuencia de 1.50 GHz. ¿Con qué frecuencia se recibe el mensaje en la Tierra?

Responder

\[f_{obs} = f_c \sqrt{\dfrac{1 - \frac{u}{c}}{1 + \frac{u}{c}}} = (1.50 \, GHz) \sqrt{\dfrac{1 - \frac{0.350 c}{c}}{1 + \frac{0.350 c}{c}}} = 1.04 \, GHz \nonumber\]

Resumen

• Con la adición de velocidad clásica, las velocidades se suman como números regulares en movimiento unidimensional:\(u = v + u'\), donde\(v\) está la velocidad entre dos observadores,\(u\) es la velocidad de un objeto en relación con un observador, y\(u'\) es la velocidad relativa al otro observador.
• Las velocidades no pueden sumar para ser mayores que la velocidad de la luz. La adición de velocidad relativista describe las velocidades de un objeto que se mueve a una velocidad relativista:\[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} \nonumber\]
• Un observador de radiación electromagnética ve efectos Doppler relativistas si la fuente de la radiación se mueve en relación con el observador. La longitud de onda de la radiación es más larga (llamada desplazamiento al rojo) que la emitida por la fuente cuando la fuente se aleja del observador y más corta (llamada desplazamiento azul) cuando la fuente se mueve hacia el observador. La longitud de onda desplazada se describe por la ecuación\[\lambda_{obs} = \lambda_s \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}} \nonumber\]\(\lambda_{obs}\) es la longitud de onda observada,\(\lambda_s\) es la longitud de onda de la fuente, y\(u\) es la velocidad relativa de la fuente al observador.

Glosario

adición de velocidad clásica

el método de sumar velocidades cuando\(v << c\), las velocidades se suman como números regulares en movimiento unidimensional:\(u = v + u'\), donde\(v\) está la velocidad entre dos observadores,\(u\) es la velocidad de un objeto en relación con un observador, y\(u'\) es la velocidad relativa al otro observador.

adición de velocidad relativista

el método de agregar velocidades de un objeto que se mueve a una velocidad relativista\(u \frac{v + u'}{1 + \frac{vu'}{c^2}}\), donde\(v\) es la velocidad relativa entre dos observadores,\(u\) es la velocidad de un objeto en relación con un observador, y\(u'\) es la velocidad relativa al otro observador

efectos Doppler relativistas

un cambio en la longitud de onda de la radiación que se mueve en relación con el observador; la longitud de onda de la radiación es más larga (llamada desplazamiento al rojo) que la emitida por la fuente cuando la fuente se aleja del observador y más corta (llamada desplazamiento azul) cuando la fuente se mueve hacia el observador; la desplazada longitud de onda se describe por la ecuación\[\lambda_{obs} = \lambda_s \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}}\] donde\(\lambda_{obs}\) es la longitud de onda observada,\(\lambda_s\) es la longitud de onda fuente, y\(u\) es la velocidad de la fuente al observador