13.6: Momentum relativista
- Page ID
- 133842
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
Al final de esta sección, podrás:
- Calcular el impulso relativista.
- Explique por qué la única masa de la que tiene sentido hablar es la masa de descanso.
En la física clásica, el impulso es un producto simple de la masa y la velocidad. No obstante, vimos en el último apartado que cuando se toma en cuenta la relatividad especial, los objetos masivos tienen un límite de velocidad. ¿Qué efecto crees que tienen la masa y la velocidad en el impulso de los objetos que se mueven a velocidades relativistas?

El impulso es uno de los conceptos más importantes en física. La forma más amplia de la segunda ley de Newton se afirma en términos de impulso. El impulso se conserva siempre que la fuerza externa neta en un sistema sea cero. Esto hace que la conservación del impulso sea una herramienta fundamental para analizar colisiones. Todo el Trabajo, Energía y Recursos Energéticos está dedicado al impulso, y el impulso también ha sido importante para muchos otros temas, particularmente donde hubo colisiones involucradas. Veremos que el impulso tiene la misma importancia en la física moderna. El impulso relativista se conserva, y gran parte de lo que sabemos sobre la estructura subatómica proviene del análisis de colisiones de partículas relativistas producidas por aceleradores.
El primer postulado de la relatividad establece que las leyes de la física son las mismas en todos los marcos inerciales. ¿La ley de conservación del impulso sobrevive a este requisito a altas velocidades? La respuesta es sí, siempre que el impulso se defina de la siguiente manera.
Definición: Momentum relativista
El impulso relativista\(p\) es el impulso clásico multiplicado por el factor relativista\(\gamma\)
\[p = \gamma mu,\]
donde\(m\) es la masa de reposo del objeto,\(u\) es su velocidad relativa a un observador, y el factor relativista
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}}.\]
Tenga en cuenta que aquí usamos\(u\) para la velocidad para distinguirla de la velocidad relativa\(v\) entre observadores. Aquí sólo se está considerando a un observador. Con\(p\) definido de esta manera, el impulso total\(p_{tot}\) se conserva siempre que la fuerza externa neta sea cero, al igual que en la física clásica. Nuevamente vemos que la cantidad relativista se vuelve prácticamente la misma que la clásica a bajas velocidades. Es decir, el momento relativista\(\gamma mu\) se convierte\(mu\) en el clásico a bajas velocidades, porque\(\gamma\) es casi igual a 1 a velocidades bajas.
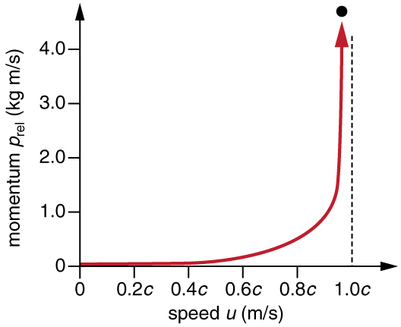
El impulso relativista tiene la misma sensación intuitiva que el impulso clásico. Es mayor para grandes masas que se mueven a altas velocidades, pero, debido al factor\(\gamma\), el impulso relativista se acerca al infinito a medida que\(u\) se acerca\(c\) (Figura\(\PageIndex{2}\)). Esta es otra indicación de que un objeto con masa no puede alcanzar la velocidad de la luz. Si lo hiciera, su impulso se volvería infinito, un valor irrazonable.
ALERTA DE CONCEPCIÓN errónea: Masa relativista e impulso
La definición relativisticamente correcta de impulso como\(p = \gamma mu\), a veces se toma para implicar que la masa varía con la velocidad:\(m_{var} = \gamma m\), particularmente en los libros de texto más antiguos. Sin embargo, tenga en cuenta que\(m\) es la masa del objeto medida por una persona en reposo en relación con el objeto. Así,\(m\) se define como la masa de reposo, la cual podría medirse en reposo, quizás usando la gravedad. Cuando una masa se mueve en relación con un observador, la única forma en que se puede determinar su masa es a través de colisiones u otros medios en los que esté involucrado el impulso. Dado que la masa de un objeto en movimiento no se puede determinar independientemente del momento, la única masa significativa es la masa de reposo. Así, cuando usamos el término masa, supongamos que es idéntico a la masa de reposo.
El impulso relativista se define de tal manera que la conservación del impulso se mantendrá en todos los marcos inerciales. Siempre que la fuerza externa neta sobre un sistema es cero, se conserva el impulso relativista, tal como es el caso del impulso clásico. Esto ha sido verificado en numerosos experimentos.
En la Sección de Energía Relativista, se explora la relación del impulso relativista con la energía. Ese sujeto producirá nuestro primer indicio de que los objetos sin masa también pueden tener ímpetu.
Ejercicio\(\PageIndex{1}\)
¿Cuál es el impulso de un electrón viajando a una velocidad\(0.985 c\)? La masa restante del electrón es\(9.11 \times 10^{-31} \, kg\).
- Responder
-
\[ \begin{align*} p &= \gamma mu \\[5pt] &= \dfrac{mu}{\sqrt{1 - \frac{u^2}{c^2}}} \\[5pt] &= \dfrac{(9.11 \times 10^{-31} kg) (0.985 c)(3.00 \times 10^8 m/s)}{\sqrt{1 - \frac{(0.985 c)2}{c^2}}} \\[5pt] &= 1.56 \times 10^{-21} kg \cdot m/s \end{align*} \]
Resumen
- La ley de conservación del impulso es válida siempre que la fuerza externa neta sea cero y para el impulso relativista. El impulso relativista\(p\) es el impulso clásico multiplicado por el factor relativista\(\gamma\)
- \(p = \gamma mu\), donde\(m\) está la masa de reposo del objeto,\(u\) es su velocidad relativa a un observador, y el factor relativista\(\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}.\)
- A bajas velocidades, el impulso relativista es equivalente al impulso clásico.
- El impulso relativista se acerca al infinito a medida que\(u\) se acerca\(c\). Esto implica que un objeto con masa no puede alcanzar la velocidad de la luz.
- Se conserva el impulso relativista, así como se conserva el impulso clásico.
Glosario
- impulso relativista
- \(p\), el momento de un objeto que se mueve a velocidad relativista;\(p = \gamma mu\), donde\(m\) está la masa de reposo del objeto,\(u\) es su velocidad relativa a un observador, y el factor relativista\(\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}\)
- masa de descanso
- la masa de un objeto medida por una persona en reposo en relación con el objeto


