1.5:1.5 Funciones trigonométricas

Última actualización
Guardar como PDF

Page ID: 126017

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Otro grupo de funciones extremadamente importante son las funciones trignonométricas fundamentales\(\sin\),\(\cos\), y\(\tan\). Estos se pueden definir en términos de las relaciones geométricas de los lados de los triángulos en ángulo recto, como se muestra a continuación:

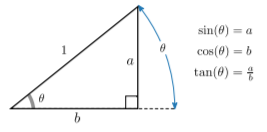
Si usamos esta definición básica, el dominio es\(\theta \in [0, \,\pi/2)\), donde el ángulo de entrada\(\theta\) se da en radianes.

Podemos generalizar la definición usando el siguiente esquema, que permite valores negativos de\(a\) y/o\(b\):

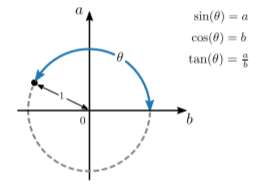
Con esto, el dominio se extiende a\(\theta \in [0,\,2\pi)\). Podemos extender aún más el dominio a todos los números reales,\(\theta \in \mathbb{R}\), tratando los valores de entrada módulo\(2\pi\) como equivalente; en otras palabras,\(f(\theta + 2\pi) = f(\theta)\). Con esta generalización, las funciones trigonométricas se convierten en funciones de muchos a uno.

Según el teorema de Pitágoras,\[\big[\sin(\theta)\big]^2 + \big[\cos(\theta)\big]^2 = 1.\] Usando esto, podemos pasar a probar una variedad de identidades, como las identidades de adición\[\begin{align} \sin(\theta_1 + \theta_2) &= \sin(\theta_1) \cos(\theta_2) + \cos(\theta_1)\sin(\theta_2) \\ \cos(\theta_1 + \theta_2) &= \cos(\theta_1) \cos(\theta_2) - \sin(\theta_1)\sin(\theta_2)\end{align}\] Como recordarás, las pruebas trigonométricas para estas identidades implican dibujar diagramas triangulares complicados, aplicando inteligentemente los pitagóricos fórmula, etc. Hay dos problemas con tales pruebas: (i) requieren algo de ingenio en la construcción de los diagramas triangulares, y (ii) puede no ser obvio si las pruebas funcionan si los ángulos se encuentran afuera\([0,\pi/2)\).

Felizmente, hay una solución a ambos problemas. Como veremos pronto, tales identidades trigonométricas se pueden probar algebraicamente mediante el uso de números complejos.