1.7: Continuidad

Última actualización
Guardar como PDF

Page ID: 126042

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Continuidad

La continuidad es un concepto importante en la teoría de las funciones reales. Una función continua es aquella cuya salida\(f(x)\) no sufre saltos bruscos cuando\(x\) cambia por pequeñas cantidades. Una función puede ser continua en todo su dominio, o solo en un subconjunto de su dominio. Por ejemplo,\(\sin(x)\) es continuo para todos\(x\), mientras que\(f(x) = 1/x\) es discontinuo en\(x = 0\). Otra función que es discontinua en\(x=0\) es la función de paso\[\Theta(x) = \left\{\begin{array}{ll} 1, &\;\;\;\textrm{for} \; x \ge 0\\ 0,&\;\;\; \textrm{otherwise.}\end{array}\right.\] Los matemáticos incluso han ideado funciones que son discontinuas en todas partes de su dominio, pero no vamos a estar lidiando con tales casos.

La definición rigurosa de continuidad es la siguiente:

Definición: Word

Una función\(f\) es continua en un punto\(x_0\) si, para alguno\(\epsilon >0\), podemos encontrar una\(\delta >0\) tal que establecer\(x\)\(x_0\) más cerca de que una distancia de\(\delta\)\(f(x)\)\(f(x_0)\) acerque a la distancia especificada\(\epsilon\).

Esa es una frase muy complicada, y puede ser más fácil de entender usando esta ilustración:

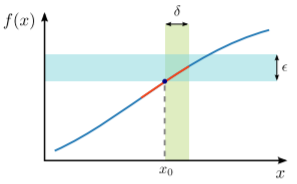
Un contraejemplo, con una función que tiene una discontinuidad en algunos\(x_0\), se muestra a continuación:

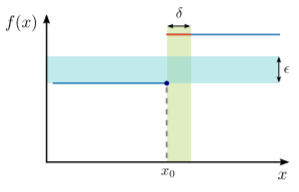
Si elegimos\(\epsilon\) menor que la brecha, entonces no importa qué valor\(\delta > 0\) intentemos, cualquier elección de\(0 < x < \delta\) dará un valor de\(f(x)\) eso está más\(\epsilon\) lejos que de\(f(x_0)\). De ahí que la condición de continuidad sea violada por elecciones suficientemente pequeñas de\(\epsilon = 1/2\), y decimos que\(f\) es discontinua en\(x_0\).