8.4: Cortes de Sucursales para Operaciones Generales Multi-Valoradas

Habiendo discutido las operaciones multivalorizadas más simples,\(z^p\) y\(\ln(z)\), aquí es cómo asignar cortes de sucursal para operaciones multivalorizadas más generales. Este es un proceso de dos pasos:

1. Localice los puntos de sucursal.

2. Asigne cortes de rama en el plano complejo, de tal manera que:
   • Cada punto de rama tiene un corte de rama que termina en él.

   • Cada corte de rama termina en un punto de rama.

   Tenga en cuenta que cualquier punto de rama que se encuentre en el infinito también debe obedecer estas reglas Los cortes de rama no deben cruzarse.

La elección de dónde colocar los cortes de rama no es única. Los cortes de rama generalmente se eligen para que sean líneas rectas, por simplicidad, pero esto no es necesario. Diferentes opciones de cortes de rama corresponden a diferentes formas de particionar los valores de la operación multivalorada en ramas separadas.

Un ejemplo importante

Podemos ilustrar el proceso de asignación de cortes de rama, y definir funciones de rama, utilizando la siguiente operación multivalorizada no trivial:\[f(z) = \ln\left(\frac{z+1}{z-1}\right).\] Esta es multivalorada debido a la presencia del logaritmo complejo. Los puntos de ramificación son\(z = 1\) y\(z = -1\), ya que estos son los puntos donde se convierte la entrada al logaritmo\(\infty\) o\(0\) respectivamente. Tenga en cuenta que *no*\(z = \infty\) es un punto de ramificación; at\(z = \infty\), la entrada al logaritmo es\(-1\), que no es un punto de ramificación para el logaritmo.

Podemos asignar cualquier corte de rama que se una a estos dos. A continuación se muestra una opción conveniente:

Figura\(\PageIndex{1}\)

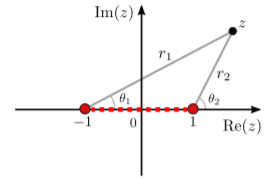
Esta elección de corte de rama es agradable porque podemos expresar los\(z - 1\) términos\(z+1\) y usando las representaciones polares\[\begin{align} z + 1 &= r_1\,e^{i\theta_1}, \\ z - 1 &= r_2\, e^{i\theta_2},\end{align}\] donde\(r_1\),\(r_2\),\(\theta_1\), y se\(\theta_2\) muestran gráficamente en lo anterior figura. El posicionamiento del corte de rama corresponde a una elección particular para los rangos de los argumentos complejos\(\theta_1\) y\(\theta_2\). Como veremos en breve, la elección actual del corte de rama corresponde a\[\theta_1 \in (-\pi,\pi), \quad \theta_2 \in (-\pi,\pi).\] Por lo tanto, en términos de esta representación polar, se\(f(z)\) puede escribir como\[\begin{align} \begin{aligned} f(z) = \ln\left(\frac{r_1}{r_2}\right) + i(\theta_1 - \theta_2 + 2\pi m), \quad m\in\mathbb{Z}, \\ \mathrm{where}\; z = -1 + r_1\,e^{i\theta_1} = 1 + r_2\,e^{i\theta_2},\quad\theta_1, \theta_2 \in (-\pi,\pi). \end{aligned}\end{align}\] La elección de\(m\) especifica la rama, y podemos elegir\(m = 0\) como principal rama.

Ahora verifiquemos ese ajuste\(\theta_1 \in (-\pi,\pi)\) y\(\theta_2 \in (-\pi,\pi)\) sea consistente con nuestra elección de corte de rama. Considera la rama principal, y compara los resultados de la fórmula anterior para\(z\) justo por encima del eje real, y por\(z\) justo debajo del eje real. Hay tres casos de interés. En primer lugar, para\(\mathrm{Re}(z) < 1\) (a la izquierda del punto de ramificación más a la izquierda),\[\begin{align} \mathrm{Im}(z) &= 0^+ \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((\pi) - (\pi)\Big) \quad = \ln\left(\frac{r_1}{r_2}\right) \\ \mathrm{Im}(z) &= 0^- \;\;\Rightarrow \;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((-\pi) - (-\pi)\Big) = \ln\left(\frac{r_1}{r_2}\right).\end{align}\] Así, no hay discontinuidad a lo largo de este segmento del eje real.

En segundo lugar, para\(-1 < \mathrm{Re}(z) < 1\) (entre los dos puntos de ramificación),\[\begin{align} \mathrm{Im}(z) &= 0^+ \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (\pi)\Big) \;\;= \ln\left(\frac{r_1}{r_2}\right) -i\pi \\ \mathrm{Im}(z) &= 0^- \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (-\pi)\Big) = \ln\left(\frac{r_1}{r_2}\right) + i\pi.\end{align}\] De ahí que en el segmento entre los dos puntos de ramificación, hay una discontinuidad de\(\pm 2\pi i\) en diferentes lados del eje real. El valor de esta discontinuidad es exactamente igual, por supuesto, a la separación entre las diferentes ramas del logaritmo complejo.

Por último, para\(\mathrm{Re}(z) > 1\) (a la derecha del punto de bifurcación más a la derecha), nuevamente no hay discontinuidad:\[\begin{align} \mathrm{Im}(z) &= 0^+ \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (0)\Big) = \ln\left(\frac{r_1}{r_2}\right) \\ \mathrm{Im}(z) &= 0^- \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (0)\Big) = \ln\left(\frac{r_1}{r_2}\right).\end{align}\]