9.3: Postes

En el apartado anterior, nos referimos a situaciones en las\(f(z)\) que no es analítico en puntos discretos. “Discreto”, en este contexto, significa que cada punto de no analitticidad está rodeado por una región finita sobre la cual\(f(z)\) es analítica, aislándola de otros puntos de no analitticidad. Tales situaciones suelen surgir de funciones de la forma\[f(z) \approx \frac{A}{(z-z_0)^n}, \quad \mathrm{where}\;\; n\in\{1,2,3,\dots\}.\] For\(z = z_0\), la función es no analítica porque su valor es singular. Se dice que tal función tiene un polo en\(z_0\). El entero\(n\) se llama el orden del polo.

Residuo de un poste simple

Los polos de orden 1 se llaman polos simples, y son de especial interés. Cerca de un polo simple, la función tiene la forma\[f(z) \approx \frac{A}{z-z_0}.\] En este caso, el numerador complejo\(A\) se llama el residuo del polo (así llamado porque es lo que queda si le quitamos el factor singular correspondiente al polo). El residuo de una función en un punto\(z_0\) se denota comúnmente\(\mathrm{Res}[f(z_0)]\). Tenga en cuenta que si una función es analítica en\(z_0\), entonces\(\mathrm{Res}[f(z_0)] = 0\).

Ejemplo\(\PageIndex{1}\)

Considera la función\[f(z) = \frac{5}{i-3z}.\] Para encontrar el polo y el residuo, divide el numerador y el denominador por\(-3\):\[f(z) = \frac{-5/3}{z-i/3}.\] Así, hay un polo simple en\(z = i/3\) con residuo\(-5/3\).

Ejemplo\(\PageIndex{2}\)

Considera la función\[f(z) = \frac{z}{z^2 + 1}.\] Para encontrar los polos y residuos, factorizamos el denominador:\[f(z) = \frac{z}{(z+i)(z-i)}.\] De ahí, hay dos polos simples, at\(z = \pm i\).

Para encontrar el residuo en\(z = i\), separamos la parte divergente para obtener\[\begin{align} f(z) &= \frac{\left(\frac{z}{z+i}\right)}{z-i} \\ \Rightarrow\quad \mathrm{Res}\big[\,f(z)\,\big]_{z=i} &= \left[\frac{z}{z+i}\right]_{z=i} = 1/2. \end{align}\] De igual manera, para el otro polo,\[\mathrm{Res}\big[\,f(z)\,\big]_{z=-i} = \left[\frac{z}{z-i}\right]_{z=-i} = 1/2.\]

El teorema del residuo

En la Sección 9.1, se utilizó la parametrización del contorno para calcular\[\oint_{\Gamma} \frac{dz}{z} = 2\pi i,\] dónde\(\Gamma\) se encuentra un bucle circular en sentido contrario a las agujas del reloj centrado en el origen. Esto se mantiene para cualquier radio de bucle (distinto de cero). Combinando esto con los resultados de la Sección 9.2, podemos obtener el teorema del residuo:

Teorema\(\PageIndex{1}\)

Para cualquier función analítica\(f(z)\) con un polo simple en\(z_0\),\[\oint_{\Gamma[z_0]} dz \; f(z) = \pm 2\pi i \, \mathrm{Res}\big[\,f(z)\,\big]_{z = z_0},\] donde\(\Gamma[z_0]\) denota un bucle infinitesimal alrededor\(z_0\). El\(+\) letrero se mantiene para un bucle en sentido antihorario, y el\(-\) signo para un bucle en sentido horario.

Al combinar el teorema del residuo con los resultados de las últimas secciones, llegamos a una técnica para integrar una función\(f(z)\) sobre un bucle\(\Gamma\), llamada cálculo de residuos:

1. Identificar los polos de\(f(z)\) en el dominio encerrado por\(\Gamma\).

2. Verifique que todos estos sean polos simples, y que no\(f(z)\) tengan otros comportamientos no analíticos (por ejemplo, cortes de ramificación) en la región cerrada.

3. Calcular el residuo,\(\mathrm{Res}[f(z_n)]\), en cada polo\(z_n\).

4. El valor de la integral de bucle es\[\oint_\Gamma dz\; f(z) = \pm 2\pi i \sum_n \mathrm{Res}\big[\,f(z)\,\big]_{z = z_n}.\] El signo más se mantiene si\(\Gamma\) es en sentido contrario a las agujas del reloj, y el signo menos si es en sentido horario.

Ejemplo del cálculo de residuos

Considera\[f(z) = \frac{1}{z^2 + 1}.\] Esto se puede reescribir como\[f(z) = \frac{1}{(z + i)\,(z-i)}.\] Por inspección, podemos identificar dos polos: uno en\(+i\), con residuo\(1/2i\), y el otro en\(-i\), con residuo\(-1/2i\). La función es analítica en todas partes.

Supongamos que nos integramos\(f(z)\) alrededor de un contorno en sentido antihorario\(\Gamma_1\) que encierra solo el polo en\(+i\), como lo indica la curva azul en la siguiente figura:

Figura\(\PageIndex{1}\)

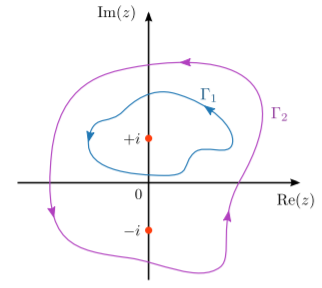
De acuerdo con el teorema del residuo, el resultado es\[\begin{align} \oint_{\Gamma_1}dz \; f(z) &= 2\pi i\, \mathrm{Res}\big[\,f(z)\,\big]_{z = i} \\ &= 2\pi i \cdot \frac{1}{2i} \\& = \pi.\end{align}\] Por otro lado, supongamos que integramos alrededor de un contorno\(\Gamma_2\) que encierra ambos polos, como lo muestra la curva púrpura. Entonces el resultado es\[\oint_{\Gamma_2}dz \; f(z) = 2\pi i \cdot \left[\frac{1}{2i} - \frac{1}{2i}\right] = 0.\]