9.4: Uso de la integración de Contour para resolver integrales definidas

El cálculo de residuos nos permite emplear la integración de contornos para resolver integrales definidas sobre el dominio real. El truco es convertir la integral definida en una integral de contorno, y luego resolver la integral de contorno usando el teorema de residuo.

A modo de ejemplo, consideremos la integral definida\[\int_{-\infty}^\infty \frac{dx}{x^2 + 1}.\] Esta integral se toma sobre valores reales de\(x\), y en el Capítulo 3 la resolvimos usando un cambio de variables. Ahora veamos cómo resolverlo usando la integración de contorno.

Primero, generalizar el integrando de una función de\(x\) a una función analítica de\(z\). (Este procedimiento se llama continuación analítica). Por lo general, elegimos el nuevo integrando (complejo) para que se reduzca al viejo integrando para\(z \in \mathbb{R}\), y sea analítico sobre un dominio amplio. En este caso, vamos\[\frac{1}{x^2 + 1} \rightarrow \frac{1}{z^2 + 1}.\] Este es solo el integrando que tratamos en la Sección 9.3.

Ahora tenemos que elegir el contorno. El procedimiento habitual es definir un contorno cerrado (bucle), de tal manera que un segmento del bucle sea la línea real (de\(-\infty\) a\(+\infty\)), y el otro segmento del bucle “dobla hacia atrás” en el plano complejo para cerrar el bucle. Esto se llama cerrar el contorno.

Aquí, elegimos cerrar el contorno a lo largo de un arco semicircular antihorario en la mitad superior del plano complejo, como se muestra a continuación:

Figura\(\PageIndex{1}\)

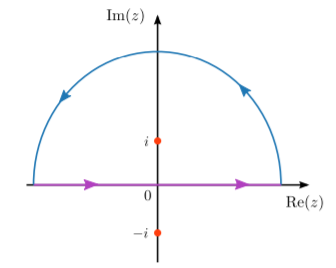
El contorno de bucle resultante encierra el polo en\(z = +i\), por lo que\[\oint \frac{dz}{z^2+1} = 2\pi i \; \mathrm{Res}\left[\frac{1}{z^2 + 1}\right]_{z = +i} = \pi.\] Tenga en cuenta que el bucle está en sentido antihorario, por lo que tomamos el signo positivo para el teorema del residuo. La integral de bucle también se puede escribir como una suma de dos integrales:\[\oint \frac{dz}{z^2 + 1} = \int_{-\infty}^\infty \frac{dx}{x^2 + 1} \;+\; \int_{\mathrm{arc}} \frac{dz}{z^2 + 1}.\] El primer término es la integral que nos interesa. El segundo término, la integral de contorno a lo largo del arco, va a cero. Para ver por qué, observar que a lo largo de un arco de radio\(R\), la magnitud del integrando va como\(1/R^{2}\), mientras que la\(dz\) da otro factor de\(R\) (ver Sección 9.1), por lo que la integral global va como\(1/R\), que desaparece como\(R \rightarrow \infty\).

Obtenemos así el resultado\[\int_{-\infty}^\infty \frac{dx}{x^2 + 1} = \pi.\] Como ejercicio, se puede verificar que cerrar el contorno en el medio plano inferior conduce exactamente al mismo resultado.

El lema de Jordan

Antes de proceder a usos más complicados de la integración de contornos, debemos discutir un resultado importante llamado lema de Jordan:

Teorema\(\PageIndex{1}\)

Dejar\[I = \int_C dz \; e^{iqz} \,g(z),\] donde\(q\) es cualquier constante real positiva, y el contorno\(C\) que es un arco semicircular de radio\(R\) en el medio plano superior, centrado en el origen. Entonces\[\text{If}\;\; \big|\,g(z)\,\big| < g_{\mathrm{max}} \;\;\;\text{for all}\;\;z \in C \;\;\;\Rightarrow \;\;\; I \rightarrow 0 \;\;\mathrm{as}\;\; g_{\mathrm{max}} \rightarrow 0.\]

En otras palabras, si el factor de\(g(z)\) en el integrando no explota a lo largo del contorno del arco (es decir, su valor está acotado), entonces en el límite donde el valor delimitador va a cero, el valor de toda la integral desaparece.

Por lo general, el caso limitante de interés es cuando el radio del arco va al infinito. Aunque el integrando se desvanezca en ese límite, puede que no sea obvio que la integral se\(I\) desvanece, porque la integración se toma a lo largo de un arco de longitud infinita (entonces tenemos una\(0\times\infty\) especie de situación). El lema de Jordan resulta entonces útil, ya que proporciona un conjunto de criterios que pueden permitirnos concluir instantáneamente que\(I\) debería desaparecer.

La prueba del lema de Jordan es tediosa, y no entraremos en sus detalles.

Para los integrandos que contienen un prefactor de\(e^{-iqz}\) más que\(e^{iqz}\) (de nuevo, dónde\(q \in \mathbb{R}^+\)), se sostiene una versión diferente del lema de Jordan, refiriéndose a un contorno\(C'\) en el medio plano inferior:

Teorema\(\PageIndex{2}\)

Dejar\[I = \int_C dz \; e^{-iqz} \,g(z),\] donde\(q\) es cualquier constante real positiva, y el contorno\(C\) que es un arco semicircular de radio\(R\) en el medio plano inferior, centrado en el origen. Entonces\[\text{If}\;\; \big|\,g(z)\,\big| < g_{\mathrm{max}} \;\;\;\text{for all}\;\;z \in C \;\;\;\Rightarrow \;\;\; I \rightarrow 0 \;\;\mathrm{as}\;\; g_{\mathrm{max}} \rightarrow 0.\]

Esto se ve fácilmente haciendo el cambio de variable\(z \rightarrow -z\) sobre la forma original del lema de Jordan.

Como una forma conveniente de recordar qué variante del lema de Jordania usar, piense en qué extremo del eje imaginario hace que el factor exponencial desaparezcan:\[\begin{aligned} e^{iqz}\big|_{z = i\infty}\;\; = e^{-\infty} = 0\quad & \Rightarrow \;\; e^{iqz} \;\;\;\,\text{vanishes far above the origin}. \\ e^{-iqz}\big|_{z = -i\infty} = e^{-\infty} = 0\quad & \Rightarrow \;\; e^{-iqz} \;\;\textrm{vanishes far below the origin}.\end{aligned}\] De ahí que para\(e^{iqz}\) (dónde\(q\) está cualquier número real positivo), la supresión ocurre en el medio plano superior. Porque\(e^{-iqz}\), la supresión ocurre en el medio plano inferior.

Una integral de contorno usando el lema de Jordan

Considera la integral\[I = \int_{-\infty}^\infty dx\; \frac{\cos(x)}{4x^2 + 1}.\] Un enfoque posible es romper el coseno en\((e^{ix} + e^{-ix})/2\), y hacer el contorno integral en cada pieza por separado. Otro enfoque, que ahorra un poco de esfuerzo, es escribir\[I = \mathrm{Re} \; \int_{-\infty}^\infty dx\; \frac{e^{ix}}{4x^2 + 1}.\] Para hacer la integral, cerrar el contorno en el medio plano superior:

Figura\(\PageIndex{2}\)

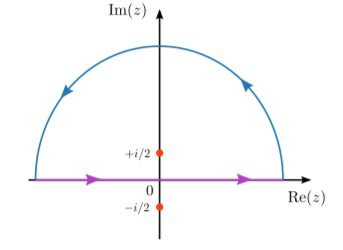
Entonces del\[\oint dz \; \frac{e^{iz}}{4z^2 + 1} = \int_{-\infty}^\infty dx\; \frac{e^{ix}}{4x^2 + 1} + \int_{\mathrm{arc}} dz \; \frac{e^{iz}}{4z^2 + 1}.\] lado derecho, el primer término es lo que queremos. El segundo término es un arco en sentido antihorario en el medio plano superior. Según el lema de Jordan, este término va a cero ya que el radio del arco va al infinito, ya que el resto del integrando va a cero para grandes\(|z|\): En\[\left|\frac{1}{4z^2 + 1}\right| \sim \frac{1}{4|z|^2} \rightarrow 0 \quad \mathrm{as} \;|z| \rightarrow \infty.\] cuanto al contorno del bucle, se puede evaluar utilizando el teorema del residuo:\[\begin{align} \oint dz \; \frac{e^{iz}}{4z^2 + 1} &= \mathrm{Res}\left[\frac{e^{iz}}{4z^2 + 1}\right]_{\mathrm{enclosed}\;\mathrm{poles}}\\ &= 2\pi i \; \mathrm{Res}\left[\frac{1}{4}\, \frac{e^{iz}}{(z+i/2)(z-i/2)}\right]_{z = i/2} \\ &= 2\pi i \; \frac{e^{-1/2}}{4i}.\end{align}\] De ahí,\[I = \mathrm{Re}\;\left[\frac{\pi}{2\sqrt{e}}\right]= \frac{\pi}{2\sqrt{e}}.\] Al resolver la integral esto manera, debemos cerrar el contorno en el medio plano superior porque nuestra elección de integrando complejo estaba delimitada en el medio plano superior. Alternativamente, podríamos haber optado por escribir\[I = \mathrm{Re} \; \int_{-\infty}^\infty dx\; \frac{e^{-ix}}{4x^2 + 1},\] es decir, con\(e^{ix}\) en\(e^{-ix}\) lugar de en el numerador. En ese caso, el lema de Jordan nos dice cerrar el contorno en el medio plano inferior. El arco en el medio plano inferior se desvanece, como antes, mientras que el contorno del bucle está en el sentido de las agujas del reloj (aportando un signo menos extra) y encierra el polo inferior:\[\begin{align} \oint dz \frac{e^{-iz}}{4z^2 + 1} &= -2\pi i \, \mathrm{Res}\left[ \frac{e^{-iz}}{4z^2 + 1} \right]_{z = -i/2} \\ &= - 2\pi i \frac{e^{-1/2}}{-4i} \\ &= \frac{\pi}{2\sqrt{e}}.\end{align}\] Tomando la parte real, obtenemos el mismo resultado que antes.

Integrales de valor principal

A veces, nos encontramos con integrales que tienen polos tendidos en el contorno de integración deseado.

Como ejemplo, considere\[I = \int_{-\infty}^\infty dx\; \frac{\sin(x)}{x}.\] Debido a la expansión en serie de la función sinusoidal, el integrando no diverge en\(x = 0\), y la integral es de hecho convergente. La integral puede resolverse sin usar números complejos usando el truco arcano de diferenciar bajo el signo integral (ver Sección 3.6). Pero también se puede resolver directamente a través de la integración de contornos, con solo unos pocos pasos adicionales.

Empezamos por escribir\[I = \mathrm{Im}(I'), \quad \mathrm{where}\;\;\; I' = \int_{-\infty}^\infty dx\; \frac{e^{ix}}{x}.\] Queremos calcular\(I'\) con la ayuda de la integración de contornos. Pero hay algo extraño en\(I'\): el complejo integrando tiene un polo en\(z = 0\), ¡justo en la línea real!

Para manejar esto, nos\(I'\) dividimos en dos integrales, una repasando\(-\infty < x < -\epsilon\) (donde\(\epsilon\) hay algunos infinitesimales positivos), y la otra sobre\(\epsilon < x < \infty\):\[\begin{align} I' &= \lim_{\epsilon \rightarrow 0} \left[ \int_{-\infty}^{-\epsilon} dx\; \frac{e^{ix}}{x} + \int_{\epsilon}^\infty dx\; \frac{e^{ix}}{x}\right] \\ &\equiv \mathcal{P} \int_{-\infty}^\infty dx\; \frac{e^{ix}}{x}.\end{align}\] En la última línea, la notación\(\mathcal{P}[\cdots]\) es de mano corta para esto procedimiento de “cortar” un segmento infinitesimal que rodea el polo. A esto se le llama tomar el valor principal de la integral.

Nota

A pesar de que esto lleva el mismo nombre que los “valores principales” para las operaciones complejas multivalorizadas discutidas en el Capítulo 8, no hay conexión entre ambos conceptos.

Ahora considere el contorno de bucle que se muestra en la siguiente figura. El bucle sigue el contorno del valor principal a lo largo del eje real, salta sobre el polo en\(z = 0\) y se curva hacia atrás a lo largo del semiplano superior. Como no encierra polos, la integral de bucle desaparece por el teorema integral de Cauchy. Sin embargo, el bucle también se puede descomponer en varios subcontornos:

1. \(\Gamma_1\), que consiste en los segmentos a lo largo del eje real.

2. \(\Gamma_2\), el gran arco semicircular en sentido antihorario.

3. \(\Gamma_3\), el arco semicircular infinitesimal en el sentido de las agujas del reloj que salta alrededor\(z = 0\).

Figura\(\PageIndex{3}\)

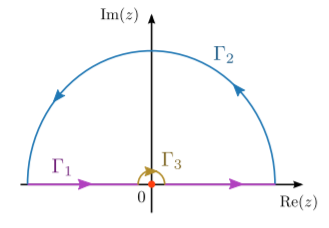
La integral sobre\(\Gamma_1\) es la integral principal-valor que nos interesa. El sobre integral se\(\Gamma_2\) desvanece por el lema de Jordan. La integral sobre se\(\Gamma_3\) puede calcular por parametrización:\[\begin{align} \int_{\Gamma_3} \frac{e^{iz}}{z} &= \lim_{\epsilon \rightarrow 0} \int_{\pi}^{0} \frac{e^{i\epsilon \exp(i\theta)}}{\epsilon e^{i\theta}} \left(i\epsilon e^{i\theta}\right) d\theta \\ &= \lim_{\epsilon \rightarrow 0} i \int_{\pi}^0 d\theta \\ &= - i\pi.\end{align}\] Intutivamente, ya que rodear un polo en sentido antihorario da un factor de\(2\pi i\) veces el residuo (que es 1 en este caso), un semicírculo en el sentido de las agujas del reloj se asocia con un factor de\(- i \pi\). Por último, poniendo todo junto,\[\underbrace{\int_{\Gamma_1 + \Gamma_2 + \Gamma_3} f(z) dz}_{ =~0~(\text{Cauchy's integral theorem})} = \underbrace{\int_{\Gamma_1} f(z) dz}_{=~I'} + \underbrace{\int_{\Gamma_2} f(z) dz}_{=~0~(\text{Jordan's lemma})} + \underbrace{\int_{\Gamma_3} f(z) dz.}_{=~-i \pi}\] De ahí,\[I = \mathrm{Im}(I') = \mathrm{Im}(i\pi) = \pi.\] Esto concuerda con el resultado obtenido por el método de diferenciar bajo el signo integral de la Sección 3.6.

Alternativamente, podríamos haber elegido el contorno de bucle para que salte por debajo del poste en\(z = 0\). En ese caso, la integral de bucle sería distinta de cero, y puede evaluarse usando el teorema del residuo. El resultado final es el mismo.