9.5: Ejercicios

Ejercicio\(\PageIndex{1}\)

¿Está bien definido el concepto de integral de contorno si el integrando no\(f(z)\) es diferenciable a lo largo del contorno? ¿Por qué o por qué no?

Ejercicio\(\PageIndex{2}\)

En la Sección 9.4, nos ocupamos de la integral\[\int_{-\infty}^\infty \frac{dx}{x^2 + 1}.\] Rehacer este cálculo, pero esta vez cerramos el contorno en el medio plano inferior. Demostrar que el resultado es el mismo.

Contestar

Por continuación analítica, considere la integral\[I = \oint \frac{dz}{z^4 + 1},\] donde se cierra el contorno en el medio plano superior (también podríamos optar por cerrar por debajo sin cambiar los resultados). El contorno integral sobre el arco grande escala con el radio del arco\(R\) como\(R^{-3}\), por lo que se desvanece como\(R \rightarrow \infty\). De ahí\(I\) que sea exactamente igual a la integral definitiva que buscamos.

Para evaluar la integral de bucle, necesitamos los polos del integrando, que son las soluciones a\(z^4 = -1\). Escribiendo\(-1 = \exp(i\pi)\), encontramos que las raíces son\(\exp(i\pi/4) \times \{\text{4-roots of unity}\}.\) Estas se pueden escribir en la representación cartesiana como\[\begin{align} z_1 &= \frac{1+i}{\sqrt{2}} \\ z_2 &= \frac{-1+i}{\sqrt{2}} \\ z_3 &= \frac{-1-i}{\sqrt{2}} \\ z_4 &= \frac{1-i}{\sqrt{2}}.\end{align}\] Al cerrar el contorno arriba, adjuntamos\(z_1\) y\(z_2\). Así, por el teorema del residuo,\[\begin{align} I &= 2\pi i \left\{\left[\mathrm{Res} \left(\frac{1}{z^4 + 1}\right)\right]_{z=z_1} + \left[\mathrm{Res} \left(\frac{1}{z^4 + 1}\right)\right]_{z=z_2}\right\} \\ &= 2\pi i\left[\frac{1}{(z_1-z_2)(z_1-z_3)(z_1-z_4)} + \frac{1}{(z_2-z_1)(z_2-z_3)(z_2-z_4)}\right] \\ &= 2\pi i \left[\frac{\sqrt{8}}{(2)(2+2i)(2i)} + \frac{\sqrt{8}}{(-2)(2i)(-2+2i)}\right] \\ &= \frac{\sqrt{2}\pi i}{2} \left[\frac{1}{-1+i} + \frac{1}{1+i}\right] \\ &= \frac{\pi}{\sqrt{2}}.\end{align}\]

Ejercicio\(\PageIndex{3}\)

Calcular\[\int_{-\infty}^\infty dx\; \frac{1}{x^4 + 1}.\]

Ejercicio\(\PageIndex{4}\)

Calcular\[\int_{-\infty}^\infty dx\; \left[\frac{\sin(x)}{x}\right]^2.\]

Ejercicio\(\PageIndex{5}\)

Calcular\[\int_0^\infty dx \frac{x^{\lambda}}{x+1}, \;\;\mathrm{where}\; -1 < \lambda < 0.\] pista: coloque el corte de rama del integrando a lo largo del eje real positivo.

Ejercicio\(\PageIndex{6}\)

Resolver la integral definida\[I = \int_0^{2\pi} \frac{d\phi}{\cos\phi+3},\] a través de los siguientes pasos. Primero, mostrar que a lo largo de un círculo unitario en el plano complejo centrado en el origen,\[\cos\phi = \frac{1}{2}\left(z+\frac{1}{z}\right),\] donde\(z(\phi) = \exp(i\phi)\). Después definir una función compleja\(f(z)\) tal que la integral de bucle\(\oint f(z) \;dz,\) tomada sobre el contorno circular, sea igual a\(I\). De ahí, calcular\(I\).

Contestar

Un círculo unitario centrado en el origen puede ser parametrizado por\(z = \exp(i\phi)\). De ahí que, a lo largo de este círculo,\[\begin{align} \cos\phi &= \frac{1}{2}\left(e^{i\phi} + e^{-i\phi}\right) \\ &= \frac{1}{2} \left(e^{i\phi} + \frac{1}{e^{i\phi}}\right) \\ &= \frac{1}{2}\left(z + \frac{1}{z}\right).\end{align}\] También,\[\frac{dz}{d\phi} = iz.\] denotemos este contorno circular por\(\Gamma\). Queremos encontrar una función\(f(z)\) tal que\[\oint_\Gamma f(z) \;dz = \int_0^{2\pi} \frac{d\phi}{\cos\phi+3}.\] La integral de contorno en el lado izquierdo se pueda parametrizar como\[\int_0^{2\pi} d\phi\; f\big(z(\phi)\big)\, \frac{dz}{d\phi}.\] Por lo tanto, queremos\(f(z)\) tal que\[\begin{align} f\big(z(\phi)\big) \frac{dz}{d\phi} &= \frac{1}{\cos\phi+3} \\ = f(z) \;\,(i z) &= \frac{1}{\frac{1}{2}\left(z+\frac{1}{z}\right) + 3}.\end{align}\] Después de un poco de álgebra, obtengamos\[f(z) = \frac{-2i}{z^2 + 6z + 1}.\] El denominador en\(f(z)\) tiene dos raíces, que son ambas reales:\[\begin{align} z_+ &= -3 + 2\sqrt{2} = - 0.17157\dots \\ z_- &= -3 - 2\sqrt{2} = -5.8284\dots\end{align}\] Solo el\(z_+\) poste está encerrado por el círculo unitario. Así, podemos utilizar el teorema del residuo para evaluar la integral:\[\begin{align} I = \oint_\Gamma \frac{-2i}{z^2 + 6z + 1} \, dz &= 2\pi i \; \mathrm{Res}\left[\frac{-2i}{(z-z_+)(z-z_-)}\right]_{z = z_+} \\ &= 2\pi i \left(\frac{-2i}{z_+-z_-}\right) \\ &= \frac{4\pi}{\left(-3 + 2\sqrt{2}\right)-\left(-3 - 2\sqrt{2}\right)} \\ &= \frac{\pi}{\sqrt{2}}.\end{align}\]

Ejercicio\(\PageIndex{7}\)

Supongamos que\(f(z)\) es analítico en todas partes en el medio plano superior, incluida la línea real, y que su magnitud se desvanece tan\(1/|z|\) o más rápido como\(|z| \rightarrow \infty\). Encuentra el valor de la integral principal-valor\[\mathcal{P}\left[\int_{-\infty}^\infty \frac{f(x)}{x-a} dx \right],\] donde\(a\) hay alguna constante real. De ahí, demostrar que las partes reales e imaginarias de\(f\) lo largo de la línea real están relacionadas por\[\begin{align} \mathrm{Re}\big[f(x)\big] &= \;\;\,\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Im}[f(w)]}{w-x} dw\right] \\ \mathrm{Im}\big[f(x)\big] &= -\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Re}[f(w)]}{w-x} dw\right]. \end{align}\] Estas se llaman las relaciones Kramers-Kronig. En física, estas relaciones imponen importantes restricciones a la dependencia de frecuencia de las partes real e imaginaria de la función dieléctrica (el cuadrado del índice de refracción complejo).

Contestar

Para evaluar la integral de valor principal\[I = \mathcal{P}\left[\int_{-\infty}^\infty \frac{f(x)}{x-a} dx \right],\] se introduce el siguiente contorno de bucle:

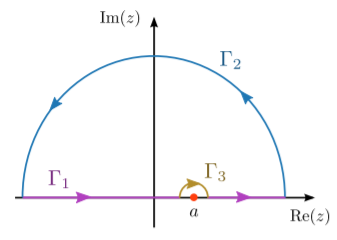
Figura\(\PageIndex{1}\)

El procedimiento de solución es muy similar al ejemplo elaborado en la Sección 9.4. A partir de las propiedades de\(f(z)\) dado en la declaración del problema, podemos concluir que (i) el integrando es analítico sobre y dentro del contorno del bucle, por lo que se puede utilizar el teorema del residuo; y (ii) el integrando desaparece lo suficientemente rápido lejos del origen para que, por el lema de Jordania, la integral sobre\(\Gamma_2\) se desvanece. De ahí,\[I = i \pi f(a).\] al volver a marcar las variables ficticias\(x \rightarrow y\) y\(a \rightarrow x\), podemos escribir\[f(x) = -\frac{i}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{f(y)}{y-x} dy \right].\] Vamos a romper ahora\(f\) en sus partes real e imaginaria:\[\begin{align} \mathrm{Re}[f(x)] + i \mathrm{Im}[f(x)] &= -\frac{i}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Re}[f(y)] + i \mathrm{Im}[f(y)]}{y-x} \;dy \right] \\ &= \frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Im}[f(y)] -i\mathrm{Re}[f(y)]}{y-x} \;dy \right].\end{align}\] Equiparando las partes real e imaginaria de los dos lados, obtenemos las siguientes dos ecuaciones reales, que son los Kramers- Relaciones Kronig:\[\begin{align} \mathrm{Re}[f(x)] &= \;\;\,\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Im}[f(y)]}{y-x} \;dy \right] \\ \mathrm{Im}[f(x)] &= -\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Re}[f(y)]}{y-x} \; dy \right].\end{align}\]