10.1: Serie de Fourier
- Page ID
- 125961
Comenzamos discutiendo la serie de Fourier, la cual es utilizada para analizar funciones que son periódicas en sus entradas. Una función periódica\(f(x)\) es una función de una variable real\(x\) que se repite cada vez que\(x\) cambia por\(a\), como se muestra en la siguiente figura:
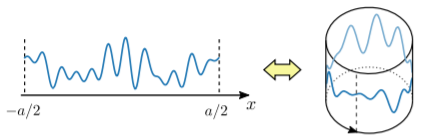
A la constante\(a\) se le llama el periodo. Matemáticamente, escribimos la condición de periodicidad como\[f(x+a) = f(x), \quad\forall\;\, x\in \mathbb{R}.\] El valor de\(f(x)\) puede ser real o complejo, pero\(x\) debe ser real. Se puede pensar en\(x\) representar una coordenada espacial. (La siguiente discusión también se aplica a las funciones del tiempo, aunque con diferencias menores en la convención que se discuten en la Sección 10.3.) También podemos pensar en la función periódica como definida sobre un segmento finito\(-a/2 \le x < a/2\), con condiciones de límite periódicas\(f(-a/2) = f(a/2)\). En términos espaciales, esto es como envolver el segmento en un bucle:
Consideremos lo que significa especificar una función periódica\(f(x)\). Una forma de especificar la función es darle una fórmula matemática explícita para ello. Otro enfoque podría ser especificar los valores de función en\(-a/2 \le x < a/2\). Dado que hay un número infinitamente infinito de puntos en este dominio, generalmente solo podemos lograr una especificación aproximada de\(f\) esta manera, dando los valores de\(f\)\(x\) puntos de ajuste grandes pero finitos.
Hay otro enfoque interesante para especificar\(f\). Podemos expresarlo como una combinación lineal de funciones periódicas más simples, que consiste en senos y cosenos: A\[f(x) = \sum_{n=1}^\infty \alpha_n \sin\left(\frac{2\pi n x}{a}\right) + \sum_{m=0}^\infty \beta_m \cos\left(\frac{2 \pi m x}{a}\right).\] esto se le llama serie de Fourier. Dado el conjunto de números\(\{\alpha_n, \beta_m\}\), que se denominan los coeficientes de Fourier, se\(f(x)\) pueden calcular para cualquiera\(x\). Tenga en cuenta que los coeficientes de Fourier son reales si\(f(x)\) es una función real, o complejos si\(f(x)\) es complejo.
La justificación de la fórmula de la serie de Fourier es que las funciones seno y coseno en la serie son, en sí mismas, periódicas con período\(a\):\[\begin{align} \sin\left(\frac{2\pi n (x+a)}{a}\right) = \sin\left(\frac{2\pi n x}{a} + 2\pi n\right) &= \sin\left(\frac{2\pi n x}{a}\right) \\ \cos\left(\frac{2\pi m (x+a)}{a}\right) = \cos\left(\frac{2\pi m x}{a} + 2\pi m\right) &= \cos\left(\frac{2\pi m x}{a}\right).\end{align}\] De ahí que cualquier combinación lineal de ellas satisface automáticamente la condición de periodicidad para\(f\). (Tenga en cuenta que en la fórmula de la serie de Fourier, el\(n\) índice no incluye 0. Dado que el término seno con se\(n = 0\) desvanece para todos\(x\), es redundante.)
Funciones integrables al cuadrado
La serie de Fourier es un concepto agradable, pero ¿las funciones periódicas arbitrarias pueden expresarse siempre como una serie de Fourier? Esta pregunta resulta sorprendentemente intrincada, y su resolución preocupó a los matemáticos durante gran parte del siglo XIX. La discusión completa está más allá del alcance de este curso.
Por suerte, resulta que una cierta clase de funciones periódicas, que se encuentran comúnmente en contextos físicos, están garantizadas para ser siempre expresables como series de Fourier. Se trata de funciones integrables al cuadrado, para las cuales\[\int_{-a/2}^{a/2} dx\; \big|\,f(x)\,\big|^2\;\;\text{exists and is finite}.\] A menos que se indique lo contrario, siempre asumiremos que las funciones con las que estamos tratando son integrables al cuadrado.
Serie compleja de Fourier y relaciones inversas
Usando la fórmula de Euler, podemos reescribir la serie de Fourier de la siguiente manera:\[f(x) = \sum_{n=-\infty}^\infty e^{2\pi i n x/a}\, f_n.\] En lugar de sumas separadas sobre senos y cosenos, tenemos una sola suma sobre exponenciales complejos, que es más ordenada. La suma incluye enteros negativos\(n\), e involucra un nuevo conjunto de coeficientes de Fourier\(f_n\), que son números complejos. (Como ejercicio, intente averiguar cómo se\(\{\alpha_n, \beta_n\}\) relacionan los viejos coeficientes con los nuevos coeficientes)\(\{f_n\}\).
Si\(\{f_n\}\) se conocen los coeficientes de Fourier, entonces se\(f(x)\) pueden calcular usando la fórmula anterior. Lo contrario también es cierto: dado\(f(x)\), podemos determinar los coeficientes de Fourier. Para ver cómo, observar que\[\int_{-a/2}^{a/2} dx \; e^{-2\pi i m x/a}\, e^{2\pi i n x/a} = a\, \delta_{mn}\quad \mathrm{for}\;m, n \in \mathbb{Z},\] donde\(\delta_{mn}\) está el delta de Kronecker, definido como:\[\delta_{mn} = \left\{\begin{array}{ll}1, & \textrm{if}\; m = n\\ 0, & \mathrm{if}\;m\ne n.\end{array}\right.\] Debido a esta propiedad, se dice que el conjunto de funciones\(\exp(2\pi i n x / a)\), con valores enteros de\(n\), son funciones ortogonales. (No entraremos en los detalles ahora, pero el término “ortogonalidad” se usa aquí con el mismo significado que en el álgebra vectorial, donde\(\vec{v}_1, \vec{v}_2, \dots\) se dice que un conjunto de vectores es “ortogonal” si es\(\vec{v}_m \cdot \vec{v}_n = 0\) para\(m\ne n\).) De ahí\[\begin{align} \int_{-a/2}^{\,a/2} dx\; e^{-2\pi i m x/a} \;f(x) &= \, \int_{-a/2}^{\,a/2} dx\; e^{-2\pi i m x/a} \left[\sum_{n=-\infty}^\infty e^{2\pi i n x/a}\, f_n\right] \\ &= \sum_{n=-\infty}^\infty \, \int_{-a/2}^{\,a/2} dx\; e^{-2\pi i m x/a} \, e^{2\pi i n x/a} \;f_n \\ &= \sum_{n=-\infty}^\infty \, a\, \delta_{mn} \, f_n \\ &= a \,f_m.\end{align}\] que el procedimiento de multiplicar por\(\exp(-2\pi i m x/a)\) e integrar sobre\(x\) actúa como un tamiz, filtrando todos los demás componentes de Fourier\(f(x)\) y manteniendo solo el que tiene el índice coincidente\(m\). Así, llegamos a un par de relaciones que expresan\(f(x)\) en términos de sus componentes de Fourier, y viceversa:
Teorema\(\PageIndex{1}\)
\[\left\{\;\;\begin{array}{rl}f(x) &= \displaystyle \, \sum_{n=-\infty}^\infty e^{i k_n x}\, f_n \\ f_n &= \displaystyle\,\frac{1}{a} \int_{-a/2}^{\,a/2} dx\; e^{-i k_n x}\, f(x)\end{array}\;\;\right. \quad\quad\mathrm{where}\;\; k_n \equiv \frac{2\pi n}{a} \label{fseries-relations}\]
Los números reales\(k_n\) se llaman números de onda. Forman un conjunto discreto, con uno para cada componente de Fourier. En la jerga física, decimos que los números de onda están “cuantificados” a múltiplos enteros de\(\Delta k \equiv 2\pi/a.\)
Ejemplo: Serie de Fourier de una onda cuadrada
Para tener una idea de cómo se comporta la serie de Fourier, veamos una onda cuadrada: una función que toma solo dos valores\(+1\) o\(-1\), saltando entre los dos valores a intervalos periódicos. Dentro de un periodo, la función está\[f(x) = \left\{\begin{array}{ll}-1, & -a/2 \le x < 0 \\ +1, & \quad\;\;\; 0 \le x < a/2.\end{array}\right.\] Conectando esto a la relación de Fourier, y haciendo las integrales directas, da los coeficientes de Fourier\[\begin{align} f_n &= -i \, \frac{\left[\sin\left(n \pi/2\right)\right]^2}{n\pi/2 } \\ &= \left\{\begin{array}{cl} -2i/n\pi ,& n \; \mathrm{odd} \\ 0,& n \; \mathrm{even}. \end{array} \right.\end{align}\] Como se puede ver, los coeficientes de Fourier se vuelven pequeños para grandes\(n\). Podemos escribir la serie de Fourier como\[f(x) \; \leftrightarrow \; \sum_{n=1,3,5,\dots} \frac{4\sin(2\pi n x / a)}{n \pi}.\] Si esta serie infinita se trunca a un número finito de términos, obtenemos una aproximación a\(f(x)\). Como se muestra en la siguiente figura, la aproximación se vuelve cada vez mejor a medida que se incluyen más términos.
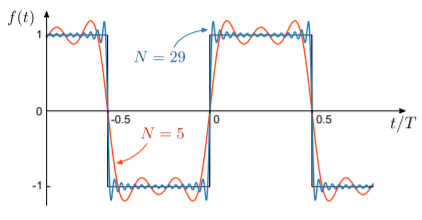
Una consecuencia divertida del resultado anterior es que podemos usarlo para derivar una expansión en serie para\(\pi\). Si establecemos\(x = a/4\),\[f(a/4) = 1 = \frac{4}{\pi} \left[\sin(\pi/2) + \frac{1}{3}\sin(3\pi/2) + \frac{1}{5}\sin(5\pi/2) + \cdots\right],\] y por lo tanto\[\pi = 4 \left(1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots\right).\]


