10.2: Transformadas de Fourier

La serie de Fourier se aplica a las funciones periódicas definidas a lo largo del intervalo\(-a/2 \le x < a/2\). Pero el concepto puede generalizarse a funciones definidas a lo largo de toda la línea real\(x \in \mathbb{R}\),, si tomamos el límite\(a \rightarrow \infty\) con cuidado.

Supongamos que tenemos una función\(f\) definida sobre toda la línea real,\(x \in \mathbb{R}\), tal que\(f(x) \rightarrow 0\) para\(x \rightarrow \pm\infty\). Imagínese que hay una familia de funciones periódicas\(\big\{f_a(x) \,\big|\, a \in\mathbb{R}^+\big\}\), tales que\(f_a(x)\) tiene periodicidad\(a\), y enfoques\(f(x)\) en el límite\(a\rightarrow \infty\). Esto se ilustra en la siguiente figura:

Figura\(\PageIndex{1}\)

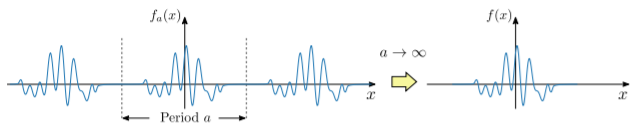
En términos matemáticos,\[f(x) = \lim_{a \rightarrow \infty} f_a(x), \;\;\;\text{where}\;\; f_a(x+a) = f_a(x).\] Dado que\(f_a\) es periódico, se puede expandir como una serie de Fourier:\[f_a(x) = \sum_{n=-\infty}^\infty e^{i k_n x}\, f_{an}, \quad\mathrm{where}\;\; k_n = n\Delta k, \;\; \Delta k = \frac{2\pi}{a}.\] Aquí,\(f_{an}\) denota el\(n\) -ésimo complejo coeficiente de Fourier de la función\(f_a(x)\). Obsérvese que cada coeficiente de Fourier depende implícitamente de la periodicidad\(a\).

Como\(a \rightarrow \infty\), el cuántico de onda-número\(\Delta k\) va a cero, y el conjunto de discretos\(k_n\) se convierte en un continuo. Durante este proceso, cada coeficiente individual de Fourier\(f_{an}\) va a cero, porque cada vez hay más componentes de Fourier en las proximidades de cada\(k\) valor, y cada componente de Fourier aporta menos. Esto implica que podemos sustituir la suma discreta por una integral. Para lograr esto, primero multiplicamos el summand por un factor de\((\Delta k/2\pi) / (\Delta k/2\pi) = 1\):\[f(x) = \lim_{a\rightarrow \infty} \left[\;\,\sum_{n=-\infty}^\infty \frac{\Delta k}{2\pi} \, e^{i k_n x}\, \left(\frac{2\pi \,f_{an}}{\Delta k} \right)\;\,\right].\] (En caso de que se lo esté preguntando, la elección de\(2\pi\) los factores es esencialmente arbitraria; estamos siguiendo la convención habitual). Además, definimos\[F(k) \equiv \lim_{a \rightarrow \infty} \left[\frac{2\pi\, f_{an}}{\Delta k}\right]_{k = k_n}.\] En el\(a \rightarrow \infty\) límite, el\(f_{an}\) en el numerador y el\(\Delta k\) en el denominador ambos van a cero, pero si su relación permanece finita, podemos convertir la suma de Fourier en la siguiente integral:\[f(x) = \int_{-\infty}^{\infty} \frac{dk}{2\pi} \, e^{i k x}\, F(k). \label{Fk}\]

Las relaciones de Fourier

La función\(F(k)\) en la Ec. \(\eqref{Fk}\)se llama la transformada de Fourier de\(f(x)\). Así como lo hemos expresado\(f(x)\) en términos de\(F(k)\), también podemos expresarlo\(F(k)\) en términos de\(f(x)\). Para ello, aplicamos el\(a \rightarrow \infty\) límite a la relación inversa para la serie de Fourier en la Ec. (10.1.13):\[\begin{align} F(k_n) &= \lim_{a\rightarrow \infty} \frac{2 \pi\, f_{an}}{\Delta k} \\ &= \lim_{a\rightarrow \infty} \frac{2 \pi}{2\pi/a}\, \left(\frac{1}{a} \int_{-a/2}^{a/2} dx\; e^{-i k_n x}\right) \\ &= \int_{-\infty}^\infty dx\; e^{-i kx}\, f(x).\end{align}\] De ahí que lleguemos a un par de ecuaciones llamadas las relaciones de Fourier:

Definición: Relaciones de Fourier

\[\begin{align}\left\{\;\;\begin{aligned}F(k) &= \;\int_{-\infty}^\infty dx\; e^{-ikx}\, f(x) &&\text{(Fourier transform)}\\ f(x) &= \int_{-\infty}^\infty \frac{dk}{2\pi}\; e^{ikx}\, F(k)&&\text{(Inverse Fourier transform).}\end{aligned}\;\;\right. \end{align} \label{fourier-relations}\]

La primera ecuación es la transformada de Fourier, y la segunda ecuación se llama transformada inversa de Fourier.

Hay diferencias notables entre las dos fórmulas. Primero, hay un factor de\(1/2\pi\) aparece al lado\(dk\), pero no tal factor para\(dx\); esto es una cuestión de convención, ligada a nuestra definición anterior de\(F(k)\). Segundo, la integral sobre\(x\) contiene un factor de\(e^{-ikx}\) pero la integral sobre\(k\) contiene un factor de\(e^{ikx}\). Una forma de recordar qué ecuación tiene el signo positivo en el exponente es interpretar la ecuación de la transformada inversa de Fourier (que tiene la forma de una integral sobre\(k\)) como el límite continuo de una suma sobre ondas complejas. En esta suma,\(F(k)\) juega el papel de los coeficientes de serie, y por convención las ondas complejas tienen la forma\(\exp(ikx)\) (ver Sección 6.3).

Como se señala en la Sección 10.1, se asume que todas las funciones que tratamos son integrables al cuadrado. Esto incluye las\(f_a\) funciones utilizadas para definir la transformada de Fourier. En el\(a \rightarrow \infty\) límite, esto implica que estamos tratando funciones tales que\[\int_{-\infty}^{\infty} dx\; \big|\,f(x)\,\big|^2\;\;\text{exists and is finite}.\]

Un ejemplo sencillo

Considera la función\[f(x) = \left\{\begin{array}{cl}e^{-\eta x}, & x \ge 0 \\ 0, & x < 0,\end{array}\right. \qquad \eta \in \mathbb{R}^+.\] For\(x < 0\), esta es una función que decae exponencialmente, y para\(x < 0\) ella es idénticamente cero. El parámetro real\(\eta\) se llama constante de decaimiento; para\(\eta > 0\), la función se\(f(x)\) desvanece\(x \rightarrow +\infty\) y, por lo tanto, se puede demostrar que es integrable al cuadrado. Los valores más grandes\(\eta\) corresponden a una decaimiento exponencial más rápido.

La transformada de Fourier se puede encontrar calculando directamente la integral de Fourier:\[F(k) \;=\; \;\int_{0}^\infty dx\; e^{-i kx}\, e^{-\kappa x} \;=\; \frac{-i}{k - i \eta}.\] Es útil graficar la magnitud cuadrada de la transformada de Fourier,\(|F(k)|^2\), contra\(k\). Esto se llama el espectro de Fourier de\(f(x)\). En este caso,\[\big|\,F(k)\,\big|^2 = \frac{1}{k^2 + \eta^2}.\]

Figura\(\PageIndex{2}\)

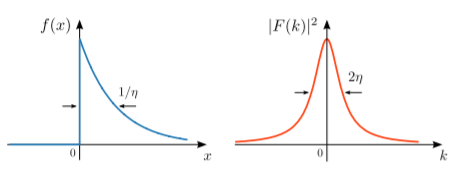
El espectro de Fourier se muestra en la subgráfica derecha de arriba. Consiste en un pico centrado en\(k = 0\), formando una curva llamada lorentziana. El ancho del lorentziano depende de la constante de decaimiento de la función original\(\eta\). Para los pequeños\(\eta\), es decir, débilmente en descomposición\(f(x)\), el pico es estrecho; para los grandes\(\eta\), es decir, que se descomponen rápidamente\(f(x)\), el pico es ancho.

Podemos cuantificar el ancho del lorentziano definiendo el ancho completo a la mitad del máximo (FWHM) —el ancho de la curva a la mitad del valor de su máximo. En este caso, el máximo de la curva lorentziana ocurre en\(k=0\) y tiene el valor de\(1/\eta^2\). El medio máximo,\(1/2\eta^2\), ocurre cuando\(\delta k = \pm \eta\). De ahí que la constante de decaimiento de la función original\(\eta\),, sea directamente proporcional al FWHM del espectro de Fourier, que es\(2\eta\).

Para concluir este ejemplo, evaluemos la transformada inversa de Fourier:\[f(x) \; = \; -i\int_{-\infty}^\infty \frac{dk}{2\pi} \; \frac{e^{i kx}}{k-i\eta}.\] Esto se puede resolver mediante la integración de contornos. La continuación analítica del integrando tiene un polo simple en\(k = i\eta\). Porque\(x < 0\), el numerador\(\exp(ikx)\) desaparece lejos del origen en el medio plano inferior, por lo que cerramos el contorno de abajo. Esto no encierra polo, por lo que la integral es cero. Para\(x > 0\), el numerador desaparece lejos del origen en el medio plano superior, por lo que cerramos el contorno arriba, con un arco en sentido antihorario, y el teorema del residuo da\[f(x) = \left(\frac{-i}{2\pi}\right) \, \left(2\pi i\right) \, \mathrm{Res}\left[ \frac{e^{ikx}}{k-i\eta}\right]_{k=i\eta} = e^{-\eta x} \qquad(x > 0),\] como se esperaba.