11.3: La causalidad y la función del verde en el dominio del tiempo

Última actualización
Guardar como PDF

Page ID: 126059

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Intentemos convertir la ecuación (11.2.13) en una función de Green en el dominio del tiempo usando la transformada inversa de Fourier:\[\begin{align} G(x,x';t-t') &= \int_{-\infty}^\infty \frac{d\omega}{2\pi} \, e^{-i\omega (t-t')} \, G(x,x'; \omega) \\ \nonumber &= \int_{-\infty}^\infty d\omega \, \frac{e^{i\omega \left[|x-x'| - (t-t')\right]}}{4\pi i\omega}\qquad (?!?) \nonumber\end{align}\] Hay un problema en la última línea: la integral corre sobre la\(\omega\) línea real, sin embargo, el integrando tiene un polo en\(\omega = 0\), en el eje real, haciendo el integral mal definido.

Para resolver esto, redefinimos\(G(x,x';\omega)\) como una integral sobre un contorno deformado\(\Gamma\):\[G(x,x';t-t') \equiv \int_\Gamma d\omega \, \frac{e^{i\omega \left[|x-x'| - (t-t')\right]}}{4\pi i\omega}.\] Escogeremos el contorno deformado de una manera muy específica, que resulta ser la elección que satisface la causalidad. Como se muestra en la subtrama izquierda de la figura de abajo, corre a lo largo del eje real, pero salta por encima del polo en el origen.

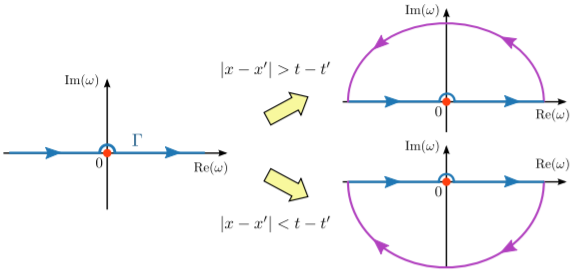
La integral se puede resolver ya sea cerrando el contorno en el medio plano superior, o bien en el medio plano inferior. Si cerramos el contorno arriba, entonces el contorno de bucle no encierra el polo, y por lo tanto\(G(x,x';t-t') = 0\). Según el lema de Jordania, debemos hacer esto si el exponente en el integrando obedece\[|x-x'| - (t-t') > 0 \quad \Rightarrow \quad |x-x'| > t-t'.\] Esta desigualdad se satisface en dos casos: ya sea (i)\(t < t'\) (en cuyo caso la desigualdad se satisface para todos\(x,x'\) porque\(|x-x'|\) es estrictamente no negativa), o (ii )\(t > t'\) pero el valor de\(t-t'\) es menor que\(|x-x'|\). Para comprender el significado físico de estos dos casos, recuerde que\(G(x,x';t-t')\) representa el campo en posición\(x\) y tiempo\(t\) resultante de un pulso en el punto espacio-tiempo\((x',t')\). Así, el caso (i) corresponde a los tiempos que ocurren antes del pulso, y el caso (ii) corresponde a los tiempos que ocurren después del pulso pero demasiado lejos de la ubicación del pulso para que una onda alcance en el tiempo.

Para el otro caso,\(|x-x'| - (t-t') < 0\), el teorema del residuo da\[G(x,x';t-t') = -1/2.\] El diagrama espacio-tiempo a continuación resume los resultados anteriores:

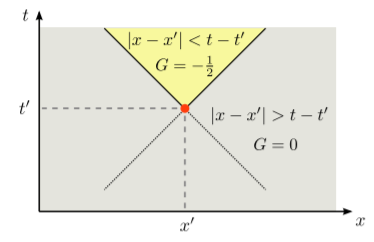
Las funciones de onda de dominio de tiempo resultantes se pueden escribir como\[\psi(x,t) = \int_{-\infty}^\infty dx' \int_{-\infty}^\infty dt' \left[-\frac{1}{2}\,\Theta(t-t' - |x-x'|)\right] f(x',t'),\] donde\(\Theta\) denota la función de paso de unidad. En otras palabras, la función de onda en cada punto espacio-tiempo\((x,t)\) recibe la misma contribución de las fuentes\(f(x',t')\) en los puntos espacio-temporales que se\((x',t')\) encuentran dentro del “cono de luz pasado”.