Saltar al contenido principal
LibreTexts Español

16.1: Introducción

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128365
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Explicar cómo los humanos pueden caracterizar el sonido

    Antes de profundizar demasiado en la física del cálculo de ondas sonoras (estudiar cosas como el Efecto Doppler, por ejemplo), abordemos algunos conceptos básicos del sonido. El sonido es una onda, una onda longitudinal de presión que viaja a través de medios compresibles (es decir, sólidos, líquidos, gaseosos o hechos de plasma). No hay sonido en un vacío; por definición, un vacío es un espacio libre de cualquier partícula o materia. Así que ahí en el vacío, no hay medios a través de los cuales puedan viajar las ondas sonoras. A continuación se presentan algunas características del sonido:

    • El sonido viaja en ondas longitudinales. Cuando se dibujan estas también se llaman ondas sinusoidales, un ejemplo visual de las cuales se muestra en (cubriremos esto con más detalle en una sección diferente).
    • Las ondas sonoras tienen frecuencia; es decir, el tono de los sonidos sube o baja.
    • La amplitud de un sonido determina su volumen (volumen).
    • El tono es una medida de la calidad de una onda de sonido.
    • El sonido viaja más rápido en un meduim caliente, o en un sólido. También viaja más rápido al nivel del mar (donde la presión del aire es mayor).
    • La intensidad del sonido es la energía transmitida sobre un área determinada. La intensidad es una medida de la frecuencia del sonido.
    • El ultrasonido utiliza ondas sonoras con altas frecuencias para ver cosas normalmente difíciles de detectar, como tumores. Los animales, como murciélagos y delfines, usan ultrasonido (ecolocalización) para navegar y localizar cosas. Los barcos también utilizan una técnica similar (conocida como SONAR) para localizar cosas bajo el agua. (Este punto se discutirá más a fondo en un Átomo más avanzado.)

    Percepción sonora

    Cada onda sonora tiene propiedades que definen su frecuencia, como longitud de onda, amplitud e intensidad. El cálculo de estas propiedades está fuera del alcance de este átomo y se abordará más adelante. Por ahora, es importante conocer los fundamentos del sonido. Al igual que con las ondas de luz, las frecuencias de sonido tienen un rango. Cada criatura viviente tiene un nivel diferente de percepción sonora. Por ejemplo, considere los siguientes ejemplos de rangos de sonido (en Hz, Hertz):

    • Humanos 20 — 20,000 Hz
    • Perros 50 — 45,000 Hz
    • Murciélagos 20 — 120,000 Hz

    Por esta comparación, los humanos tienen una percepción sonora relativamente baja.

    Velocidad de sonido

    imagen

    Rompiendo la barrera del sonido: Esta imagen familiar es de un plano que se mueve más rápido que la velocidad del sonido.

    Como se mencionó anteriormente, la velocidad a la que viaja el sonido depende de los medios por los que viaja el sonido. Es mucho más rápido en un sólido que en un líquido o gas. La fórmula general para calcular la velocidad del sonido se da como:

    \[\mathrm{c=\sqrt{\dfrac{K}{ρ}},}\]

    donde K es el coeficiente de rigidez del material (también llamado Módulo Bulk) y p es la densidad del material. Esto lo examinaremos más a fondo en otra sección. Generalmente, la expresión 'más rápido que la velocidad del sonido' se refiere a 344 m/s. es una imagen que demuestra un plano que se mueve más rápido que la velocidad del sonido. Esta medición general se toma al nivel del mar, a una temperatura de 21 grados Celsius en condiciones atmosféricas normales.

    Frecuencia de ondas sonoras

    La frecuencia es el número de ocurrencias de un evento repetitivo por unidad de tiempo. La percepción de la frecuencia se llama tono.

    objetivos de aprendizaje

    • Relacionar la frecuencia con la longitud de onda y la velocidad del sonido

    Las ondas sonoras, como todas las demás ondas, tienen una propiedad llamada frecuencia. La frecuencia es el número de ocurrencias de un evento repetitivo por unidad de tiempo. La percepción de la frecuencia se llama tono.

    La frecuencia depende de la longitud de onda y la velocidad del sonido. Se calcula con la siguiente ecuación:\(\mathrm{f=\frac{v_s}{λ}}\)

    Esta figura,, muestra cómo se conecta la frecuencia a la longitud de onda.

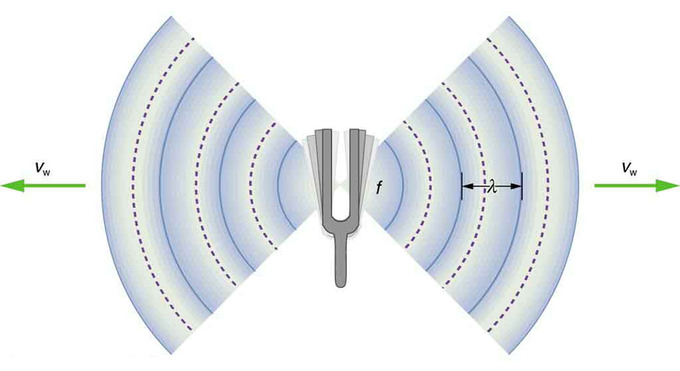
    imagen

    Frecuencia: Una onda sonora emana de una fuente que vibra a una frecuencia f, se propaga a v y tiene una longitud de onda λ.

    Alternativamente, puedes usar la frecuencia y la longitud de onda para encontrar la velocidad del sonido en un medio específico. Recuerda que el sonido viaja a diferentes velocidades en diferentes medios; el sonido se mueve más rápido a través de un sólido. La siguiente ecuación se utiliza para encontrar la velocidad específica del sonido, y a menudo es más fácil de usar que la ecuación de velocidad estándar del sonido: vs=f*λv_s=f*\ lambda

    Un periodo es la duración de un ciclo de un evento repetitivo, y es el recíproco o inverso de la frecuencia. La siguiente animación muestra diferentes frecuencias y sus periodos, de menor a mayor.

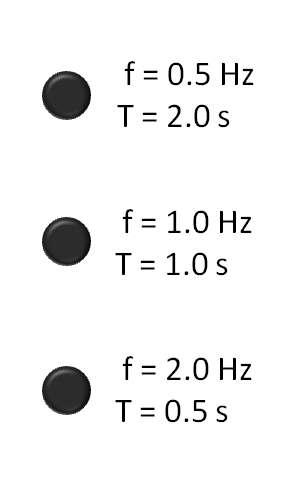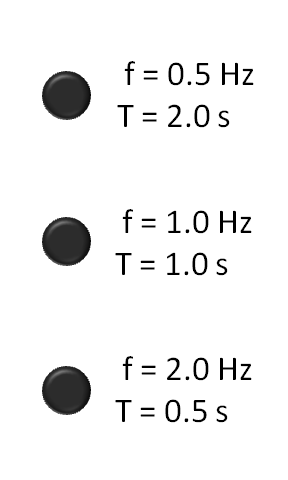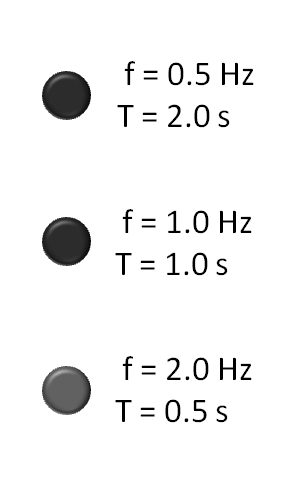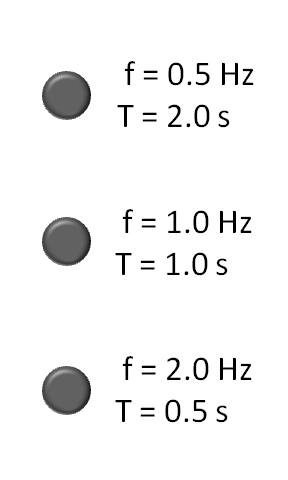
    imagen

    Animación de frecuencia: Tres luces intermitentes, desde la frecuencia más baja (arriba) hasta la frecuencia más alta (abajo). f es la frecuencia en hercios (Hz); o el número de ciclos por segundo. T es el periodo en segundos (s); o el número de segundos por ciclo. T y f son recíprocos.

    Hertz

    La unidad de frecuencia SI se llama Hertz, denotada Hz. Un hercio se define como el número de ciclos por segundo. Por ejemplo, 100 Hz significa 100 ciclos por segundo.

    Diferentes especies pueden escuchar diferentes rangos de frecuencia. Los humanos solo pueden escuchar de 20 Hz a 20,000 Hz, mientras que los perros pueden escuchar hasta 60,000 Hz. Los murciélagos pueden escuchar los rangos más altos, hasta 120,000 Hz. Los murciélagos utilizan esta súper audición, o ultrasonido, para localizar objetos y presas. Al rebotar ondas sonoras de otro objeto y escuchar cuánto tiempo tarda el sonido en hacerles eco, son capaces de aproximar la distancia entre ellos y el objeto. Esto se llama ecolocalización.

    Producción de sonido: Cuerdas Vibrantes y Columnas de Aire

    El sonido puede ser producido por muchos dispositivos diferentes. Una cuerda vibrante o una columna de aire pueden crear música y tener propiedades únicas.

    objetivos de aprendizaje

    • Calcular la frecuencia de la onda sonora producida por la cuerda y una columna de aire

    El sonido puede ser producido de muchas maneras, por muchos instrumentos y dispositivos diferentes. Una cuerda vibrante o una columna de aire pueden hacer música interesante y es bueno entender la física detrás de ambas.

    Cuerdas Vibrantes

    Son muchos los instrumentos que producen sonido a base de cuerdas. Guitarras, violonchelos, pianos y muchos otros ejemplos. Estos sonidos son producidos por ondas estacionarias en las cuerdas. Estas ondas y sus frecuencias son constantes, y por lo tanto el sonido y el tono producidos por ellas es constante. Esta figura muestra una visual de una onda estacionaria en una cuerda: La velocidad de la onda es proporcional a la raíz de la tensión de la cuerda, e inversamente proporcional a la raíz de la densidad de la cuerda, mostrada por la siguiente ecuación\(\mathrm{v=\sqrt{\frac{T}{μ}}}\) Pitch, y la forma en que se percibe el sonido depende de la frecuencia del onda de sonido. Usando la velocidad de onda, puedes encontrar la frecuencia usando esta ecuación:\(\mathrm{f=\frac{v}{2L}}\), donde L es la longitud de la cuerda.

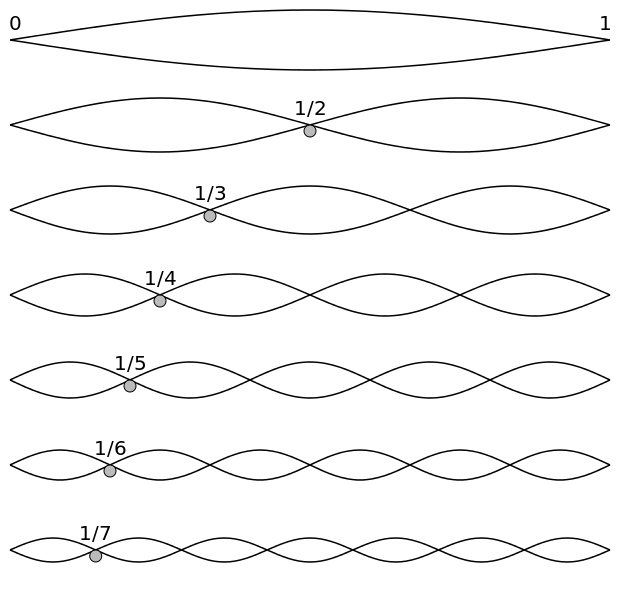
    imagen

    Ondas estacionarias en una cuerda: Vibración, ondas estacionarias en una cuerda. El fundamental y los primeros 6 armónicos forman una serie armónica.

    Columnas de aire

    Muchos instrumentos hacen música al provocar una vibración a una columna de aire en un resonador. Estos suelen llamarse instrumentos de viento. Ejemplos de estos son flautas, grabadoras y saxofones. Están abiertas en ambos extremos, o bien cerradas en un extremo y abiertas en el otro. El tono del sonido es una función de la frecuencia. Son muchos los factores que intervienen en encontrar la frecuencia. Comencemos con los tubos que están cerrados en un extremo y abiertos en el otro.

    Tubos de Aire Cerrados:El desplazamiento máximo del aire ocurre en el extremo abierto del tubo, y se llama el antinodo. El movimiento del aire está restringido en el extremo cerrado, y no hay desplazamiento, y esto se llama el nodo. La distancia desde el nodo hasta el antinodo es 1/4 de la longitud de una longitud de onda, e igual a la longitud del tubo, como se muestra en esta ecuación:\(\mathrm{λ=4L}\) Esto también se puede ver en esta figura: La frecuencia es igual a la velocidad del sonido en el aire dividida por la longitud de onda, o:\(\mathrm{f=\frac{v_w}{λ}=\frac{v_w}{4L}}\), donde v w es la velocidad del sonido en el aire, que aprendimos a encontrar en un átomo anterior.

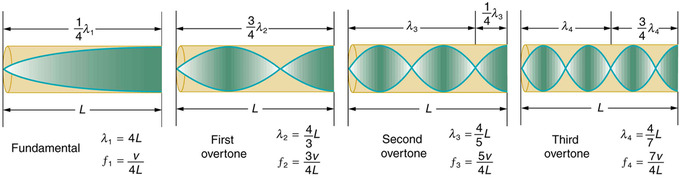
    imagen

    Una columna de aire en un tubo cerrado en un extremo: El fundamental y tres armónicos más bajos para un tubo cerrado en un extremo. Todos tienen desplazamientos máximos de aire en el extremo abierto y ninguno en el extremo cerrado.

    Tubos de aire abierto:Los tubos de aire también pueden estar abiertos en ambos extremos. Son muy similares a los que hablamos anteriormente, pero hay un antinodo en ambos extremos, ya que ambos están abiertos, como se muestra en esta figura: Dado que hay un antinodo en ambos extremos, podemos ver que la longitud de una longitud de onda se encuentra por esta ecuación:\(\mathrm{λ=2L}\) Y la frecuencia se puede encontrar en el siguiente ecuación:\(\mathrm{f=\frac{v_w}{λ}=\frac{v_w}{2L}}\)

    Calidad de Sonido

    La calidad del sonido es una evaluación de la precisión o la disfrutabilidad de cómo se percibe un sonido.

    Habilidades para Desarrollar

    • Identificar factores que influyen en la calidad de sonido de una reproducción de música

    La calidad del sonido es una evaluación de la precisión o la disfrutabilidad de cómo se percibe un sonido. Se puede medir objetiva o subjetivamente. ¿Cuál es la diferencia? La medición objetiva se toma cuando se utilizan herramientas para medir la precisión. La medición subjetiva es más una opinión. Cuando los oyentes humanos escuchan un sonido y lo comparan con otro sonido que han escuchado, y deciden cuál disfrutan más, esta es una medición subjetiva de la calidad del sonido.

    Calidad de sonido musical

    La calidad de sonido de la música en vivo se conoce como su tono. ¿Qué hace que este tono? ¿Por qué la misma nota que se toca en un piano suena diferente de esa nota que se toca en una flauta, o una guitarra? Cuando escuchas una nota, en su mayoría escuchas la frecuencia fundamental. Pero hay otros armónicos presentes. Se escuchan estos, pero son mucho, mucho más tenues que la frecuencia fundamental, o principal. Estos se llaman armónicos.

    Cada instrumento tiene una mezcla diferente de estos armónicos, y es por ello que los sonidos de notas similares suenan diferentes. La calidad de este sonido depende de estos armónicos para no hacerse cargo de lo que estás escuchando. Los armónicos y la frecuencia fundamental se combinan para hacer una frecuencia única que escuchas, que se ilustra en.

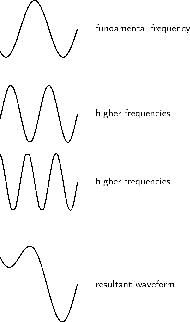
    imagen

    Frecuencias de sonido: La calidad de un tono depende de su mezcla de armónicos.

    Calidad de sonido reproducida

    La calidad de sonido de una reproducción de música depende de muchos factores. Estos incluyen:

    • Equipo de grabación
    • Procesamiento y masterización
    • Equipo de reproducción
    • Ambiente de escucha

    Cuando escuchas una grabación de música, estás escuchando no solo la música en sí, sino también cualquier interferencia que pueda haber sido grabada erróneamente también. La forma más simple de audio almacenado digitalmente es PCM.

    A medida que las muestras se colocan más juntas en el tiempo, se pueden reproducir frecuencias más altas. Según el teorema de muestreo, cualquier señal con ancho de banda B puede ser perfectamente descrita por más de 2B muestras por segundo. El audio debe ser muestreado por encima de 40kHz: 44.1kHz para grabaciones de CD y 48kHz para grabaciones de DVD.

    La cantidad de espacio requerido para almacenar PCM depende del número de bits por muestra, el número de muestras por segundo y el número de canales. Para el audio de CD, esto es 44,100 muestras por segundo, 16 bits por muestra y 2 canales para audio estéreo que conducen a 1,411,200 bits por segundo.

    Velocidad del sonido

    La velocidad del sonido es la distancia recorrida en una unidad de tiempo por una onda sonora a través de un medio elástico, y generalmente se da como 344 m/s.

    Habilidades para Desarrollar

    • Calcular la velocidad del sonido a partir de las propiedades de los medios

    Velocidad de Soud

    La velocidad del sonido es la distancia recorrida en una unidad de tiempo por una onda sonora a través de un medio elástico. Este medio puede ser un sólido, líquido, gas o incluso plasma. La velocidad del sonido depende de las propiedades de los medios por los que viaja el sonido. El valor general dado para la velocidad del sonido es la velocidad de una onda sonora en el aire, a nivel del mar, a presión atmosférica normal; ese número es 344 m/s, sin embargo, este número no es constante. El sonido viaja más rápido en un sólido que en un líquido, y más rápido en un líquido que en un gas.

    Tipos de Ondas de Sonido: Compresión y Cizalla

    Hay dos tipos diferentes de ondas sonoras: ondas de compresión y ondas cortantes. Las ondas de compresión pueden viajar a través de cualquier medio, pero las ondas cortantes solo pueden viajar a través de sólidos La velocidad de una onda de compresión está determinada por la capacidad de compresión del medio, el módulo de cizallamiento y la densidad, mientras que la velocidad de la onda de cizallamiento solo está determinada por el módulo de cizallamiento y la densidad. El módulo de cizallamiento es una medida de la elasticidad o rigidez de un material. Calcular esto está fuera del alcance de este átomo, pero hay tablas que le indican su valor para los materiales.

    Cálculo de la velocidad del sonido

    La velocidad del sonido generalmente se denota por cc, y se puede usar una ecuación general para calcularlo. Esto se llama la ecuación de Newton-Laplace: C=√KρC=KρK es el coeficiente de rigidez, y p es la densidad de los medios. A partir de esta ecuación, es fácil ver que la velocidad del sonido aumentará con la rigidez y disminuirá con la densidad. Esta es una ecuación muy general, hay derivaciones más específicas, por ejemplo:

    La velocidad del sonido en el aire al nivel del mar viene dada por la siguiente ecuación:\(\mathrm{c_{air}=331\frac{m}{s} \times \sqrt{\frac{T}{273K}}}\) T es la temperatura en Kelvin.

    Número Mach

    Es posible que hayas escuchado antes el término número de Mach en relación con la velocidad de las naves espaciales o los jets. Esta es una relación de la velocidad de un objeto en relación con la velocidad del sonido. El número Mach viene dado por la siguiente ecuación adimensional:\(\mathrm{M=\frac{v}{a}}\) — Mach numberv — Velocidad del objeto a — Velocidad del sonido en medio. Si algo viaja a la velocidad del sonido, eso haría que la ecuación sea igual a 1, y se puede denotar como Mach 1. muestra un jet que está viajando a la velocidad del sonido o más rápido. El cono de vapor se hace justo antes de que alcance la velocidad del sonido y es causado por una caída repentina en la presión del aire.

    imagen

    Más rápido que la velocidad del sonido: Se trata de un jet que está a punto de romper la barrera del sonido.

    Puntos Clave

    • El sonido viaja en ondas sinusoidales longitudinales.
    • Los humanos pueden caracterizar el sonido por frecuencia, amplitud y tono.
    • La velocidad a la que viaja el sonido depende de los medios por los que viaja el sonido. Se puede calcular utilizando:\(\mathrm{c=\sqrt{\frac{K}{ρ}}}\), donde K es el coeficiente de rigidez del material (también llamado el Módulo Bulk) y p es la densidad del material.
    • La frecuencia depende de la longitud de onda y la velocidad del sonido. Se calcula con la siguiente ecuación:\(\mathrm{f=\frac{v_s}{λ}}\)
    • Un periodo es la duración de un ciclo de un evento repetitivo, y es el recíproco o inverso de la frecuencia.
    • La unidad de frecuencia SI se llama Hertz, denotada Hz. Un hercio se define como el número de ciclos por segundo. Por ejemplo, 100 Hz significa 100 ciclos por segundo.
    • La frecuencia, y por lo tanto el tono de un instrumento de cuerda depende de la velocidad de la onda sonora y de la longitud de la cuerda. La frecuencia se encuentra por:\(\mathrm{f=\frac{\sqrt{\frac{T}{μ}}}{2L}.}\)
    • El sonido en un tubo de aire que se cierra en un extremo se encuentra mediante la siguiente ecuación:\(\mathrm{f=\frac{v_w}{λ}=\frac{v_w}{4L}}\).
    • El sonido en un tubo de aire que está abierto en un extremo se encuentra por la siguiente ecuación:\(\mathrm{f=\frac{v_w}{λ}=\frac{v_w}{2L}}\).
    • La medición objetiva se toma cuando se utilizan herramientas para medir la precisión. La medición subjetiva es más una opinión. Cuando los oyentes humanos escuchan un sonido y lo comparan con otro sonido que han escuchado, y deciden cuál disfrutan más, esta es una medición subjetiva de la calidad del sonido.
    • La calidad de sonido de la música en vivo se conoce como su tono. Cuando escuchas una nota, en su mayoría escuchas la frecuencia fundamental. Pero hay otros armónicos presentes. Se escuchan estos, pero son mucho, mucho más tenues que la frecuencia fundamental, o principal. Estos se llaman armónicos.
    • La calidad de sonido de una reproducción de música depende de muchos factores. Estos incluyen: equipo de grabación, procesamiento y masterización, equipo de reproducción e incluso ambiente de escucha.
    • El sonido puede viajar a través de cualquier material compresible. Estos medios pueden ser sólidos, líquidos, gaseosos o incluso plasma.
    • La velocidad del sonido depende de las propiedades del material por el que viaja. Viajará más rápido a través de un sólido que de un líquido, y más rápido a través de un líquido que de un gas.
    • El número general dado para la velocidad del sonido se calcula al nivel del mar, en el aire, a presión atmosférica normal. Ese valor es 344 m/s.

    Términos Clave

    • frecuencia: El cociente del número de veces n un fenómeno periódico se produce a lo largo del tiempo t en que ocurre:\(\mathrm{f = \frac{n}{t}}\).
    • Hertz: Medición de la frecuencia del sonido.
    • media: Término general para diferentes tipos de materiales.
    • periodo: La duración de un ciclo en un evento repetitivo.
    • node: Punto sobre una ola donde no hay desplazamiento.
    • antinodo: región de amplitud máxima situada entre nodos adyacentes de un cuerpo vibratorio, como una cuerda
    • Medición subjetiva: A partir de una comparación con una experiencia previa, opinión.
    • Medición objetiva: Tomada por herramientas para medir la precisión.
    • elasticidad: La propiedad en virtud de la cual un material deformado bajo la carga puede recuperar sus dimensiones originales cuando se descarga
    • kelvin: en el Sistema Internacional de Unidades, la unidad base de la temperatura termodinámica; 1/273.16 de la temperatura termodinámica del punto triple del agua; simbolizada como K

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 16.1: Introducción is shared under a not declared license and was authored, remixed, and/or curated by Boundless.