18.1: Visión general

objetivos de aprendizaje

• Explicar la relación entre el potencial eléctrico y el campo eléctrico

La relación entre el potencial eléctrico y el campo es similar a la existente entre el potencial gravitacional y el campo en que el potencial es una propiedad del campo que describe la acción del campo sobre un objeto (ver).

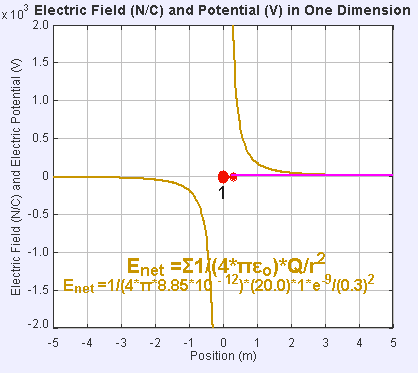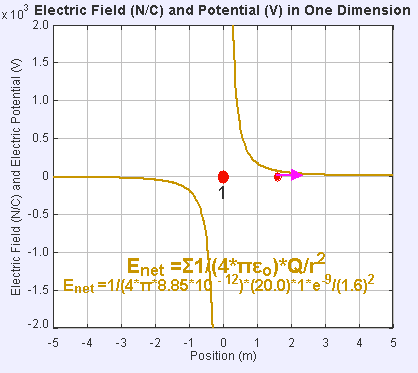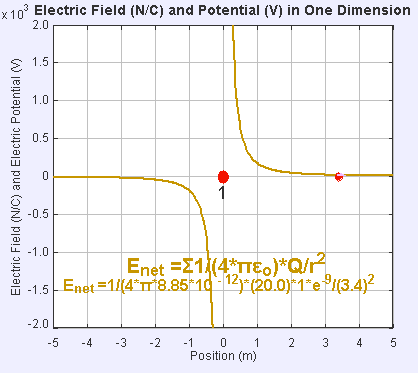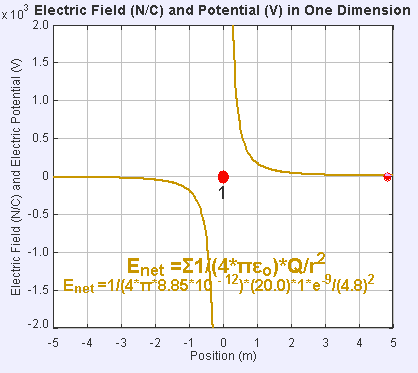
Campo eléctrico y potencial en una dimensión: La presencia de un campo eléctrico alrededor de la carga puntual estática (punto rojo grande) crea una diferencia de potencial, haciendo que la carga de prueba (punto rojo pequeño) experimente una fuerza y se mueva.

El campo eléctrico es como cualquier otro campo vectorial, ejerce una fuerza basada en un estímulo y tiene unidades de fuerza por estímulo inverso. En el caso de un campo eléctrico el estímulo es carga, y así las unidades son NC ^-1. Es decir, el campo eléctrico es una medida de fuerza por unidad de carga.

El potencial eléctrico en un punto es el cociente de la energía potencial de cualquier partícula cargada en esa ubicación dividido por la carga de esa partícula. Sus unidades son JC ^-1. Así, el potencial eléctrico es una medida de energía por unidad de carga.

En cuanto a las unidades, el potencial eléctrico y la carga están estrechamente relacionados. Comparten un factor común de Coulombs inversos (C ^-1), mientras que la fuerza y la energía solo difieren por un factor de distancia (la energía es producto de la fuerza por distancia).

Así, para un campo uniforme, la relación entre el campo eléctrico (E), la diferencia de potencial entre los puntos A y B (Δ) y la distancia entre los puntos A y B (d) es:

\[\mathrm { E } = - \frac { \Delta \phi } { \mathrm { d } }\]

El coeficiente -1 surge de la repulsión de cargas positivas: una carga positiva será empujada lejos de la placa cargada positivamente, y hacia una ubicación de mayor voltaje.

La ecuación anterior es una relación algebraica para un campo uniforme. En un sentido más puro, sin asumir uniformidad de campo, el campo eléctrico es el gradiente del potencial eléctrico en la dirección de x:

\[\mathrm { E } _ { \mathrm{ x } } = - \dfrac { \mathrm { dV } } { \mathrm { dx } }\]

Esto puede derivarse de principios básicos. Dado que ∆P=W (cambio en la energía de una carga equivale al trabajo realizado en esa carga), una aplicación de la ley de conservación de energía, podemos sustituir ∆P y W por otros términos. ∆P puede ser sustituido por su definición como el producto de carga (q) y el diferencial de potencial (dV). Entonces podemos reemplazar W con su definición como el producto de q, campo eléctrico (E), y el diferencial de distancia en la dirección x (dx):

\[\mathrm { qdV } = - q \mathrm { E } _ { \mathrm { xdx } } \]

Al dividir ambos lados de la ecuación por q se obtiene la ecuación anterior.

Energía de potencial eléctrico y diferencia de potencial

La energía potencial eléctrica es el resultado de fuerzas entre cargas; la diferencia de potencial es la energía necesaria para mover una carga del punto A al B.

objetivos de aprendizaje

• Calcular la energía potencial entre las cargas

La energía eléctrica potencial es un tipo de energía potencial que resulta de las fuerzas de Coulomb. Se mide en julios y depende del posicionamiento de las partículas cargadas entre sí, así como de la magnitud de sus respectivas cargas.

La energía potencial (U _E) entre las cargas q y Q se puede calcular en función de la distancia entre las cargas (r):

\[\mathrm { U } _ { \mathrm { E } } ( \mathrm { r } ) = \frac { \mathrm { q } Q } { 4 \pi \epsilon _ { 0 } \mathrm { r } }\]

Si hay tres o más cargas, se puede modificar la fórmula anterior para que se sumen las energías potenciales entre todas las cargas. Consideremos, por ejemplo, el caso que involucra cargos Q ₁, Q ₂ y Q ₃:

\[\mathrm { U } _ { \mathrm { E } } = \frac { 1 } { 4 \pi \epsilon _ { 0 \mathrm { r } } } \left( \frac { \mathrm { Q } _ { 1 } \mathrm { Q } _ { 2 } } { \mathrm { r } 12 } + \frac { \mathrm { Q } _ { 2 } \mathrm { Q } _ { 3 } } { \mathrm { r } 23 } + \frac { \mathrm { Q } _ { 1 } \mathrm { Q } _ { 3 } } { \mathrm { r } 13 } \right)\]

En este ejemplo, r ₁₂ representa la distancia entre Q ₁ y Q ₂, r ₂₃ representa la distancia entre Q ₂ y Q ₃, y r ₁₃ representa la distancia entre Q ₁ y _Q3. La fórmula anterior se puede modificar para cualquier número de cargos.

Diferencia de potencial

La diferencia de potencial, o voltaje, es la diferencia en la energía potencial eléctrica entre dos puntos. Se denota por ∆V y tiene unidades de voltios, o julios por Coulomb.

Diferencia de potencial eléctrico: Una breve descripción de la diferencia de potencial eléctrico y la energía potencial eléctrica para estudiantes principiantes de física.

Voltaje denota el trabajo por unidad de carga que debe realizarse contra un campo eléctrico estático para mover una carga de un punto a otro. Puede representar una fuente de energía, o energía perdida, almacenada o usada. El voltaje también se define de tal manera que las cargas negativas son arrastradas hacia voltajes más altos, mientras que las cargas positivas se mueven hacia voltajes más bajos. Por lo tanto, la corriente en los cables fluye de mayores a menores voltajes.

La diferencia de potencial es independiente del camino tomado de un punto a otro, y puede ser medida por cualquiera de una serie de instrumentos. Estos incluyen el voltímetro, el potenciómetro y el osciloscopio. Normalmente se mide en circuitos, y en tales situaciones se puede calcular usando la Ley de Ohm, que se cubrirá en un átomo posterior.

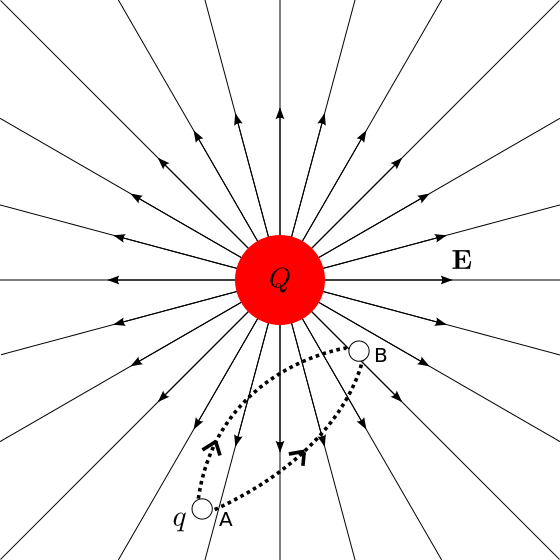
Diferencia de potencial en un campo estático: Cuando una carga q se mueve del punto A al punto B, la diferencia de potencial es independiente del camino tomado.

Campo eléctrico y potencial eléctrico cambiante

El campo eléctrico es el gradiente de potencial, que depende inversamente de la distancia de un punto de interés dado de una carga.

objetivos de aprendizaje

• Calcular el potencial eléctrico creado por una distribución de carga de valor constante

Cualquier carga creará un campo vectorial alrededor de sí mismo (conocido como campo eléctrico). El campo eléctrico es el gradiente de potencial, que depende inversamente de la distancia de un punto de interés dado de una carga. Colocar una segunda carga en el sistema (una “carga de prueba”) da como resultado que las dos cargas experimenten una fuerza (las unidades del campo son Newtons, una medida de fuerza por Coulomb), lo que hace que las cargas se muevan una con relación a la otra. Es más fácil modelar las interacciones entre dos cargas de tal manera que una se considere estacionaria mientras la carga de prueba se mueve.

A medida que se mueve la carga de prueba, el potencial entre ésta y otra carga cambia, al igual que el campo eléctrico. La relación entre potencial y campo (E) es diferencial: el campo eléctrico es el gradiente de potencial (V) en la dirección x. Esto se puede representar como:

\[\mathrm { E } _ { \mathrm { x } } = - \dfrac { \mathrm { d } \mathrm { V } } { \mathrm { d } \mathrm { x } }\]

Líneas Equipotenciales: Una carga puntual aislada Q con sus líneas de campo eléctrico (azules) y líneas equipotenciales (verdes)

Así, a medida que la carga de prueba se mueve en la dirección x, la tasa de su cambio de potencial es el valor del campo eléctrico.

El instante antes de que se mueva la carga de prueba, su energía potencial está en un máximo, y su energía cinética es 0. Para cualquier carga de valor constante (Q), el potencial a cierta distancia de él (r) se puede calcular a partir de la siguiente ecuación:

\[\mathrm { V } _ { \mathrm { E } } = \dfrac { 1 } { 4 \pi \epsilon _ { 0 } } \dfrac { Q } { \mathrm { r } }\]

donde ε ₀ es la constante eléctrica, también conocida como permitividad del espacio libre. El acercamiento y alejamiento de la carga da como resultado un cambio de potencial; la relación entre distancia y potencial es inversa.

Para una carga puntual, el potencial será constante para todos los puntos a cierta distancia radial. Múltiples puntos de un mismo potencial se conocen como equipotenciales. En el caso de campos creados por una sola carga puntual, todos los puntos de cualquier círculo centrado alrededor de la carga puntual serán equipotenciales, como se ilustra en.

muestra que cuando múltiples cargas crean un campo, las líneas equipotenciales adquieren una forma irregular. Esto se debe a que los campos creados por cada carga se superponen, por lo que el potencial se incrementa en cualquier punto relativo al que habría surgido de una u otra carga.

Potenciales y conductores cargados

El potencial eléctrico dentro de un conductor cargado es igual a cero, pero se puede calcular como un valor distinto de cero fuera de un conductor cargado.

objetivos de aprendizaje

• Determinar el potencial eléctrico dentro y fuera de un conductor cargado

Cuando un conductor se carga, esa carga se distribuye a través de su superficie hasta alcanzar el equilibrio electrostático. Su superficie es equipotencial.

Todos los puntos dentro de un conductor cargado experimentan un campo eléctrico de 0. Esto se debe a que las líneas de campo de las cargas en la superficie del conductor se oponen entre sí por igual. Sin embargo, teniendo el campo eléctrico igual a cero en todos los puntos dentro de un conductor, el potencial eléctrico dentro de un conductor no es necesariamente igual a cero para todos los puntos dentro de ese mismo conductor. Esto se puede probar relacionando el campo eléctrico y el potencial.

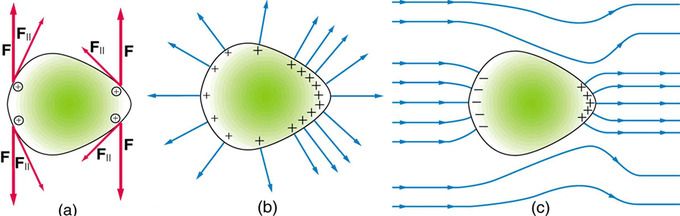
Carga eléctrica en un punto afilado de un conductor: Las fuerzas repulsivas hacia la superficie más pronunciada de la derecha apuntan más hacia afuera que a lo largo de la superficie del conductor.

Dado que el trabajo es la diferencia en las energías potenciales finales e iniciales (∆U), podemos relacionar esta diferencia con el producto puntual de la fuerza en cada distancia infinitesimal l a lo largo de la trayectoria entre los puntos dentro del conductor:

\ Delta\ mathrm {U} = -\ int _ {\ mathrm {i}} ^ {f}\ vec {\ mathrm {F}}\ cdot\ mathrm {d}\ vec {}

Esta es la ecuación para el trabajo, con ∆U sustituido en lugar de W. Reescribiendo U como producto de carga (q) y diferencia de potencial (V), y fuerza como producto de carga y campo eléctrico (E), podemos afirmar:

\[\Delta ( \mathrm { qV } ) = - \int _ { \mathrm { i } } ^ { \mathrm { f } } ( \mathrm { qE } ) \cdot \mathrm { d } \vec { \mathrm { l } }\]

Dividiendo ambos lados por el término común de q, simplificamos la ecuación para:

\[\Delta \mathrm { V } = - \int _ { \mathrm { i } } ^ { \mathrm { f } } \vec { \mathrm { E } } \cdot \mathrm { d } \vec { \mathrm { l } }\]

Finalmente derivamos la ecuación:

\[\mathrm { d } \mathrm { V } = - \vec { \mathrm { E } } \cdot \mathrm { d } \vec { \mathrm { l } } = 0\]

Así podemos concluir que, dado que el campo eléctrico es constantemente 0 para cualquier ubicación dentro del conductor cargado, la diferencia de potencial en ese mismo volumen necesita ser constante e igual a 0.

Por otro lado, para puntos fuera de un conductor, el potencial es distinto de cero y puede definirse por la misma ecuación, según el campo y la distancia del conductor.

Campo Eléctrico Uniforme

Un campo eléctrico que es uniforme es aquel que alcanza la consistencia inalcanzable de ser constante en todo momento.

objetivos de aprendizaje

• Describir las propiedades y aproximaciones del campo eléctrico uniforme

Un campo uniforme es aquel en el que el campo eléctrico es constante en todo momento. Al igual que la llamada “superficie sin fricción” en mecánica, el campo uniforme es una situación ideal pero irreal que hace que los cálculos sean más simples. Las ecuaciones que involucran campos eléctricos no uniformes requieren el uso de cálculo diferencial.

La uniformidad en un campo eléctrico se puede aproximar colocando dos placas conductoras paralelas entre sí y creando una diferencia de potencial entre ellas. En tal caso habrá ligeras variaciones en el campo cerca de sus bordes, pero será aproximadamente constante en todas las demás áreas.

La ecuación para la magnitud de un campo eléctrico uniforme es:

\[\mathrm { E } = \dfrac { - \Delta \phi } { \mathrm { d } }\]

donde E es el campo, Δ es la diferencia de potencial entre las placas, y d es la distancia entre las placas. El coeficiente de -1 surge del hecho de que las cargas positivas se repelen, y así una carga positiva será empujada lejos de la placa positiva y en una dirección opuesta a la del voltaje creciente.

La uniformidad de un campo eléctrico permite un cálculo simple del trabajo realizado cuando se mueve una carga de prueba a través de él. Para el caso de que una carga positiva q se mueva de un punto A con cierto potencial (V ₁) a un punto B con otro potencial (V ₂), esa ecuación es:

\[\mathrm { W } = - \mathrm { q } \left( \mathrm { V } _ { 2 } - \mathrm { V } _ { 1 } \right)\]

La diferencia (V ₂ -V ₁) también se puede representar como ∆V o V _AB. En campos uniformes también es sencillo relacionar ∆V con la intensidad de campo y la distancia (d) entre los puntos A y B:

\[\mathbf { V } _ { \mathrm { AB } } = \mathrm { E } \mathrm { d }\]

Relaciones dentro de un campo eléctrico uniforme: En esta imagen, se definen Trabajo (W), intensidad de campo (E) y diferencia de potencial (∆V) para los puntos A y B dentro de los constructos de un campo potencial uniforme entre las placas positiva y negativa.

Conservación de Energía

La energía se conserva en el movimiento de una partícula cargada a través de un campo eléctrico, como lo es en cualquier otra situación física.

objetivos de aprendizaje

• Formular principio de conservación de energía para una partícula cargada en un campo eléctrico

La energía se conserva en el movimiento de una partícula cargada a través de un campo eléctrico, como lo es en cualquier otra situación física. Este fenómeno puede expresarse como la igualdad de energías cinéticas sumadas (E _kin) y potencial eléctrico (E _el):

\[( \mathrm { E } _ { \mathrm { kin } } + \mathrm { E } _ { \mathrm { el } } ) _ { \text { initial } } = ( \mathrm { E } _ { \mathrm { kin } } + \mathrm { E } _ { \mathrm { el } } ) _ { \mathrm { final } }\]

Dada una carga de prueba estacionaria en cierta ubicación, un campo eléctrico aplicado hará que la carga se mueva hacia un extremo u otro, dependiendo de la carga (las cargas de prueba positivas se moverán en la dirección del campo; las cargas negativas se moverán en la dirección opuesta). En todos los casos, una carga se moverá naturalmente de un área de mayor energía potencial a un área de menor energía potencial.

En el instante en que se aplica el campo, la carga de prueba inmóvil tiene 0 energía cinética, y su energía potencial eléctrica está en un máximo. Después de ese momento, la carga se acelera, y su energía cinética (del movimiento) aumenta a medida que disminuye su energía potencial. A lo largo de este tiempo, la suma de energías potenciales y cinéticas se mantiene constante.

Otra forma de expresar la ecuación anterior es:

\[( \dfrac { 1 } { 2 } \mathrm { mv } ^ { 2 } + \mathrm { U }) _ { \text { initial } } = ( \dfrac { 1 } { 2 } \mathrm { mv } ^ { 2 } + \mathrm { U } ) _ { \mathrm { final } }\]

donde m y v son la masa y velocidad del electrón, respectivamente, y U es la energía potencial eléctrica. U se puede calcular de la siguiente manera:

\[\mathrm { U } = \mathrm{q _ { 0 }} \mathrm { V } = \mathrm { k } \dfrac { \mathrm { q } _ { 0 } \mathrm { q } } { \mathrm { r } }\]

donde V es la diferencia de potencial, k es una constante, q ₀ es una carga de prueba, q es otra carga y r es la distancia entre las cargas.

Los términos involucrados en la fórmula para la conservación de la energía pueden reescribirse de muchas maneras, pero todas las expresiones se basan en la simple premisa de equiparar las sumas inicial y final de la energía cinética y potencial.

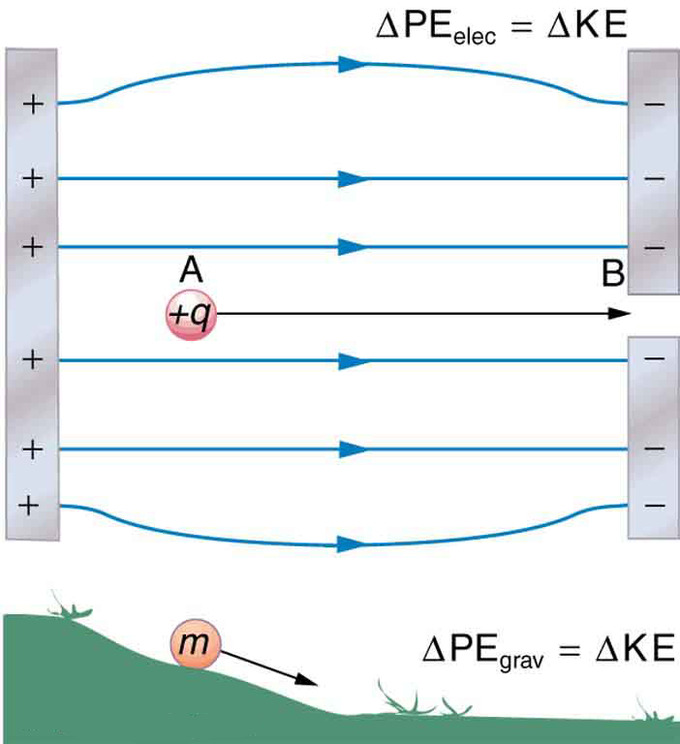
Similitudes entre la actividad de los campos gravitacional y eléctrico sobre un objeto: La carga, +q, se mueve hacia abajo del campo eléctrico de la misma manera que el objeto, m, se mueve cuesta abajo de la colina. En ambos casos, la partícula en movimiento pasa de un estado de energía potencial superior a uno más bajo.

El electrón-voltios

El electrón voltio es una unidad de energía útil en la física de cargas elementales y electricidad.

objetivos de aprendizaje

• Convertir entre electrón voltios y unidades SI de energía

Visión general

El electrón voltio, simbolizado como eV y a veces escrito como electronvoltio, es una unidad de energía útil en la física de cargas elementales y electricidad.

El electrón voltio se define como la cantidad de energía ganada o perdida por la carga de un electrón movido a través de una diferencia de potencial eléctrico de un voltio. Como tal, es igual al producto de un voltio (1 J/C) y una carga elemental, dándole un valor en julios aproximadamente igual a 1.602×10 ^-19 J.

No una unidad SI en sí misma, el electrón voltio se volvió útil a través de la experimentación. Los científicos que trabajan con aceleradores electrostáticos de partículas comúnmente usaron la relación entre energía (E), carga (q) y diferencia de potencial (V) en su trabajo:

\[\mathrm { E } = \mathrm { q } \mathrm { V }\]

Todos los cálculos de energía de la ecuación anterior se cuantificaron como múltiplos de la carga elemental, q, para un voltaje dado, y así surgió el uso común del electrón voltio como unidad de medida.

Momentum

Tanto los electrón-voltios como el impulso son medidas de energía, y los dos están relacionados en la física de alta energía. Aplicar una diferencia de potencial a un electrón le da energía, que se manifiesta en movimiento del electrón a través de él. Dado que el electrón tiene tanto masa como velocidad, tiene momentum. Dividir electrón-voltios por una constante con unidades de velocidad da como resultado un impulso.

Masa

Dado que la masa es equivalente a la energía, el electrón voltio puede medir la masa. En física de partículas, la ecuación ^E=mC2 se puede reorganizar para resolver la masa:

\[\mathrm { m } = \dfrac { \mathrm { E } } { \mathrm { c } ^ { 2 } } \]

Longitud de onda

La energía E, la frecuencia v y la longitud de onda λ de un fotón están relacionadas por

\[\mathrm { E } ( \mathrm { eV } ) = \mathrm { hv } = \dfrac { \mathrm { hc } } { \lambda }\]

donde h es la constante de Planck y c es la velocidad de la luz. Así, un fotón con una longitud de onda de 532 nm (luz verde) tendría una energía de aproximadamente 2.33 eV. De igual manera, 1 eV correspondería a un fotón infrarrojo de longitud de onda 1240 nm, y así sucesivamente.

Energía de fotones en el espectro visible: Relación entre longitud de onda y energía expresada en electrón-voltios.

Temperatura

En la física del plasma, el electrón voltio puede ser utilizado como una unidad de temperatura. Para convertir a Kelvins, simplemente divide el valor de 1 eV (en julios) por la constante de Boltzmann (1.3806505 (24) ×10 ^-23 J/K).

Momentos dipolares

El momento dipolo eléctrico es una medida de polaridad en un sistema.

objetivos de aprendizaje

• Relacionar el momento dipolo eléctrico con la polaridad en un sistema

El momento dipolo eléctrico es una medida de polaridad, que es la separación de cargas positivas y negativas en un sistema. Se mide en unidades de culomb-metros (C m). Hay muchos tipos diferentes de momentos dipolares, incluidos los momentos dipolares eléctricos, los momentos dipolares magnéticos y los momentos dipolares topológicos.

Entre el subconjunto de momentos dipolares eléctricos se encuentran los momentos dipolares de transición, los momentos dipolares moleculares, los momentos dipolares de enlace y los momentos dipolares eléctricos de electrones. Para los fines de este átomo nos centraremos en una amplia visión general del momento dipolo eléctrico en situaciones estáticas.

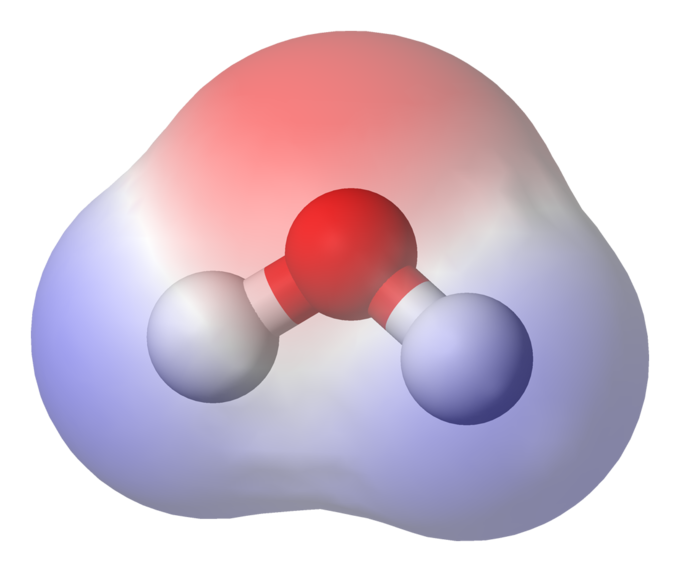
Momento Dipolo Molecular en Agua: Esta molécula de agua (H ₂ O) tiene una alta densidad de electrones (denotada por el sombreado rojo) cerca del átomo O rojo. Más cerca de los átomos H blancos, hay una baja densidad de electrones. Por lo tanto, la molécula es un dipolo, con negatividad cerca del O y positividad más cercana a los átomos de H.

Definición

Fundamentalmente, para el caso de cargas puntuales con valores +q y -q, se puede definir un momento dipolar eléctrico (p) como el producto vectorial de las cargas y el vector de desplazamiento d:

\[\mathrm { p } = \mathrm { q } \mathrm { d }\]

El vector de desplazamiento es el vector con una magnitud igual a la distancia entre las cargas y una dirección que apunta desde la carga negativa a la carga positiva. Es esencialmente intercambiable con la variable “radio” en muchas otras ecuaciones (como las que determinan las fuerzas gravitacionales y electrostáticas), excepto que incluye el factor de dirección.

Torque

Todos los dipolos experimentarán una fuerza torsional, o torque, cuando se colocan en campos eléctricos externos. Este par gira el dipolo para alinearlo con el campo. Es provocado por la necesidad de minimizar la energía potencial. El par (τ) se puede calcular como el producto cruzado del momento dipolo eléctrico y el campo eléctrico (E), asumiendo que E es espacialmente uniforme:

\[\tau = \mathrm { p } \times \mathrm { E }\]

Puntos Clave

• El campo eléctrico es una medida de fuerza por unidad de carga; el potencial eléctrico es una medida de energía por unidad de carga.
• Para un campo uniforme, la relación entre el campo eléctrico (E), la diferencia de potencial entre los puntos A y B (Δ), y la distancia entre los puntos A y B (d) es:\(\mathrm { E } = - \frac { \Delta \phi } { \mathrm { d } }\) Si el campo no es uniforme, se requiere cálculo para resolver.
• Potencial es una propiedad del campo que describe la acción del campo sobre un objeto.
• La energía eléctrica potencial es un tipo de energía potencial que resulta de las fuerzas de Coulomb. La energía potencial (UE) entre las cargas q y Q se puede calcular en función de la distancia entre las cargas (r):\(\mathrm { U } _ { \mathrm { E } } ( \mathrm { r } ) = \frac { \mathrm { q } Q } { 4 \pi \epsilon _ { 0 } \mathrm { r } }\).
• La fórmula de energía potencial puede ser modificada por potencial entre muchas cargas, siempre y cuando se consideren las interacciones de cada carga con cualquier otra carga en el sistema. Por ejemplo, el potencial entre tres cargas se puede resolver usando la siguiente fórmula:\(\mathrm { U } _ { \mathrm { E } } = \frac { 1 } { 4 \pi \epsilon _ { 0}\mathrm { r } } \left( \frac { Q _ { 1 } Q _ { 2 } } { \mathrm { r } 12 } + \frac { \mathrm { Q } _ { 2 } \mathrm { Q } _ { 3 } } { \mathrm { r } 23 } + \frac { \mathrm { Q } _ { 1 } Q _ { 3 } } { \mathrm { r } 13 } \right)\).
• La diferencia de potencial, o voltaje, es la diferencia en la energía potencial eléctrica entre dos puntos. Se denota por ∆V y tiene unidades de voltios, o julios por Coulomb.
• Para cualquier carga de valor constante (Q), el potencial (VE) a cierta distancia de él (r) se puede calcular a partir de la ecuación:\(\mathrm { V } _ { \mathrm { E } } = \frac { 1 } { 4 \pi \epsilon _ { 0 } } \frac { \mathrm { Q } } { \mathrm { r } }\) Dónde\(\mathrm{ε_0}\) está la constante eléctrica, también conocida como permitividad del espacio libre.
• Para una carga puntual, el potencial será constante para todos los puntos a cierta distancia radial. Múltiples puntos de un mismo potencial se conocen como equipotenciales.
• Cuando múltiples cargas crean un campo, las líneas equipotenciales adquieren una forma irregular. Esto se debe a que los campos creados por cada carga se superponen, por lo que el potencial se incrementa en cualquier punto relativo al que habría surgido de una u otra carga.
• El potencial eléctrico (∆V) y el campo (E) se relacionan de acuerdo con la integral:\(\mathrm{\Delta V = - \int _ { i } ^ { f } \vec { E } \cdot d \vec { l }}\) donde l es la distancia entre dos puntos entre los que se encuentra la diferencia de potencial.
• Dado que el campo eléctrico es constantemente 0 para cualquier ubicación dentro del conductor cargado, es imposible que la diferencia de potencial en ese mismo volumen tenga otro valor que no sea 0.
• Para los puntos fuera de un conductor, el potencial es distinto de cero y se puede calcular de acuerdo con el campo y la distancia desde el conductor.
• El campo eléctrico uniforme es una aproximación que permite realizar cálculos simples que no requieren cálculo diferencial. Cada campo tendrá al menos alguna irregularidad, aunque algunos pueden ser casi uniformes.
• La ecuación para la magnitud de un campo eléctrico uniforme es:\(\mathrm { E } = \frac { - \Delta \phi } { \mathrm { d } }\) donde E es el campo, Δ es la diferencia de potencial entre las placas, y d es la distancia entre las placas.
• Para el caso de que una carga positiva q se mueva de un punto A con cierto potencial (V ₁) a un punto B con otro potencial (V ₂), esa ecuación es:\( \mathrm { W } = - \mathrm { q } \left( \mathrm { V } _ { 2 } - \mathrm { V } _ { 1 } \right)\) La diferencia (V ₂ -V ₁) también se puede representar como ∆V o V _AB.
• En campos uniformes también es sencillo calcular la diferencia de potencial:\(\mathrm { V } _ { \mathrm { AB } } = \mathrm { E } \mathrm { d }\) En este caso, la intensidad de campo es E, y la distancia entre los puntos A y B es d.
• Dada una carga de prueba estacionaria en cierta ubicación, un campo eléctrico aplicado hará que la carga se mueva hacia un extremo u otro, dependiendo de la carga.
• Las cargas de prueba positivas se moverán en la dirección del campo; las cargas negativas se moverán en la dirección opuesta.
• En el instante en que se aplica el campo, la carga de prueba inmóvil tiene 0 energía cinética, y su energía potencial eléctrica está en un máximo. Entonces, la carga se acelera, y su energía cinética (del movimiento) aumenta a medida que disminuye su energía potencial.La suma de energías es siempre constante.
• La fórmula que ilustra la conservación de la energía puede escribirse de muchas maneras, pero todas las expresiones se basan en la simple premisa de equiparar las sumas inicial y final de la energía cinética y potencial.
• El electrón voltio se define como la cantidad de energía ganada o perdida por la carga de un electrón movido a través de una diferencia de potencial eléctrico de un voltio. Su valor es aproximadamente igual a 1.602×10 ^-19 J.
• El electrón voltio se volvió útil mediante la experimentación. Los científicos que trabajan con aceleradores electrostáticos de partículas comúnmente usaron la relación entre energía (E), carga (q) y diferencia de potencial (V) en su trabajo. Esta relación es:\(\mathrm{E=qV}\).
• Como energía, el electrón voltio se puede utilizar en muchos cálculos, incluidos el momento, la masa, la longitud de onda y la temperatura.
• Los momentos dipolares eléctricos se utilizan para medir la separación de cargas positivas y negativas (polaridad) en un sistema. Se miden en unidades de culomb-metros (C m).
• Para cargas puntuales con valores +q y -q, el momento dipolo eléctrico (p) puede definirse como:\(\mathrm{p=qd}\) donde q representa las cargas y d representa el vector de desplazamiento. El vector de desplazamiento tiene una magnitud de la distancia entre las cargas y una dirección de la carga negativa a la positiva.
• Todos los dipolos experimentarán un par que gira el dipolo para alinearlo con un campo eléctrico. Este par puede calcularse como el producto cruzado del momento dipolo eléctrico y el campo eléctrico.

Términos Clave

• campo eléctrico: Una región del espacio alrededor de una partícula cargada, o entre dos voltajes; ejerce una fuerza sobre los objetos cargados en su vecindad.
• potencial eléctrico: La energía potencial por unidad de carga en un punto en un campo eléctrico estático; voltaje.
• culomb: En el Sistema Internacional de Unidades, la unidad derivada de carga eléctrica; la cantidad de carga eléctrica transportada por una corriente de 1 amperio que fluye por 1 segundo. Símbolo: C
• energía potencial: La energía que tiene un objeto por su posición (en un campo gravitacional o eléctrico) o su condición (como resorte estirado o comprimido, como reactivo químico, o por tener masa en reposo)
• equipotencial: Una región cuyo cada punto tiene el mismo potencial.
• radial: Moviéndose a lo largo de un radio.
• campo eléctrico: Una región del espacio alrededor de una partícula cargada, o entre dos voltajes; ejerce una fuerza sobre los objetos cargados en su vecindad.
• trabajo: Una medida de la energía gastada en mover un objeto; más comúnmente, fuerza veces desplazamiento. No se realiza ningún trabajo si el objeto no se mueve.
• diferencia de potencial: La diferencia de energía potencial entre dos puntos en un campo eléctrico; la diferencia de carga entre dos puntos en un circuito eléctrico; voltaje.
• Energía cinética: La energía que posee un objeto por su movimiento, igual a la mitad de la masa del cuerpo por el cuadrado de su velocidad.
• acelerador de partículas: Un dispositivo que acelera las partículas cargadas eléctricamente a velocidades extremadamente altas, con el propósito de inducir reacciones de alta energía o producir radiación de alta energía.
• electrón voltio: Una unidad para medir la energía de partículas subatómicas; la energía igual a la alcanzada por un electrón que se mueve a través de una diferencia de potencial de un voltio. Equivalente a 1.6022 x 10-19 julios.
• momento dipolo: El producto vectorial de la carga en cualquiera de los polos de un dipolo y la distancia que los separa.
• vector: Una cantidad dirigida, una con magnitud y dirección; la entre dos puntos.
• par: Un efecto de rotación o torsión de una fuerza; (unidad SI newton-metro o Nm; unidad imperial pie-libra o ft-lb)

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• campo eléctrico. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/electric_field. Licencia: CC BY-SA: Atribución-CompartirIgual
• Potencial eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electric_potential. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electric_field. Licencia: CC BY-SA: Atribución-CompartirIgual
• potencial eléctrico. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/electric_potential. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Voltage. Licencia: CC BY-SA: Atribución-CompartirIgual
• Energía eléctrica potencial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electric_Potencial_energy. Licencia: CC BY-SA: Atribución-CompartirIgual
• energía potencial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Potencial%20Energía. Licencia: CC BY-SA: Atribución-CompartirIgual
• culombo. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/coulomb. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Definición electrostática de voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electrostatic_definition_of_voltage.svg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Diferencia de Potencial Eléctrico. Ubicado en: http://www.youtube.com/watch?v=jjwwb2yfytk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Líneas Equipotenciales. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42331/latest/. Licencia: CC BY: Atribución
• radial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/radial. Licencia: CC BY-SA: Atribución-CompartirIgual
• equipotencial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/equipotential. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Definición electrostática de voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electrostatic_definition_of_voltage.svg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Diferencia de Potencial Eléctrico. Ubicado en: http://www.youtube.com/watch?v=jjwwb2yfytk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Líneas Equipotenciales. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42331/latest/. Licencia: CC BY: Atribución
• potencial eléctrico. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/electric_potential. Licencia: CC BY-SA: Atribución-CompartirIgual
• campo eléctrico. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/electric_field. Licencia: CC BY-SA: Atribución-CompartirIgual
• Potencial eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electric_potential. Licencia: CC BY-SA: Atribución-CompartirIgual
• trabajo. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/work. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Definición electrostática de voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electrostatic_definition_of_voltage.svg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Diferencia de Potencial Eléctrico. Ubicado en: http://www.youtube.com/watch?v=jjwwb2yfytk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Líneas Equipotenciales. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42331/latest/. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 28 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42317/latest/?collection=col11406/latest. Licencia: CC BY: Atribución
• diferencia de potencial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/potential_difference. Licencia: CC BY-SA: Atribución-CompartirIgual
• campo eléctrico. Proporcionado por: Wikcionario. Ubicado en: http://en.wiktionary.org/wiki/electric_field. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electric_field. Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Potencial Eléctrico en un Campo Eléctrico Uniforme. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42326/latest/. Licencia: CC BY: Atribución
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Definición electrostática de voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electrostatic_definition_of_voltage.svg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Diferencia de Potencial Eléctrico. Ubicado en: http://www.youtube.com/watch?v=jjwwb2yfytk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Líneas Equipotenciales. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42331/latest/. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 28 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42317/latest/?collection=col11406/latest. Licencia: CC BY: Atribución
• OpenStax College, Potencial Eléctrico en un Campo Eléctrico Uniforme. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42326/latest/. Licencia: CC BY: Atribución
• Energía eléctrica potencial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electric_Potencial_energy. Licencia: CC BY-SA: Atribución-CompartirIgual
• diferencia de potencial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/potential_difference. Licencia: CC BY-SA: Atribución-CompartirIgual
• energía cinética. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Kinetic%20Energy. Licencia: CC BY-SA: Atribución-CompartirIgual
• energía potencial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Potencial%20Energía. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Definición electrostática de voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electrostatic_definition_of_voltage.svg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Diferencia de Potencial Eléctrico. Ubicado en: http://www.youtube.com/watch?v=jjwwb2yfytk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Líneas Equipotenciales. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42331/latest/. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 28 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42317/latest/?collection=col11406/latest. Licencia: CC BY: Atribución
• OpenStax College, Potencial Eléctrico en un Campo Eléctrico Uniforme. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42326/latest/. Licencia: CC BY: Atribución
• OpenStax College, Energía Potencial Eléctrica: Diferencia de Potencial. 3 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42324/latest/. Licencia: CC BY: Atribución
• diferencia de potencial. Proporcionado por: Wikcionario. Ubicado en: http://en.wiktionary.org/wiki/potential_difference. Licencia: CC BY-SA: Atribución-CompartirIgual
• Electronvoltio. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electronvolt. Licencia: CC BY-SA: Atribución-CompartirIgual
• electrón voltio. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/electron_volt. Licencia: CC BY-SA: Atribución-CompartirIgual
• acelerador de partículas. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/partícula_acelerador. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Definición electrostática de voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electrostatic_definition_of_voltage.svg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Diferencia de Potencial Eléctrico. Ubicado en: http://www.youtube.com/watch?v=jjwwb2yfytk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Líneas Equipotenciales. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42331/latest/. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 28 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42317/latest/?collection=col11406/latest. Licencia: CC BY: Atribución
• OpenStax College, Potencial Eléctrico en un Campo Eléctrico Uniforme. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42326/latest/. Licencia: CC BY: Atribución
• OpenStax College, Energía Potencial Eléctrica: Diferencia de Potencial. 3 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42324/latest/. Licencia: CC BY: Atribución
• Proporcionado por: Wikimedia. Ubicado en: http://upload.wikimedia.org/Wikipedia/commons/thumb/7/7f/Colors_in_eV.svg/605px-Colors_in_eV.svg.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Momento dipolo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Electric_Dipole_Moment. Licencia: CC BY-SA: Atribución-CompartirIgual
• par. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/torque. Licencia: CC BY-SA: Atribución-CompartirIgual
• vector. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/vector. Licencia: CC BY-SA: Atribución-CompartirIgual
• momento dipolo. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/dipole_moment. Licencia: CC BY-SA: Atribución-CompartirIgual
• Campo eléctrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electric_Field.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Definición electrostática de voltaje. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Electrostatic_definition_of_voltage.svg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Diferencia de Potencial Eléctrico. Ubicado en: http://www.youtube.com/watch?v=jjwwb2yfytk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Líneas Equipotenciales. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42331/latest/. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 28 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42317/latest/?collection=col11406/latest. Licencia: CC BY: Atribución
• OpenStax College, Potencial Eléctrico en un Campo Eléctrico Uniforme. 4 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42326/latest/. Licencia: CC BY: Atribución
• OpenStax College, Energía Potencial Eléctrica: Diferencia de Potencial. 3 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42324/latest/. Licencia: CC BY: Atribución
• Proporcionado por: Wikimedia. Ubicado en: http://upload.wikimedia.org/Wikipedia/commons/thumb/7/7f/Colors_in_eV.svg/605px-Colors_in_eV.svg.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Agua-Elpot-Transparentes-3D-Bolas. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Agua-Elpot-Transparent-3D-bolas.png. Licencia: CC BY-SA: Atribución-CompartirIgual