Saltar al contenido principal
LibreTexts Español

3.2: Vectores

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128438
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Componentes de un Vector

    Los vectores son representaciones geométricas de magnitud y dirección y pueden expresarse como flechas en dos o tres dimensiones.

    objetivos de aprendizaje

    • Contraste vectores bidimensionales y tridimensionales

    Los vectores son representaciones geométricas de magnitud y dirección que a menudo se representan por flechas rectas, comenzando en un punto en un eje de coordenadas y terminando en un punto diferente. Todos los vectores tienen una longitud, llamada la magnitud, que representa alguna calidad de interés para que el vector pueda compararse con otro vector. Los vectores, al ser flechas, también tienen una dirección. Esto los diferencia de los escalares, que son meros números sin dirección.

    Un vector se define por su magnitud y su orientación con respecto a un conjunto de coordenadas. A menudo es útil en el análisis de vectores para dividirlos en sus partes componentes. Para vectores bidimensionales, estos componentes son horizontales y verticales. Para los vectores tridimensionales, el componente de magnitud es el mismo, pero el componente de dirección se expresa en términos de xx, yy y zz.

    Descomponer un vector

    Para visualizar el proceso de descomposición de un vector en sus componentes, comience dibujando el vector desde el origen de un conjunto de coordenadas. A continuación, dibuja una línea recta desde el origen a lo largo del eje x hasta que la línea esté pareja con la punta del vector original. Este es el componente horizontal del vector. Para encontrar el componente vertical, dibuja una línea recta hacia arriba desde el final del vector horizontal hasta llegar a la punta del vector original. Deberías encontrar que tienes un triángulo rectángulo tal que el vector original sea la hipotenusa.

    Descomponer un vector en componentes horizontales y verticales es una técnica muy útil para comprender problemas físicos. Siempre que veas movimiento en ángulo, deberías pensar en él como un movimiento horizontal y vertical al mismo tiempo. Simplificar los vectores de esta manera puede acelerar los cálculos y ayudar a realizar un seguimiento del movimiento de los objetos.

    Escalares y Vectores: El señor Andersen explica las diferencias entre cantidades escalar y vectores. También utiliza una demostración para mostrar la importancia de los vectores y la adición de vectores.

    imagen

    Componentes de un Vector: El vector original, definido en relación con un conjunto de ejes. El componente horizontal se extiende desde el inicio del vector hasta su coordenada x más alejada. El componente vertical se extiende desde el eje x hasta el punto más vertical del vector. Juntos, los dos componentes y el vector forman un triángulo rectángulo.

    Escalares vs. vectores

    Los escalares son cantidades físicas representadas por un solo número, y los vectores se representan tanto por un número como por una dirección.

    objetivos de aprendizaje

    • Distinguir la diferencia entre las cantidades que representan los escalares y los vectores

    Las cantidades físicas generalmente se pueden colocar en dos categorías, vectores y escalares. Estas dos categorías están tipificadas por la información que requieren. Los vectores requieren dos piezas de información: la magnitud y la dirección. En contraste, los escalares requieren solo la magnitud. Los escalares pueden pensarse como números, mientras que los vectores deben pensarse más como flechas que apuntan en una dirección específica.

    imagen

    A Vector: Un ejemplo de un vector. Los vectores suelen estar representados por flechas con su longitud representando la magnitud y su dirección representada por la dirección que apunta la flecha.

    Los vectores requieren tanto una magnitud como una dirección. La magnitud de un vector es un número para comparar un vector con otro. En la interpretación geométrica de un vector el vector está representado por una flecha. La flecha tiene dos partes que la definen. Las dos partes son su longitud que representa la magnitud y su dirección con respecto a algún conjunto de ejes de coordenadas. Cuanto mayor sea la magnitud, más larga será la flecha. Conceptos físicos como desplazamiento, velocidad y aceleración son ejemplos de cantidades que pueden ser representadas por vectores. Cada una de estas cantidades tiene tanto una magnitud (qué tan lejos o qué tan rápido) como una dirección. Para especificar una dirección, debe haber algo a lo que la dirección sea relativa. Normalmente, este punto de referencia es un conjunto de ejes de coordenadas como el plano x-y.

    Los escalares difieren de los vectores en que no tienen una dirección. Los escalares se utilizan principalmente para representar cantidades físicas para las cuales una dirección no tiene sentido. Algunos ejemplos de estos son: masa, altura, longitud, volumen y área. Hablar de la dirección de estas cantidades no tiene sentido y por lo tanto no pueden expresarse como vectores.

    La diferencia entre Vectores y Escalares, Introducción y Fundamentos: Este video introduce la diferencia entre escalares y vectores. Se introducen ideas sobre magnitud y dirección y se dan ejemplos tanto de vectores como de escalares.

    Sumando y restando vectores gráficamente

    Los vectores pueden sumarse o restarse gráficamente colocándolos de extremo a extremo sobre un conjunto de ejes.

    objetivos de aprendizaje

    • Distinguir la diferencia entre las cantidades que representan los escalares y los vectores

    Sumando y restando vectores

    Una de las formas en que representar cantidades físicas como vectores facilita el análisis es la facilidad con la que se pueden agregar vectores entre sí. Dado que los vectores son visualizaciones gráficas, la suma y resta de vectores se puede hacer gráficamente.

    El método gráfico de adición de vectores también se conoce como el método de cabeza a cola. Para comenzar, dibuje un conjunto de ejes de coordenadas. A continuación, dibuje el primer vector con su cola (base) en el origen de los ejes de coordenadas. Para la suma de vectores no importa qué vector dibuje primero ya que la suma es conmutativa, pero para la resta asegúrate de que el vector que dibujas primero es del que estás restando. El siguiente paso es tomar el siguiente vector y dibujarlo de tal manera que su cola comience en la cabeza del vector anterior (el lado de la flecha). Continúe colocando cada vector a la cabeza del anterior hasta que se unan todos los vectores que desea agregar. Finalmente, dibuje una línea recta desde el origen hasta la cabeza del vector final en la cadena. Esta nueva línea es el resultado vectorial de sumar esos vectores juntos.

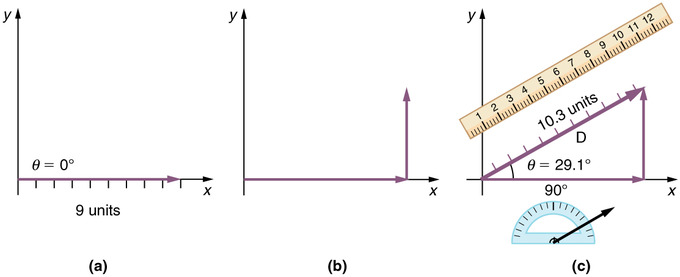
    imagen

    Adición gráfica de vectores: El método de adición de vectores de cabeza a cola requiere que coloque el primer vector a lo largo de un conjunto de ejes de coordenadas. A continuación, coloca la cola del siguiente vector sobre la cabeza del primero. Dibuja un nuevo vector desde el origen hasta la cabeza del último vector. Este nuevo vector es la suma de los dos originales.

    Adición de vectores Lección 1 de 2: Método de adición de cabeza a cola: Este video hace que los espectadores comiencen con la suma y resta de vectores. La primera lección muestra la adición gráfica mientras que el segundo video toma un enfoque más matemático y muestra la adición de vectores por componentes.

    Para restar vectores el método es similar. Asegúrate de que el primer vector que dibujas es el que se va a restar. Después, para restar un vector, proceder como si sumaran lo contrario de ese vector. En otras palabras, voltea el vector que se va a restar a través de los ejes y luego unirlo cola a cabeza como si agregara. Para voltear el vector, simplemente ponga su cabeza donde estaba su cola y su cola donde estaba su cabeza.

    Suma y resta de vectores mediante componentes

    A menudo es más sencillo sumar o restar vectores mediante el uso de sus componentes.

    objetivos de aprendizaje

    • Demostrar cómo sumar y restar vectores por componentes

    Uso de componentes para sumar y restar vectores

    Otra forma de agregar vectores es agregar los componentes. Anteriormente, vimos que los vectores se pueden expresar en términos de sus componentes horizontales y verticales. Para sumar vectores, simplemente expresar ambos en términos de sus componentes horizontal y vertical y luego sumar los componentes juntos.

    imagen

    Vector con Componentes Horizontales y Verticales: El vector en esta imagen tiene una magnitud de 10.3 unidades y una dirección de 29.1 grados por encima del eje x. Se puede descomponer en una parte horizontal y una parte vertical como se muestra.

    Por ejemplo, un vector con una longitud de 5 en un ángulo de 36.9 grados con respecto al eje horizontal tendrá una componente horizontal de 4 unidades y una componente vertical de 3 unidades. Si tuviéramos que sumar esto a otro vector de la misma magnitud y dirección, obtendríamos un vector el doble de largo en el mismo ángulo. Esto se puede ver sumando los componentes horizontales de los dos vectores\(\mathrm{(4+4)}\) y los dos componentes verticales (\(\mathrm{3+3}\)). Estas adiciones dan un nuevo vector con una componente horizontal de\(\mathrm{8(4+4)}\) y una componente vertical de\(\mathrm{6(3+3)}\). Para encontrar el vector resultante, simplemente coloque la cola del componente vertical en la cabeza (lado de la flecha) del componente horizontal y luego dibuje una línea desde el origen hasta la cabeza del componente vertical. Esta nueva línea es el vector resultante. Debe ser el doble de largo que el original, ya que ambos componentes son dos veces más grandes que antes.

    Para restar vectores por componentes, simplemente restar los dos componentes horizontales entre sí y hacer lo mismo con los componentes verticales. Después dibuja el vector resultante como hiciste en la parte anterior.

    Adición de vectores Lección 2 de 2: Cómo agregar vectores por componentes: Este video hace que los espectadores comiencen con la adición de vectores utilizando un enfoque matemático y muestra la adición de vectores por componentes.

    Multiplicar vectores por un escalar

    Multiplicar un vector por un escalar cambia la magnitud del vector pero no la dirección.

    objetivos de aprendizaje

    • Resumir la interacción entre vectores y escalares

    Visión general

    Aunque los vectores y escalares representan diferentes tipos de cantidades físicas, a veces es necesario que interactúen. Si bien agregar un escalar a un vector es imposible debido a sus diferentes dimensiones en el espacio, es posible multiplicar un vector por un escalar. Un escalar, sin embargo, no se puede multiplicar por un vector.

    Para multiplicar un vector por un escalar, simplemente multiplique los componentes similares, es decir, la magnitud del vector por la magnitud del escalar. Esto dará como resultado un nuevo vector con la misma dirección pero producto de las dos magnitudes.

    Ejemplo\(\PageIndex{1}\):

    Por ejemplo, si tienes un vector A con cierta magnitud y dirección, multiplicarlo por un escalar a con magnitud 0.5 dará un nuevo vector con una magnitud de la mitad del original. Del mismo modo si tomas el número 3 que es un escalar puro y sin unidades y lo multiplica a un vector, obtienes una versión del vector original que es 3 veces más larga. Como ejemplo más físico tomemos la fuerza gravitacional sobre un objeto. La fuerza es un vector con su magnitud dependiendo del escalar conocido como masa y su dirección hacia abajo. Si se duplica la masa del objeto, también se duplica la fuerza de gravedad.

    Multiplicar vectores por escalares es muy útil en física. La mayoría de las unidades utilizadas en cantidades vectoriales son intrínsecamente escalares multiplicadas por el vector. Por ejemplo, la unidad de metros por segundo utilizada en velocidad, que es un vector, está compuesta por dos escalares, que son magnitudes: el escalar de longitud en metros y el escalar de tiempo en segundos. Para hacer esta conversión de magnitudes a velocidad, se debe multiplicar el vector unitario en una dirección particular por estos escalares.

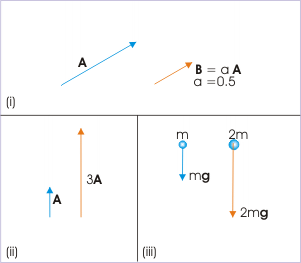
    imagen

    Multiplicación escalar: (i) Multiplicar el vector\(\mathrm{A}\) por el escalar\(\mathrm{a=0.5}\) produce el vector\(\mathrm{B}\) que es la mitad de largo. (ii) Multiplicar el vector\(\mathrm{A}\) por 3 triplica su longitud. (iii) Duplicar la masa (escalar) duplica la fuerza (vector) de la gravedad.

    Vectores unitarios y multiplicación por un escalar

    Multiplicar un vector por un escalar es lo mismo que multiplicar su magnitud por un número.

    objetivos de aprendizaje

    • Predecir la influencia de multiplicar un vector por un escalar

    Además de sumar vectores, los vectores también se pueden multiplicar por constantes conocidas como escalares. Los escalares son distintos de los vectores en que están representados por una magnitud pero ninguna dirección. Los ejemplos de escalares incluyen la masa, la altura o el volumen de un objeto.

    imagen

    Multiplicación escalar: (i) Multiplicar el vector\(\mathrm{A}\) por el escalar\(\mathrm{a=0.5}\) produce el vector\(\mathrm{B}\) que es la mitad de largo. (ii) Multiplicar el vector\(\mathrm{A}\) por 3 triplica su longitud. (iii) Duplicar la masa (escalar) duplica la fuerza (vector) de la gravedad.

    Al multiplicar un vector por un escalar, la dirección del vector no cambia y la magnitud se multiplica por la magnitud del escalar. Esto da como resultado una nueva flecha vectorial apuntando en la misma dirección que la anterior pero con una longitud mayor o menor. También se puede lograr la multiplicación escalar mediante el uso de los componentes de un vector. Una vez que tengas los componentes del vector, multiplica cada uno de los componentes por el escalar para obtener los nuevos componentes y así el nuevo vector.

    Un concepto útil en el estudio de vectores y geometría es el concepto de vector unitario. Un vector unitario es un vector con una longitud o magnitud de uno. Los vectores unitarios son diferentes para diferentes coordenadas. En las coordenadas cartesianas las direcciones son x e y usualmente denotadas\(\mathrm{\hat{x}}\) y\(\mathrm{\hat{y}}\). Con el triángulo por encima de las letras referidas como “sombrero”. Los vectores unitarios en coordenadas cartesianas describen un círculo conocido como el “círculo unitario” que tiene el radio uno. Esto se puede ver tomando todos los vectores posibles de longitud uno en todos los ángulos posibles en este sistema de coordenadas y colocándolos en las coordenadas. Si tuvieras que trazar una línea alrededor conectando todas las cabezas de todos los vectores juntos, obtendrías un círculo de radio uno.

    Posición, Desplazamiento, Velocidad y Aceleración como Vectores

    La posición, el desplazamiento, la velocidad y la aceleración se pueden mostrar todos vectores ya que se definen en términos de una magnitud y una dirección.

    objetivos de aprendizaje

    • Examinar las aplicaciones de los vectores en el análisis de cantidades físicas

    Uso de Vectores

    Los vectores pueden ser utilizados para representar cantidades físicas. Más comúnmente en física, los vectores se utilizan para representar el desplazamiento, la velocidad y la aceleración. Los vectores son una combinación de magnitud y dirección, y se dibujan como flechas. La longitud representa la magnitud y la dirección de esa cantidad es la dirección en la que apunta el vector. Debido a que los vectores se construyen de esta manera, es útil analizar cantidades físicas (con tamaño y dirección) como vectores.

    Aplicaciones

    En física, los vectores son útiles porque pueden representar visualmente la posición, el desplazamiento, la velocidad y la aceleración. Al dibujar vectores, muchas veces no tienes suficiente espacio para dibujarlos a la escala que están representando, por lo que es importante denotar en algún lugar a qué escala se están dibujando. Por ejemplo, cuando se dibuja un vector que representa una magnitud de 100, se puede dibujar una línea de 5 unidades de largo a una escala de\(\frac{1}{20}\). Cuando la inversa de la escala se multiplica por la magnitud dibujada, debe ser igual a la magnitud real.

    Posición y Desplazamiento

    El desplazamiento se define como la distancia, en cualquier dirección, de un objeto en relación con la posición de otro objeto. Los físicos utilizan el concepto de vector de posición como herramienta gráfica para visualizar los desplazamientos. Un vector de posición expresa la posición de un objeto desde el origen de un sistema de coordenadas. Un vector de posición también se puede utilizar para mostrar la posición de un objeto en relación con un punto de referencia, objeto secundario o posición inicial (si se analiza qué tan lejos se ha movido el objeto de su ubicación original). El vector de posición es una línea recta dibujada desde el origen arbitrario hasta el objeto. Una vez dibujado, el vector tiene una longitud y una dirección relativas al sistema de coordenadas utilizado.

    Velocity

    La velocidad también se define en términos de magnitud y dirección. Para decir que algo está ganando o perdiendo velocidad también hay que decir cuánto y en qué dirección. Por ejemplo, un avión que vuela\(\mathrm{\frac{km}{h}}\) a 200 hacia el noreste puede ser representado por un vector que apunta en dirección noreste con una magnitud de 200\(\mathrm{\frac{km}{h}}\). Al dibujar el vector, la magnitud sólo es importante como una forma de comparar dos vectores de las mismas unidades. Entonces, si hubiera otro avión volando 100\(\mathrm{\frac{km}{h}}\) hacia el suroeste, la flecha vectorial debería ser la mitad de larga y apuntando en dirección al suroeste.

    Aceleración

    La aceleración, siendo la velocidad temporal de cambio de velocidad, se compone de una magnitud y una dirección, y se dibuja con el mismo concepto que un vector de velocidad. Un valor para la aceleración no sería útil en física si se desconociera la magnitud y dirección de esta aceleración, razón por la cual estos vectores son importantes. En un diagrama de cuerpo libre, por ejemplo, de un objeto que cae, sería útil utilizar un vector de aceleración cerca del objeto para denotar su aceleración hacia el suelo. Si la gravedad es la única fuerza que actúa sobre el objeto, este vector estaría apuntando hacia abajo con una magnitud de 9.81\(\mathrm{\frac{m}{s^2}}\) de 32.2\(\mathrm{\frac{ft}{s^2}}\).

    imagen

    Diagrama vectorial: Aquí hay un hombre caminando por una colina. Su dirección de desplazamiento está definida por el ángulo theta relativo al eje vertical y por la longitud de la flecha que sube la colina. También se le está acelerando a la baja por la gravedad.

    Puntos Clave

    • Los vectores se pueden dividir en dos componentes: magnitud y dirección.
    • Al tomar el vector a analizar como la hipotenusa, los componentes horizontal y vertical se pueden encontrar completando un triángulo rectángulo. El borde inferior del triángulo es el componente horizontal y el lado opuesto al ángulo es el componente vertical.
    • El ángulo que hace el vector con la horizontal se puede utilizar para calcular la longitud de los dos componentes.
    • Los escalares son cantidades físicas representadas por un solo número y sin dirección.
    • Los vectores son cantidades físicas que requieren tanto magnitud como dirección.
    • Los ejemplos de escalares incluyen altura, masa, área y volumen. Los ejemplos de vectores incluyen desplazamiento, velocidad y aceleración.
    • Para agregar vectores, coloque el primero sobre un conjunto de ejes con su cola en el origen. Coloca el siguiente vector con su cola en la cabeza del vector anterior. Cuando no haya más vectores, dibuje una línea recta desde el origen hasta la cabeza del último vector. Esta línea es la suma de los vectores.
    • Para restar vectores, proceda como si sumara los dos vectores, pero voltee el vector a restar a través de los ejes y luego unirlo cola a cabeza como si sumara.
    • Al sumar o restar cualquier número de vectores se obtiene un vector resultante.
    • Los vectores se pueden descomponer en componentes horizontales y verticales.
    • Una vez que los vectores se descomponen en componentes, se pueden agregar los componentes.
    • Al sumar los componentes respectivos de dos vectores se obtiene un vector que es la suma de los dos vectores.
    • Un vector es una cantidad con magnitud y dirección.
    • Un escalar es una cantidad con solo magnitud.
    • Multiplicar un vector por un escalar equivale a multiplicar la magnitud del vector por el escalar. El vector se alarga o encoge pero no cambia de dirección.
    • Un vector unitario es un vector de magnitud (longitud) 1.
    • Un escalar es una cantidad física que puede ser representada por un solo número. A diferencia de los vectores, los escalares no tienen dirección.
    • Multiplicar un vector por un escalar es lo mismo que multiplicar la magnitud del vector por el número representado por el escalar.
    • Los vectores son flechas que consisten en una magnitud y una dirección. Se utilizan en física para representar cantidades físicas que también tienen tanto magnitud como dirección.
    • Desplazamiento es un término físico que significa la distancia de un objeto a un punto de referencia. Dado que el desplazamiento contiene dos piezas de información: la distancia desde el punto de referencia y la dirección que se aleja del punto, está bien representado por un vector.
    • La velocidad se define como la tasa de cambio en el tiempo del desplazamiento. Para conocer la velocidad de un objeto se debe saber tanto qué tan rápido está cambiando el desplazamiento como en qué dirección. Por lo tanto, también está bien representado por un vector.
    • La aceleración, siendo la tasa de cambio de velocidad también requiere tanto una magnitud como una dirección relativa a algunas coordenadas.
    • Al dibujar vectores, muchas veces no tienes suficiente espacio para dibujarlos a la escala que están representando, por lo que es importante denotar en algún lugar a qué escala se están dibujando.

    Términos Clave

    • coordenadas: Números que indican una posición con respecto a algún eje. Ej:\(\mathrm{x}\) y\(\mathrm{y}\) las coordenadas indican la posición relativa a los ejes xx e yy.
    • axis: Una línea imaginaria alrededor de la cual un objeto gira o está dispuesto simétricamente.
    • magnitud: Un número asignado a un vector que indica su longitud.
    • Ejes de coordenadas: Un conjunto de líneas perpendiculares que definen coordenadas relativas a un origen. Ejemplo: los ejes de coordenadas x e y definen la posición horizontal y vertical.
    • origin: El centro de un eje de coordenadas, definido como la coordenada 0 en todos los ejes.
    • Componente: Una parte de un vector. Por ejemplo, componentes horizontales y verticales.
    • vector: Una cantidad dirigida, una con magnitud y dirección; la entre dos puntos.
    • magnitud: Un número asignado a un vector que indica su longitud.
    • escalar: Una cantidad que tiene magnitud pero no dirección; comparar vector.
    • vector unitario: Un vector de magnitud 1.
    • velocidad: La tasa de cambio de desplazamiento con respecto al cambio en el tiempo.
    • desplazamiento: La longitud y dirección de una línea recta entre dos objetos.
    • aceleración: la velocidad a la que cambia la velocidad de un cuerpo con el tiempo

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 3.2: Vectores is shared under a not declared license and was authored, remixed, and/or curated by Boundless.