12.1: Vectores en el Plano
- Page ID
- 116150
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describir un vector plano, usando la notación correcta.
- Realizar operaciones vectoriales básicas (multiplicación escalar, suma, resta).
- Expresar un vector en forma de componente.
- Explicar la fórmula para la magnitud de un vector.
- Expresar un vector en términos de vectores unitarios.
- Dar dos ejemplos de cantidades vectoriales.
Al describir el movimiento de un avión en vuelo, es importante comunicar dos datos: la dirección en la que viaja el avión y la velocidad del avión. Al medir una fuerza, como el empuje de los motores del avión, es importante describir no sólo la fuerza de esa fuerza, sino también la dirección en la que se aplica. Algunas cantidades, como o fuerza, se definen en términos tanto de tamaño (también llamado magnitud) como de dirección. Una cantidad que tiene magnitud y dirección se denomina vector. En los libros de texto, los vectores a menudo se denotan con letras en negritas, como\(\mathbf{v}\). Dado que es difícil escribir en negritas claras cuando escribimos vectores a mano, también incluiremos una flecha o arpón encima de la letra que representa al vector. Para que los vectores sean más claros en este libro de texto (y para reforzar la forma en que debes escribirlos a mano), generalmente usaremos flechas o arpones por encima de letras negritas (o cursivas) para representar vectores, dándonos\(\vec v\) o\(\vecs{v}\). Tenga en cuenta que algunas figuras seguirán usando solo letras en negritas para denotar vectores.
Un vector es una cantidad que tiene tanto magnitud como dirección.
Representación vectorial
Un vector en un plano está representado por un segmento de línea dirigido (una flecha). Los puntos finales del segmento se denominan punto inicial y punto terminal del vector. Una flecha desde el punto inicial hasta el punto terminal indica la dirección del vector. La longitud del segmento de línea representa su magnitud. Usamos la notación\(\|\vecs{v}\|\) para denotar la magnitud del vector\(\vecs{v}\). Un vector con un punto inicial y un punto terminal que son iguales se denomina vector cero, denotado\(\vecs{0}\). El vector cero es el único vector sin dirección, y por convención puede considerarse que tiene cualquier dirección conveniente para el problema en cuestión.
Los vectores con la misma magnitud y dirección se denominan vectores equivalentes. Tratamos a los vectores equivalentes como iguales, aunque tengan diferentes puntos iniciales. Así, si\(\vecs{v}\) y\(\vecs{w}\) son equivalentes, escribimos
\[\vecs{v}=\vecs{w}. \nonumber \]
Se dice que los vectores son vectores equivalentes si tienen la misma magnitud y dirección.
Las flechas en la Figura\(\PageIndex{1 (b)}\) son equivalentes. Cada flecha tiene la misma longitud y dirección. Un concepto estrechamente relacionado es la idea de vectores paralelos. Se dice que dos vectores son paralelos si tienen direcciones iguales u opuestas. Exploramos esta idea con más detalle más adelante en el capítulo. Un vector se define por su magnitud y dirección, independientemente de dónde se encuentre su punto inicial.
El uso de letras en negrita y minúsculas para nombrar vectores es una representación común en la impresión, pero hay notaciones alternativas. Al escribir el nombre de un vector a mano, por ejemplo, es más fácil bosquejar una flecha sobre la variable que mostrar que es un vector:\(\vec{v}\). Cuando un vector tiene punto inicial\(P\) y punto terminal\(Q\), la notación\(\vecd{PQ}\) es útil porque indica la dirección y ubicación del vector.
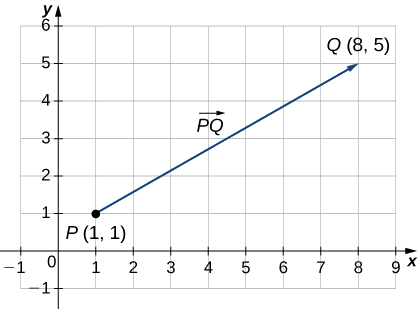
Realice el boceto de un vector en el plano desde el punto inicial\(P(1,1)\) hasta el punto terminal\(Q(8,5)\).
Solución
Ver Figura\(\PageIndex{2}\). Porque el vector va de punto\(P\) a punto\(Q\), lo nombramos\(\vecd{PQ}\).
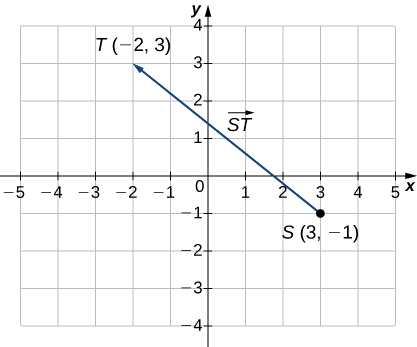
Esbozar el vector\(\vecd{ST}\) donde\(S\) es punto\((3,−1)\) y\(T\) es punto\((−2,3).\)
- Pista
-
El primer punto listado en el nombre del vector es el punto inicial del vector.
- Contestar
-
Combinando Vectores
Los vectores tienen muchas aplicaciones de la vida real, incluyendo situaciones que involucran fuerza o velocidad. Por ejemplo, consideremos las fuerzas que actúan en una embarcación que cruza un río. El motor de la embarcación genera una fuerza en una dirección, y la corriente del río genera una fuerza en otra dirección. Ambas fuerzas son vectores. Debemos tomar en cuenta tanto la magnitud como la dirección de cada fuerza si queremos saber a dónde irá la embarcación.
Un segundo ejemplo que involucra a vectores es un mariscal de campo lanzando un balón de fútbol. El mariscal de campo no lanza el balón paralelo al suelo; en cambio, apunta al aire. La velocidad de su lanzamiento puede ser representada por un vector. Si sabemos lo fuerte que lanza la pelota (magnitud—en este caso, la velocidad), y el ángulo (dirección), podemos decir hasta qué punto viajará la pelota por el campo.
Un número real a menudo se llama escalar en matemáticas y física. A diferencia de los vectores, generalmente se considera que los escalares tienen una magnitud solamente, pero ninguna dirección. Multiplicar un vector por un escalar cambia la magnitud del vector. Esto se llama multiplicación escalar. Tenga en cuenta que cambiar la magnitud de un vector no indica un cambio en su dirección. Por ejemplo, el viento que sopla de norte a sur podría aumentar o disminuir en velocidad manteniendo su dirección de norte a sur.
El producto\(k\vecs{v}\) de un vector\(\vecs{v}\) y un escalar\(k\) es un vector con una magnitud que es por\(|k|\) la magnitud de\(\vecs{v}\), y con una dirección que es la misma que la dirección de\(\vecs{v}\) si\(k>0\), y opuesta a la dirección de\(\vecs{v}\) si\(k<0\). A esto se le llama multiplicación escalar. Si\(k=0\) o\(\vecs{v}=\vecs{0}\), entonces\(k\vecs{v}=\vecs{0}.\)
Como es de esperar, si\(k=−1\), denotamos el producto\(k\vecs{v}\) como
\[k\vecs{v}=(−1)\vecs{v}=−\vecs{v}. \nonumber \]
Tenga en cuenta que\(−\vecs{v}\) tiene la misma magnitud que\(\vecs{v}\), pero tiene la dirección opuesta (Figura\(\PageIndex{3}\)).
Otra operación que podemos realizar en vectores es sumarlos juntos en adición de vectores, pero debido a que cada vector puede tener su propia dirección, el proceso es diferente de sumar dos números. El método gráfico más común para sumar dos vectores es colocar el punto inicial del segundo vector en el punto terminal del primero, como en la Figura\(\PageIndex{4 (a)}\). Para ver por qué esto tiene sentido, supongamos, por ejemplo, que ambos vectores representan desplazamiento. Si un objeto se mueve primero del punto inicial al punto terminal del vector\(\vecs{v}\), luego del punto inicial al punto terminal del vector\(\vecs{w}\), el desplazamiento general es el mismo que si el objeto hubiera realizado solo un movimiento desde el punto inicial hasta el punto terminal del vector \(\vecs{v}+\vecs{w}\). Por razones obvias, a este enfoque se le llama el método del triángulo. Observe que si hubiéramos cambiado el orden, así que ese\(\vecs{w}\) fue nuestro primer vector y\(\vecs{v}\) fue nuestro segundo vector, habríamos terminado en el mismo lugar. (Nuevamente, ver Figura\(\PageIndex{4 (a)}\).) Por lo tanto,
\[ \vecs{v}+ \vecs{w}= \vecs{w}+ \vecs{v}. \nonumber \]
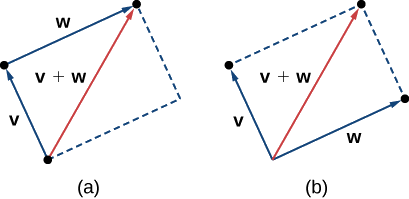
Un segundo método para agregar vectores se llama el método del paralelogramo. Con este método, colocamos los dos vectores para que tengan el mismo punto inicial, y luego dibujamos un paralelogramo con los vectores como dos lados adyacentes, como en la Figura\(\PageIndex{4 (b)}\). La longitud de la diagonal del paralelogramo es la suma. Comparando Figura\(\PageIndex{4 (b)}\) y Figura\(\PageIndex{4 (a)}\), podemos ver que obtenemos la misma respuesta usando cualquiera de los dos métodos. El vector\( \vecs{v}+ \vecs{w}\) se llama la suma del vector.
La suma de dos vectores\(\vecs{v}\) y se\(\vecs{w}\) puede construir gráficamente colocando el punto inicial de\(\vecs{w}\) en el punto terminal de\(\vecs{v}\). Entonces, el vector suma,\(\vecs{v}+\vecs{w}\), es el vector con un punto inicial que coincide con el punto inicial de\(\vecs{v}\) y tiene un punto terminal que coincide con el punto terminal de\(\vecs{w}\). Esta operación se conoce como adición de vectores.
También es apropiado aquí discutir la resta vectorial. Definimos\(\vecs{v}−\vecs{w}\) como\(\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\). El vector\(\vecs{v}−\vecs{w}\) se llama la diferencia de vector. Gráficamente, el vector\(\vecs{v}−\vecs{w}\) se representa dibujando un vector desde el punto terminal\(\vecs{w}\) hasta el punto terminal de\(\vecs{v}\) (Figura\(\PageIndex{5}\)).
En la Figura\(\PageIndex{4 (a)}\), el punto inicial de\(\vecs{v}+\vecs{w}\) es el punto inicial de\(\vecs{v}\). El punto terminal de\(\vecs{v}+\vecs{w}\) es el punto terminal de\(\vecs{w}\). Estos tres vectores forman los lados de un triángulo. De ello se deduce que la longitud de cualquier lado es menor que la suma de las longitudes de los lados restantes. Así que tenemos
\[\|\vecs{v}+\vecs{w}\|≤\|\vecs{v}\|+\|\vecs{w}\|. \nonumber \]
Esto se conoce de manera más general como la desigualdad triangular. Hay un caso, sin embargo, cuando el vector resultante\(\vecs{u}+\vecs{v}\) tiene la misma magnitud que la suma de las magnitudes de\(\vecs{u}\) y\(\vecs{v}\). Esto ocurre sólo cuando\(\vecs{u}\) y\(\vecs{v}\) tienen la misma dirección.
Dados los vectores\(\vecs{v}\) y\(\vecs{w}\) mostrados en la Figura\(\PageIndex{6}\), bosquejar los vectores
- \(3\vecs{w}\)
- \(\vecs{v}+\vecs{w}\)
- \(2\vecs{v}−\vecs{w}\)
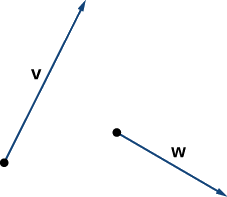
Solución
a. El vector\(3\vecs{w}\) tiene la misma dirección que\(\vecs{w}\); es tres veces más largo que\(\vecs{w}\).
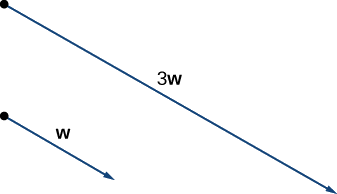
Vector\(3\vecs{w}\) tiene la misma dirección que\(\vecs{w}\) y es tres veces más largo.
b. Utilice cualquiera de los métodos de adición para encontrar\(\vecs{v}+\vecs{w}\).
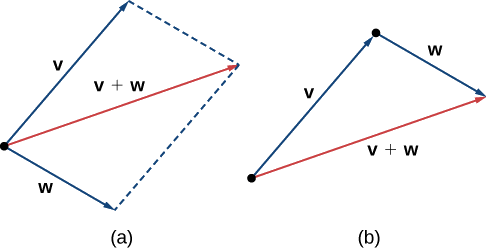
c. Para encontrar\(2\vecs{v}−\vecs{w}\), primero podemos reescribir la expresión como\(2\vecs{v}+(−\vecs{w})\). Entonces podemos dibujar el vector\(−\vecs{w}\), luego agregarlo al vector\(2\vecs{v}\).
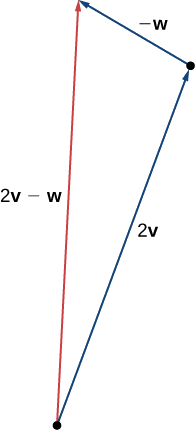
Usando vectores\(\vecs{v}\) y\(\vecs{w}\) a partir de Ejemplo\(\PageIndex{2}\), bosquejar el vector\(2\vecs{w}−\vecs{v}\).
- Pista
-
Primeros vectores de boceto\(2\vecs{w}\) y\(−\vecs{v}\).
- Contestar
-
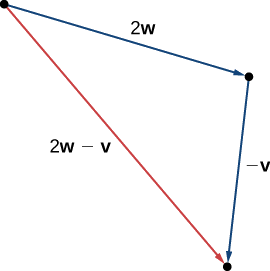
Componentes vectoriales
Trabajar con vectores en un plano es más fácil cuando estamos trabajando en un sistema de coordenadas. Cuando los puntos iniciales y los puntos terminales de los vectores se dan en coordenadas cartesianas, los cálculos se vuelven sencillos.
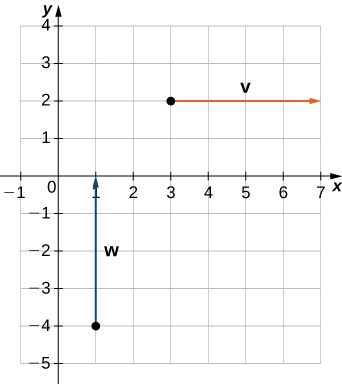
¿Son\(\vecs{v}\) vectores\(\vecs{w}\) equivalentes?
a.
- \(\vecs{v}\)tiene punto inicial\((3,2)\) y punto terminal\((7,2)\)
- \(\vecs{w}\)tiene punto inicial\((1,−4)\) y punto terminal\((1,0)\)
b.
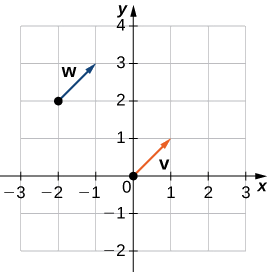
- \(\vecs{v}\)tiene punto inicial\((0,0)\) y punto terminal\((1,1)\)
- \(\vecs{w}\)tiene punto inicial\((−2,2)\) y punto terminal\((−1,3)\)
Solución
a. Cada uno de los vectores tiene una longitud de\(4\) unidades, pero están orientados en diferentes direcciones. Entonces\(\vecs{v}\) y no\(\vecs{w}\) son equivalentes (Figura\(\PageIndex{9}\)).
b. basado en la Figura\(\PageIndex{10}\), y usando un poco de geometría, es claro que estos vectores tienen la misma longitud y la misma dirección, por lo que\(\vecs{v}\) y\(\vecs{w}\) son equivalentes.
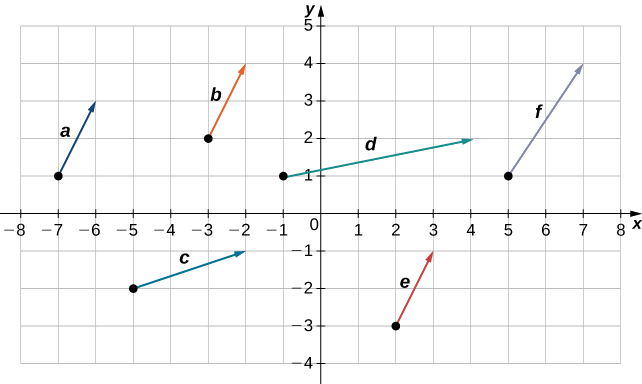
¿Cuáles de los siguientes vectores son equivalentes?
- Pista
-
Los vectores equivalentes tienen la misma magnitud y la misma dirección.
- Contestar
-
Vectores\(\vecs{a}, \vecs{b}\), y\(\vecs{e}\) son equivalentes.
Hemos visto cómo trazar un vector cuando se nos da un punto inicial y un punto terminal. Sin embargo, debido a que un vector se puede colocar en cualquier lugar de un plano, puede ser más fácil realizar cálculos con un vector cuando su punto inicial coincide con el origen. Llamamos a un vector con su punto inicial en el origen un vector de posición estándar. Debido a que se sabe que el punto inicial de cualquier vector en posición estándar es\((0,0)\), podemos describir el vector observando las coordenadas de su punto terminal. Así, si vector\(\vecs{v}\) tiene su punto inicial en el origen y su punto terminal en\((x,y),\) escribimos el vector en forma de componente como
\[\vecs{v}=⟨x,y⟩. \nonumber \]
Cuando un vector se escribe en forma de componente como esta, los escalares x e y se llaman los componentes de\(\vecs{v}\).
El vector con punto inicial\((0,0)\) y punto terminal se\((x,y)\) puede escribir en forma de componente como
\[\vecs{v}=⟨x,y⟩. \nonumber \]
Los escalares\(x\) y\(y\) se llaman los componentes de\(\vecs{v}\).
Recordemos que los vectores se nombran con letras minúsculas en negrita o dibujando una flecha sobre su nombre. También hemos aprendido que podemos nombrar un vector por su forma componente, con las coordenadas de su punto terminal entre corchetes angulares. Sin embargo, al escribir la forma componente de un vector, es importante distinguir entre\(⟨x,y⟩\) y\((x,y)\). El primer par ordenado utiliza corchetes angulares para describir un vector, mientras que el segundo usa paréntesis para describir un punto en un plano. El punto inicial de\(⟨x,y⟩\) es\((0,0)\); el punto terminal de\(⟨x,y⟩\) es\((x,y)\).
Cuando tenemos un vector que no está ya en posición estándar, podemos determinar su forma de componente de una de dos maneras. Podemos usar un enfoque geométrico, en el que esbozamos el vector en el plano de coordenadas, y luego bosquejamos un vector equivalente de posición estándar. Alternativamente, podemos encontrarlo algebraicamente, usando las coordenadas del punto inicial y el punto terminal. Para encontrarlo algebraicamente, restamos la\(x\) coordenada -del punto inicial de la\(x\) coordenada -del punto terminal para obtener el\(x\) -componente, y restamos la\(y\) coordenada -del punto inicial de la\(y\) coordenada -del punto terminal para obtener el\(y\) -componente.
Let\(\vecs{v}\) Ser un vector con punto inicial\((x_i,y_i)\) y punto terminal\((x_t,y_t)\). Entonces podemos expresarnos\(\vecs{v}\) en forma de componentes como\(\vecs{v}=⟨x_t−x_i,y_t−y_i⟩\).
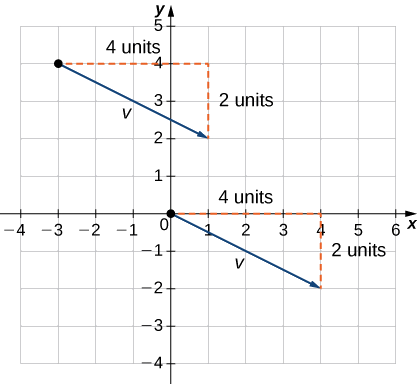
Vector expreso\(\vecs{v}\) con punto inicial\((−3,4)\) y punto terminal\((1,2)\) en forma de componente.
Solución:
a. Geométrico
1. Dibuja el vector en el plano de coordenadas (Figura\(\PageIndex{11}\)).
2. El punto terminal está a 4 unidades a la derecha y 2 unidades hacia abajo desde el punto inicial.
3. Encuentra el punto que está 4 unidades a la derecha y 2 unidades abajo del origen.
4. En posición estándar, este vector tiene punto inicial\((0,0)\) y punto terminal\((4,−2)\):
\(\vecs{v}=⟨4,−2⟩.\)
b. Algebraico
En la primera solución, se utilizó un boceto del vector para ver que el punto terminal se encuentra 4 unidades a la derecha. Podemos lograr esto algebraicamente encontrando la diferencia de las\(x\) coordenadas -:
\(x_t−x_i=1−(−3)=4.\)
De igual manera, la diferencia\(y\) de las coordenadas muestra la longitud vertical del vector.
\(y_t−y_i=2−4=−2.\)
Entonces, en forma de componentes,
\(\vecs{v}=⟨x_t−x_i,y_t−y_i⟩=⟨1−(−3),2−4⟩=⟨4,−2⟩.\)
Vector\(\vecs{w}\) tiene punto inicial\((−4,−5)\) y punto terminal\((−1,2)\). Expresar\(\vecs{w}\) en forma de componentes.
- Pista
-
Se puede utilizar el método geométrico o algebraico.
- Contestar
-
\(⟨3,7⟩\)
Para encontrar la magnitud de un vector, calculamos la distancia entre su punto inicial y su punto terminal. La magnitud del vector\(\vecs{v}=⟨x,y⟩\) se denota\(\|\vecs{v}\|,\) o\(|\vecs{v}|\), y se puede calcular usando la fórmula
\[\|\vecs{v}\|=\sqrt{x^2+y^2}. \nonumber \]
Obsérvese que debido a que este vector está escrito en forma de componente, es equivalente a un vector en posición estándar, con su punto inicial en el origen y punto terminal\((x,y)\). Así, basta con calcular la magnitud del vector en posición estándar. Usando la fórmula de distancia para calcular la distancia entre el punto inicial\((0,0)\) y el punto terminal\((x,y)\), tenemos
\[\|\vecs{v}\|=\sqrt{(x−0)^2+(y−0)^2}=\sqrt{x^2+y^2}. \nonumber \]
Con base en esta fórmula, es claro que para cualquier vector\(\vecs{v}, \|\vecs{v}\|≥0,\) y\(\|\vecs{v}\|=0\) si y sólo si\(\vecs{v}=\vecs{0}\).
La magnitud de un vector también se puede derivar utilizando el teorema de Pitágoras, como en la siguiente figura.
Hemos definido la multiplicación escalar y la adición vectorial geométricamente. Expresar vectores en forma de componentes nos permite realizar estas mismas operaciones algebraicamente.
Dejar\(\vecs{v}=⟨x_1,y_1⟩\) y\(\vecs{w}=⟨x_2,y_2⟩\) ser vectores, y dejar\(k\) ser un escalar.
- Multiplicación escalar:\[k\vecs{v}=⟨kx_1,ky_1⟩ \nonumber \]
- Adición de vectores:\[\vecs{v}+\vecs{w}=⟨x_1,y_1⟩+⟨x_2,y_2⟩=⟨x_1+x_2,y_1+y_2⟩ \nonumber \]
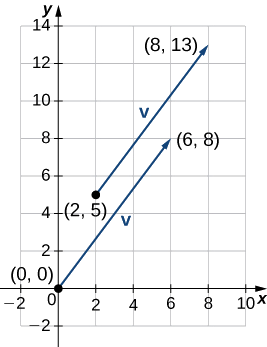
Dejar\(\vecs{v}\) ser el vector con punto inicial\((2,5)\) y punto terminal\((8,13)\), y let\(\vecs{w}=⟨−2,4⟩\).
- \(\vecs{v}\)Exprese en forma de componentes y encuentre\(\|\vecs{v}\|\). Luego, usando álgebra, encuentra
- \(\vecs{v}+\vecs{w}\),
- \(3\vecs{v}\), y
- \(\vecs{v}−2\vecs{w}\).
Solución
a. para colocar el punto inicial de\(\vecs{v}\) en el origen, debemos traducir el vector 2 unidades a la izquierda y 5 unidades hacia abajo (Figura\(\PageIndex{13}\)). Usando el método algebraico, podemos expresarnos\(\vecs{v}\) como\(\vecs{v}=⟨8−2,13−5⟩=⟨6,8⟩\):
\(\|\vecs{v}\|=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10\).
b. Para buscar\(\vecs{v}+\vecs{w}\), agregue los\(x\) -componentes y los\(y\) -componentes por separado:
\(\vecs{v}+\vecs{w}=⟨6,8⟩+⟨−2,4⟩=⟨4,12⟩.\)
c. Para encontrar\(3\vecs{v}\), multiplicar\(\vecs{v}\) por el escalar\(k=3\):
\(3\vecs{v}=3⋅⟨6,8⟩=⟨3⋅6,3⋅8⟩=⟨18,24⟩.\)
d. Para encontrarla\(\vecs{v}−2\vecs{w}\), encontrarla\(−2\vecs{w}\) y agregarla\(\vecs{v}:\)
\(\vecs{v}−2\vecs{w}=⟨6,8⟩−2⋅⟨−2,4⟩=⟨6,8⟩+⟨4,−8⟩=⟨10,0⟩.\)
Let\(\vecs{a}=⟨7,1⟩\) y let\(\vecs{b}\) ser el vector con punto inicial\((3,2)\) y punto terminal\((−1,−1).\)
- Encuentra\(\|\vecs{a}\|\).
- Expresar\(\vecs{b}\) en forma de componentes.
- Encuentra\(3\vecs{a}−4\vecs{b}.\)
- Pista
-
Usa el Teorema de Pitágoras para encontrar\(\|\vecs{a}\|\). Para encontrar\(3\vecs{a}−4\vecs{b}\), comience por encontrar los múltiplos escalares\(3\vecs{a}\) y\(−4\vecs{b}\).
- Contestar a
-
\(\|\vecs{a}\|=5\sqrt{2},\)
- Respuesta b
-
\(\vecs{b}=⟨−4,−3⟩,\)
- Respuesta c
-
\(3\vecs{a}−4\vecs{b}=⟨37,15⟩\)
Ahora que hemos establecido las reglas básicas de la aritmética vectorial, podemos declarar las propiedades de las operaciones vectoriales. Demostraremos dos de estas propiedades. Los otros pueden probarse de manera similar.
Dejar\(\vecs{u}, \, \vecs{v}\), y\(\vecs{w}\) ser vectores en un plano. Dejar\(r\) y\(s\) ser escalares.
- Propiedad conmutativa\[\vecs{u}+\vecs{v}=\vecs{v}+\vecs{u} \label{commutative} \]
- Propiedad asociativa\[(\vecs{u}+\vecs{v})+\vecs{w}=\vecs{u}+(\vecs{v}+\vecs{w}) \nonumber \]
- Propiedad de identidad aditiva\[\vecs{u}+\vecs{0}=\vecs{u} \nonumber \]
- Propiedad inversa aditiva\[\vecs{u}+(−\vecs{u})=\vecs{0} \nonumber \]
- Asociatividad de la multiplicación escalar\[r(s\vecs{u})=(rs)\vecs{u} \nonumber \]
- Propiedad distributiva\[(r+s)\vecs{u}=r\vecs{u}+s\vecs{u} \label{Distributive} \]
- Propiedad distributiva\[r(\vecs{u}+\vecs{v})=r\vecs{u}+r\vecs{v} \nonumber \]
- Identidad y cero propiedades\[1\vecs{u}=\vecs{u}, \, 0\vecs{u}=\vecs{0} \nonumber \]
Dejar\(\vecs{u}=⟨x_1,y_1⟩\) y\(\vecs{v}=⟨x_2,y_2⟩.\) aplicar la propiedad conmutativa para números reales:
\[ \begin{align*} \vecs{u}+\vecs{v} =⟨x_1+x_2,y_1+y_2⟩ \\[4pt] = ⟨x_2+x_1,y_2+y_1⟩ \\[4pt] = \vecs{v}+\vecs{u}. \end{align*}\]
□
Aplicar la propiedad distributiva para números reales:
\[ \begin{align*} r(\vecs{u}+\vecs{v}) =r⋅⟨x_1+x_2,y_1+y_2⟩ \\[4pt] =⟨r(x_1+x_2),r(y_1+y_2)⟩ \\[4pt] = ⟨rx_1+rx_2,ry_1+ry_2⟩ \\[4pt] = ⟨rx_1,ry_1⟩+⟨rx_2,ry_2⟩ \\[4pt] = r\vecs{u}+r\vecs{v}. \end{align*}\]
□
Demostrar la propiedad inversa aditiva.
- Pista
-
Utilice la forma componente de los vectores.
Hemos encontrado los componentes de un vector dados sus puntos inicial y terminal. En algunos casos, es posible que solo tengamos la magnitud y dirección de un vector, no los puntos. Para estos vectores, podemos identificar los componentes horizontal y vertical mediante trigonometría (Figura\(\PageIndex{14}\)).
Considera el ángulo\(θ\) formado por el vector\(\vecs{v}\) y el\(x\) eje positivo. Podemos ver desde el triángulo que\(\vecs{v}\) son los componentes del vector\(⟨\|\vecs{v}\| \cos{θ}, \, \|\vecs{v}\| \sin {θ}⟩\). Por lo tanto, dado un ángulo y la magnitud de un vector, podemos usar el coseno y el seno del ángulo para encontrar los componentes del vector.
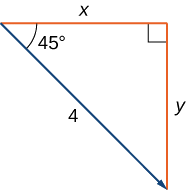
Encuentra la forma componente de un vector con magnitud 4 que forma un ángulo de\(−45°\) con el\(x\) eje.
Solución
Dejar\(x\) y\(y\) representar los componentes del vector (Figura\(\PageIndex{15}\)). Entonces\(x=4 \cos(−45°)=2 \sqrt{2}\) y\(y=4 \sin(−45°)=−2\sqrt{2}\). La forma componente del vector es\(⟨2\sqrt{2},−2\sqrt{2}⟩\).
Encuentra la forma componente de vector\(\vecs{v}\) con magnitud 10 que forma un ángulo de\(120°\) con el eje positivo\(x\).
- Pista
-
\(x=\|\vecs{v}\| \cos θ\)y\(y=\|\vecs{v}\| \sin θ\)
- Contestar
-
\(\vecs v=⟨−5,5\sqrt{3}⟩\)
Vectores unitarios
Un vector unitario es un vector con magnitud\(1\). Para cualquier vector distinto de cero\(\vecs{v}\), podemos usar la multiplicación escalar para encontrar un vector unitario\(\vecs{u}\) que tenga la misma dirección que\(\vecs{v}\). Para ello, multiplicamos el vector por el recíproco de su magnitud:
\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|} \vecs{v}. \nonumber \]
Recordemos que cuando definimos la multiplicación escalar, lo notamos\(\|k\vecs{v}\| =|k|⋅\|\vecs{v}\| \). Para\(\vecs{u}=\dfrac{1}{\|\vecs{v}\| }\vecs{v}\), se deduce que\(\|\vecs{u}\| =\dfrac{1}{\|\vecs{v}\| }(\|\vecs{v}\| )=1\). Decimos que\(\vecs{u}\) es el vector unitario en la dirección de\(\vecs{v}\) (Figura\(\PageIndex{16}\)). El proceso de usar la multiplicación escalar para encontrar un vector unitario con una dirección dada se llama normalización.
Vamos\(\vecs{v}=⟨1,2⟩\).
- Encuentra un vector unitario con la misma dirección que\(\vecs{v}\).
- Encuentra un vector\(\vecs{w}\) con la misma dirección que\(\vecs{v}\) tal que\(\|\vecs{w}\|=7\).
Solución:
a. primero, encontrar la magnitud de\(\vecs{v}\), luego dividir los componentes de\(\vecs{v}\) por la magnitud:
\[\|\vecs{v}\|=\sqrt{1^2+2^2}=\sqrt{1+4}=\sqrt{5} \nonumber \]
\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\sqrt{5}}⟨1,2⟩=⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩ \nonumber. \nonumber \]
b. El vector\(\vecs{u}\) está en la misma dirección que\(\vecs{v}\) y\(\|\vecs{u}\|=1\). Utilice la multiplicación escalar para aumentar la longitud de\(\vecs{u}\) sin cambiar de dirección:
\[\vecs{w}=7\vecs{u}=7⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩=⟨\dfrac{7}{\sqrt{5}},\dfrac{14}{\sqrt{5}}⟩ \nonumber. \nonumber \]
Vamos\(\vecs{v}=⟨9,2⟩\). Encontrar un vector con magnitud\(5\) en la dirección opuesta como\(\vecs{v}\).
- Pista
-
Primero, encuentra un vector unitario en la misma dirección que\(\vecs{v}\).
- Contestar
-
\(⟨−\dfrac{45}{\sqrt{85}},−\dfrac{10}{\sqrt{85}}⟩\)
Hemos visto lo conveniente que puede ser escribir un vector en forma de componente. A veces, sin embargo, es más conveniente escribir un vector como una suma de un vector horizontal y un vector vertical. Para que esto sea más fácil, veamos los vectores unitarios estándar. Los vectores unitarios estándar son los vectores\(\hat{\mathbf i}=⟨1,0⟩\) y\(\hat{\mathbf j}=⟨0,1⟩\) (Figura\(\PageIndex{17}\)).
Al aplicar las propiedades de los vectores, es posible expresar cualquier vector en términos de\(\hat{\mathbf i}\) y\(\hat{\mathbf j}\) en lo que llamamos una combinación lineal:
\[\vecs{v}=⟨x,y⟩=⟨x,0⟩+⟨0,y⟩=x⟨1,0⟩+y⟨0,1⟩=x\hat{\mathbf i}+y\hat{\mathbf j}. \nonumber \]
Así,\(\vecs{v}\) es la suma de un vector horizontal con magnitud\(x\), y un vector vertical con magnitud\(y\), como en la Figura\(\PageIndex{18}\).
- Expresar el vector\(\vecs{w}=⟨3,−4⟩\) en términos de vectores unitarios estándar.
- Vector\(\vecs{u}\) es un vector unitario que forma un ángulo de\(60°\) con el\(x\) eje positivo. Utilice vectores unitarios estándar para describir\(\vecs{u}\).
Solución:
a. Resolver\(\vecs{w}\) vector en un vector con un\(y\) componente cero y un vector con un\(x\) componente cero:
\[\vecs{w}=⟨3,−4⟩=3 \hat{\mathbf i}−4 \hat{\mathbf j}. \nonumber \]
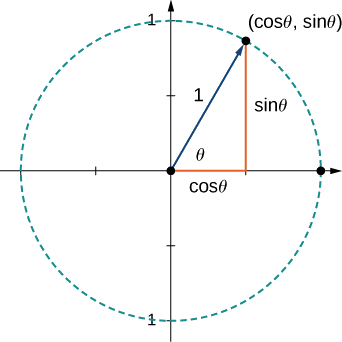
b. Debido a que\(\vecs{u}\) es un vector unitario, el punto terminal se encuentra en el círculo unitario cuando el vector se coloca en posición estándar (Figura\(\PageIndex{19}\)).
\[ \begin{align*} \vecs{u} =⟨\cos 60°,\sin 60°⟩ \\[4pt] =⟨\dfrac{1}{2},\dfrac{\sqrt{3}}{2}⟩ \\[4pt] = \dfrac{1}{2} \hat{\mathbf i}+\dfrac{\sqrt{3}}{2} \hat{\mathbf j}. \end{align*}\]
Let\(\vecs{a}=⟨16,−11⟩\) y let\(\vecs{b}\) ser un vector unitario que forma un ángulo de\(225°\) con el\(x\) eje positivo. Express\(\vecs{a}\) y\(\vecs{b}\) en términos de los vectores unitarios estándar.
- Pista
-
Use seno y coseno para encontrar los componentes de\(\vecs{b}\).
- Contestar
-
\(\vecs{a}=16 \hat{\mathbf i}−11 \hat{\mathbf j}, \quad \vecs{b}=−\dfrac{\sqrt{2}}{2} \hat{\mathbf i}−\dfrac{\sqrt{2}}{2} \hat{\mathbf j}\)
Aplicaciones de vectores
Debido a que los vectores tienen dirección y magnitud, son herramientas valiosas para resolver problemas que involucran aplicaciones como el movimiento y la fuerza. Recordemos el ejemplo de barco y el ejemplo de mariscal de campo que describimos anteriormente. Aquí nos fijamos en otros dos ejemplos en detalle.
El auto de Jane está atascado en el barro. Lisa y Jed vienen en una camioneta para ayudar a sacarla. Atan un extremo de una correa de remolque a la parte delantera del automóvil y el otro extremo al enganche del remolque del camión, y el camión comienza a tirar. En tanto, Jane y Jed se meten detrás del auto y empujan. El camión genera una fuerza horizontal de 300 lb en el auto. Jane y Jed están empujando en un ligero ángulo hacia arriba y generan una fuerza de 150 lb en el auto. Estas fuerzas pueden ser representadas por vectores, como se muestra en la Figura\(\PageIndex{20}\). El ángulo entre estos vectores es de 15°. Encuentra la fuerza resultante (la suma vectorial) y da su magnitud a la décima de libra más cercana y su ángulo de dirección desde el\(x\) eje positivo.
Solución
Para encontrar el efecto de combinar las dos fuerzas, agregue sus vectores representativos. Primero, expresar cada vector en forma de componente o en términos de los vectores unitarios estándar. Para ello, es más fácil si alineamos uno de los vectores con el\(x\) eje positivo. El vector horizontal, entonces, tiene punto inicial\((0,0)\) y punto terminal\((300,0)\). Se puede expresar como\(⟨300,0⟩\) o\(300 \hat{\mathbf i}\).
El segundo vector tiene magnitud\(150\) y hace un ángulo de\(15°\) con el primero, para que podamos expresarlo como\(⟨150 \cos(15°),150 \sin(15°)⟩,\) o\(150 \cos(15°)\hat{\mathbf i}+150 \sin(15°)\hat{\mathbf j}\). Entonces, la suma de los vectores, o vector resultante, es\(\vecs{r}=⟨300,0⟩+⟨150 \cos(15°),150 \sin(15°)⟩,\) y tenemos
\[\|\vecs{r}\|=\sqrt{(300+150 \cos(15°))^2+(150 \sin(15°))^2}≈446.6. \nonumber \]
El ángulo\(θ\) realizado por\(\vecs{r}\) y el\(x\) eje positivo tiene\(\tan θ=\dfrac{150 \sin 15°}{(300+150\cos 15°)}≈0.09\), entonces\(θ≈ \tan^{−1}(0.09)≈5°\), lo que significa que la fuerza resultante\(\vecs{r}\) tiene un ángulo\(5°\) por encima del eje horizontal.
Un avión vuela hacia el oeste a una velocidad aérea de\(425\) mph. El viento sopla del noreste a\(40\) mph. ¿Cuál es la velocidad de avance del avión? ¿Cuál es el rumbo del avión?
Solución
Empecemos por bosquejar la situación descrita (Figura\(\PageIndex{21}\)).
Configura un boceto para que los puntos iniciales de los vectores se encuentren en el origen. Entonces, el vector de velocidad del avión es\(\vecs{p}=−425\hat{\mathbf i}\). El vector que describe el viento forma un ángulo de\(225°\) con el\(x\) eje positivo:
\[\vecs{w}=⟨40 \cos(225°),40 \sin(225°)⟩=⟨−\dfrac{40}{\sqrt{2}},−\dfrac{40}{\sqrt{2}}⟩=−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]
Cuando la velocidad del aire y el viento actúan juntos en el avión, podemos sumar sus vectores para encontrar la fuerza resultante:
\[\vecs{p}+\vecs{w}=−425\hat{\mathbf i}+(−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j})=(−425−\dfrac{40}{\sqrt{2}})\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]
La magnitud del vector resultante muestra el efecto del viento sobre la velocidad del suelo del avión:
\(\|\vecs{p}+\vecs{w}\|=\sqrt{(−425−\dfrac{40}{\sqrt{2}})^2+(−\dfrac{40}{\sqrt{2}})^2}≈454.17\)mph
Como resultado del viento, el avión viaja aproximadamente a\(454\) mph con relación al suelo.
Para determinar el rumbo del avión, queremos encontrar la dirección del vector\(\vecs{p}+\vecs{w}\):
\(\tan θ=\dfrac{−\dfrac{40}{\sqrt{2}}}{(−425−\dfrac{40}{\sqrt{2}})}≈0.06\)
\(θ≈3.57°\).
La dirección general del avión es\(3.57°\) al sur de poniente.
Un avión vuela hacia el norte a una velocidad aérea de\(550\) mph. El viento sopla del noroeste a\(50\) mph. ¿Cuál es la velocidad de avance del avión?
- Pista
-
Dibuja los vectores con el mismo punto inicial y encuentra su suma.
- Contestar
-
Aproximadamente\(516\) mph
Conceptos clave
- Los vectores se utilizan para representar cantidades que tienen tanto magnitud como dirección.
- Podemos agregar vectores usando el método del paralelogramo o el método del triángulo para encontrar la suma. Podemos multiplicar un vector por un escalar para cambiar su longitud o darle la dirección opuesta.
- La resta de vectores se define en términos de sumar el negativo del vector.
- Un vector se escribe en forma de componente como\(\vecs{v}=⟨x,y⟩\).
- La magnitud de un vector es un escalar:\(‖\vecs{v}‖=\sqrt{x^2+y^2}\).
- Un vector unitario\(\vecs{u}\) tiene magnitud\(1\) y se puede encontrar dividiendo un vector por su magnitud:\(\vecs{u}=\dfrac{1}{‖\vecs{v}‖}\vecs{v}\). Los vectores unitarios estándar son\(\hat{\mathbf i}=⟨1,0⟩\) y\(\hat{\mathbf j}=⟨0,1⟩\). Un vector se\(\vecs{v}=⟨x,y⟩\) puede expresar en términos de los vectores unitarios estándar como\(\vecs{v}=x\hat{\mathbf i}+y\hat{\mathbf j}\).
- A menudo se utilizan vectores en física e ingeniería para representar fuerzas y velocidades, entre otras cantidades.
Glosario
- componente
- un escalar que describe la dirección vertical u horizontal de un vector
- vectores equivalentes
- vectores que tienen la misma magnitud y la misma dirección
- punto inicial
- el punto de partida de un vector
- magnitud
- la longitud de un vector
- normalización
- usando multiplicación escalar para encontrar un vector unitario con una dirección dada
- método de paralelogramo
- un método para encontrar la suma de dos vectores; posicionar los vectores para que compartan el mismo punto inicial; los vectores luego forman dos lados adyacentes de un paralelogramo; la suma de los vectores es la diagonal de ese paralelogramo
- escalar
- un número real
- multiplicación escalar
- una operación vectorial que define el producto de un escalar y un vector
- vector de posición estándar
- un vector con punto inicial\((0,0)\)
- vectores de unidad estándar
- vectores de unidad a lo largo de los ejes de coordenadas\(\hat{\mathbf i}=⟨1,0⟩,\, \hat{\mathbf j}=⟨0,1⟩\)
- punto terminal
- el punto final de un vector
- desigualdad triangular
- la longitud de cualquier lado de un triángulo es menor que la suma de las longitudes de los otros dos lados
- método triángulo
- un método para encontrar la suma de dos vectores; posicionar los vectores de manera que el punto terminal de un vector sea el punto inicial del otro; estos vectores luego forman dos lados de un triángulo; la suma de los vectores es el vector que forma el tercer lado; el punto inicial de la suma es el punto inicial del primero vector; el punto terminal de la suma es el punto terminal del segundo vector
- vector de unidad
- un vector con magnitud\(1\)
- vector
- un objeto matemático que tiene tanto magnitud como dirección
- adición de vectores
- una operación vectorial que define la suma de dos vectores
- diferencia vectorial
- la diferencia vectorial\(\vecs{v}−\vecs{w}\) se define como\(\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\)
- suma vectorial
- la suma de dos vectores,\(\vecs{v}\) y\(\vecs{w}\), se puede construir gráficamente colocando el punto inicial de\(\vecs{w}\) en el punto terminal de\(\vecs{v}\); entonces la suma vectorial\(\vecs{v}+\vecs{w}\) es el vector con un punto inicial que coincide con el punto inicial de\(\vecs{v}\), y con un punto terminal que coincide con el punto terminal de\(\vecs{w}\)
- vector cero
- el vector con punto inicial y punto terminal\((0,0)\)