Saltar al contenido principal
LibreTexts Español

3.3: Movimiento del proyectil

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128425
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Ecuaciones básicas y trayectoria parabólica

    El movimiento del proyectil es una forma de movimiento donde un objeto se mueve en trayectoria parabólica; la trayectoria que sigue el objeto se llama su trayectoria.

    objetivos de aprendizaje

    • Evaluar el efecto del ángulo y la velocidad en la trayectoria del proyectil; derivar la altura máxima mediante desplazamiento

    Movimiento de proyectiles

    El movimiento del proyectil es una forma de movimiento donde un objeto se mueve en una trayectoria parabólica bilateralmente simétrica. El camino que sigue el objeto se llama su trayectoria. El movimiento del proyectil solo ocurre cuando hay una fuerza aplicada al principio sobre la trayectoria, después de lo cual la única interferencia es de la gravedad. En un átomo anterior discutimos cuáles son los diversos componentes de un objeto en movimiento de proyectil. En este átomo discutiremos las ecuaciones básicas que las acompañan en el caso especial en el que las posiciones iniciales del proyectil son nulas (es decir,\(\mathrm{x_0=0}\) y\(\mathrm{y_0=0}\)).

    Velocidad Inicial

    La velocidad inicial se puede expresar como x componentes e y componentes:

    \[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ} \end{align}\]

    En esta ecuación,\(\mathrm{u}\) representa magnitud de velocidad inicial y\(θ\) se refiere al ángulo del proyectil.

    Tiempo de vuelo

    El tiempo de vuelo del movimiento de un proyectil es el tiempo desde que se proyecta el objeto hasta el momento en que alcanza la superficie. Como comentamos anteriormente,\(\mathrm{T}\) depende de la magnitud de la velocidad inicial y del ángulo del proyectil:

    \[\begin{align} \mathrm{T} & \mathrm{=\dfrac{2⋅u_y}{g} } \\ \mathrm{T} & \mathrm{=\dfrac{2⋅u⋅\sin ⁡θ}{g}} \end{align}\]

    Aceleración

    En el movimiento del proyectil, no hay aceleración en la dirección horizontal. La aceleración,\(\mathrm{a}\), en la dirección vertical se debe justamente a la gravedad, también conocida como caída libre:

    \[\begin{align} \mathrm{a_x} & \mathrm{=0} \\ \mathrm{a_y} &\mathrm{=−g} \end{align}\]

    Velocity

    La velocidad horizontal permanece constante, pero la velocidad vertical varía linealmente, debido a que la aceleración es constante. En cualquier momento,\(\mathrm{t}\), la velocidad es:

    \[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ−g⋅t} \end{align}\]

    También puedes usar el Teorema de Pitágoras para encontrar la velocidad:

    \[\mathrm{u=\sqrt{u_x^2+u_y^2}}\]

    Desplazamiento

    En el momento, t, los componentes de desplazamiento son:

    \[\begin{align} \mathrm{x} & \mathrm{=u⋅t⋅ \cos ⁡θ} \\ \mathrm{y} & \mathrm{=u⋅t⋅ \sin ⁡θ−\dfrac{1}{2}gt^2} \end{align}\]

    La ecuación para la magnitud del desplazamiento es\(\mathrm{Δr=\sqrt{x^2+y^2}}\).

    Trayectoria parabólica

    Podemos usar las ecuaciones de desplazamiento en la dirección x e y para obtener una ecuación para la forma parabólica del movimiento de un proyectil:

    \[\mathrm{y=\tan θ⋅x−\dfrac{g}{2⋅u^2⋅ \cos ^2 θ}⋅x^2}\]

    Altura Máxima

    La altura máxima se alcanza cuando\(\mathrm{v_y=0}\). Usando esto podemos reorganizar la ecuación de velocidad para encontrar el tiempo que tardará el objeto en alcanzar la altura máxima

    \[\mathrm{t_h=\dfrac{u⋅\sin θ}{g}}\]

    donde\(\mathrm{t_h}\) representa el tiempo que se tarda en alcanzar la altura máxima. A partir de la ecuación de desplazamiento podemos encontrar la altura máxima

    \[\mathrm{h=\dfrac{u^2⋅ \sin ^2 ⁡θ}{2⋅g}}\]

    Rango

    El rango del movimiento se fija por la condición\(\mathrm{y=0}\). Usando esto podemos reorganizar la ecuación de movimiento parabólico para encontrar el rango del movimiento:

    \[\mathrm{R=\dfrac{u^2⋅ \sin ⁡2 θ}{g}.}\]

    imagen

    Rango de Trayectoria: En esta figura se muestra el rango de una trayectoria.

    Proyectiles en Ángulo: Este video da una explicación clara y sencilla de cómo resolver un problema en Proyectiles Lanzados en Ángulo. Trato de ir paso a paso a través de este difícil problema de maquetar cómo resolverlo de una manera súper clara. Los problemas cinemáticos 2D tardan tiempo en resolverse, tomar notas sobre el orden de cómo lo resolví. Los mejores deseos. Sintonice mis otros videos para obtener más ayuda. Paz.

    Resolviendo problemas

    En el movimiento de proyectil, un objeto se mueve en trayectoria parabólica; la trayectoria que sigue el objeto se llama su trayectoria.

    objetivos de aprendizaje

    • Identificar qué componentes son esenciales para determinar el movimiento del proyectil de un objeto

    Anteriormente hemos discutido el movimiento del proyectil y sus componentes clave y ecuaciones básicas. Usando esa información, podemos resolver muchos problemas relacionados con el movimiento de proyectiles. Antes de hacer esto, revisemos algunos de los factores clave que entrarán en esta resolución de problemas.

    ¿Qué es el Movimiento de Proyectiles?

    El movimiento del proyectil es cuando un objeto se mueve en una trayectoria parabólica bilateralmente simétrica. El camino que sigue el objeto se llama su trayectoria. El movimiento del proyectil solo ocurre cuando hay una fuerza aplicada al inicio, después de lo cual la única influencia en la trayectoria es la de la gravedad.

    ¿Cuáles son los componentes clave del movimiento de proyectiles?

    Los componentes clave que debemos recordar para resolver problemas de movimiento de proyectiles son:

    • Ángulo de lanzamiento inicial,\(\mathrm{θ}\)
    • Velocidad inicial,\(\mathrm{u}\)
    • Tiempo de vuelo,\(\mathrm{T}\)
    • Aceleración,\(\mathrm{a}\)
    • Velocidad horizontal,\(\mathrm{v_x}\)
    • Velocidad vertical,\(\mathrm{v_y}\)
    • Desplazamiento,\(\mathrm{d}\)
    • Altura máxima,\(\mathrm{H}\)
    • Rango,\(\mathrm{R}\)

    Cómo resolver cualquier problema de movimiento de proyectiles (El método Toolbox): ¡Presentamos el método “Caja de herramientas” para resolver problemas de movimiento de proyectiles! Aquí utilizamos ecuaciones cinemáticas y modificamos con condiciones iniciales para generar una “caja de herramientas” de ecuaciones con las que resolver un problema clásico de movimiento de proyectiles de tres partes.

    Ahora, veamos dos ejemplos de problemas que involucran el movimiento de proyectiles.

    Ejemplo\(\PageIndex{1}\):

    Ejemplo 1

    Digamos que se le da un objeto que necesita despejar dos postes de igual altura separados por una distancia específica. Refiérase para este ejemplo. El proyectil se lanza a\(\mathrm{25 \sqrt{2}}\) m/s en un ángulo de 45°. Si el objeto es despejar ambos postes, cada uno con una altura de 30m, encontrar el mínimo: (a) posición del lanzamiento en el suelo en relación a los postes y (b) la separación entre los postes. Por simplicidad, use una constante de gravedad de 10. Problemas de cualquier tipo en física son mucho más fáciles de resolver si enumeras las cosas que sabes (los “dados”).

    imagen

    Diagrama para el Ejemplo 1: Utilice esta figura como referencia para resolver el ejemplo 1. El problema es asegurarse de que el objeto sea capaz de despejar ambos postes.

    Solución: Lo primero que tenemos que hacer es averiguar a qué hora tt el objeto alcanza la altura especificada. Dado que el movimiento está en forma parabólica, esto ocurrirá dos veces: una al viajar hacia arriba, y otra vez cuando el objeto se desplaza hacia abajo. Para ello podemos utilizar la ecuación de desplazamiento en la dirección vertical,\(\mathrm{y−y_0}\) :

    \[\mathrm{y−y_0=(v_y⋅t)−(\dfrac{1}{2}⋅g⋅t^2)}\]

    Sustituimos en las variables apropiadas:

    \[\mathrm{v_y=u⋅ \sin θ=25 \sqrt{2} \dfrac{m}{s}⋅ \sin 45^{\circ}=25 \dfrac{m}{s}}\]

    Por lo tanto:

    \[\mathrm{30m=25⋅t−\dfrac{1}{2}⋅10⋅t^2}\]

    Podemos usar la ecuación cuadrática para encontrar que las raíces de esta ecuación son 2s y 3s. Esto significa que el proyectil alcanzará 30m después de 2s, en su camino hacia arriba, y después de 3s, en su camino hacia abajo.

    Ejemplo 2

    Un objeto se lanza desde la base de una inclinación, que está en un ángulo de 30°. Si el ángulo de lanzamiento es de 60° con respecto a la horizontal y la velocidad de lanzamiento es de 10 m/s, ¿cuál es el tiempo total de vuelo? Se da la siguiente información:\(\mathrm{u=10 \frac{m}{s}; θ=60°; g=10 \frac{m}{s^2}}\).

    imagen

    Diagrama para el Ejemplo 2: Al tratar con un objeto en movimiento de proyectil sobre una inclinación, primero necesitamos usar la información dada para reorientar el sistema de coordenadas con el fin de que el objeto se lance y caiga sobre la misma superficie.

    Solución: Para dar cuenta del ángulo de inclinación, tenemos que reorientar el sistema de coordenadas para que los puntos de proyección y retorno estén en el mismo nivel. El ángulo de proyección con respecto a la\(\mathrm{x}\) dirección es\(\mathrm{θ−α}\), y la aceleración en la\(\mathrm{y}\) dirección es\(\mathrm{g⋅ \cos ⁡α}\). Reemplazamos\(\mathrm{θ}\) con\(\mathrm{θ−α}\) y\(\mathrm{g}\) con\(\mathrm{g⋅ \cos ⁡α}\):

    \[\begin{align} \mathrm{T \; } & \mathrm{=\dfrac{2⋅u⋅ \sin (θ)}{g} = \dfrac{2⋅u⋅\sin (θ−α)}{g⋅ \cos (α)}=\dfrac{2⋅10⋅ \sin (60−30)}{10⋅\cos (30)} =\dfrac{20⋅ \sin (30)}{10⋅ \cos (30)} } \\ \mathrm{T \;} &\mathrm{=\dfrac{2}{\sqrt{3}}s} \end{align}\]

    Ángulo de lanzamiento cero

    Un objeto lanzado horizontalmente a una altura\(\mathrm{H}\) recorre un rango\(\mathrm{v_0\sqrt{\frac{2H}{g}}}\) durante un tiempo de vuelo\(\mathrm{T=\sqrt{\frac{2H}{g}}}\).

    objetivos de aprendizaje

    • Explicar la relación entre el rango y el tiempo de vuelo

    El movimiento del proyectil es una forma de movimiento donde un objeto se mueve en una trayectoria parabólica. El camino seguido por el objeto se llama su trayectoria. El movimiento del proyectil ocurre cuando se aplica una fuerza al inicio de la trayectoria para el lanzamiento (después de esto el proyectil está sujeto solo a la gravedad).

    Uno de los componentes clave del movimiento del proyectil, y la trayectoria que sigue, es el ángulo de lanzamiento inicial. El ángulo en el que se lanza el objeto dicta el alcance, la altura y el tiempo de vuelo que experimentará el objeto mientras está en movimiento del proyectil. muestra diferentes caminos para el mismo objeto que se lanza a la misma velocidad inicial y diferentes ángulos de lanzamiento. Como lo ilustra la figura, cuanto mayor sea el ángulo de lanzamiento inicial y la altura máxima, mayor será el tiempo de vuelo del objeto.

    imagen

    Trayectorias de proyectiles: El ángulo de lanzamiento determina el alcance y la altura máxima que experimentará un objeto después de ser lanzado.Esta imagen muestra esa trayectoria del mismo objeto siendo lanzado a la misma velocidad pero diferentes ángulos.

    Anteriormente hemos discutido los efectos de diferentes ángulos de lanzamiento en el alcance, la altura y el tiempo de vuelo. Sin embargo, ¿qué pasa si no hay ángulo, y el objeto se acaba de lanzar horizontalmente? Tiene sentido que el objeto se lance a cierta altura (\(\mathrm{H}\)), de lo contrario no viajaría muy lejos antes de chocar contra el suelo. Examinemos cómo\(\mathrm{H}\) viaja un objeto lanzado horizontalmente a una altura. En nuestro caso es cuando\(\mathrm{α}\) es 0.

    imagen

    Movimiento del proyectil: Proyectil que se mueve siguiendo una parabola.El ángulo de lanzamiento inicial es αα, y la velocidad es\(\mathrm{v_0}\).

    Duración del vuelo

    No hay componente vertical en la velocidad inicial (\(\mathrm{v_0}\)) porque el objeto se lanza horizontalmente. Dado que el objeto recorre la distancia\(\mathrm{H}\) en dirección vertical antes de que golpee el suelo, podemos usar la ecuación cinemática para el movimiento vertical:

    \[\mathrm{(y−y_0)=−H=0⋅T−\dfrac{1}{2}gT^2}\]

    Aquí,\(\mathrm{T}\) es la duración del vuelo antes de que el objeto sea el suelo. Por lo tanto:

    \[\mathrm{T=\sqrt{\dfrac{2H}{g}}}\]

    Rango

    En la dirección horizontal, el objeto viaja a una velocidad constante\(\mathrm{v_0}\) durante el vuelo. Por lo tanto, el rango\(\mathrm{R}\) (en la dirección horizontal) se da como:

    \[\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\]

    Ángulo general de lanzamiento

    El ángulo de lanzamiento inicial (0-90 grados) de un objeto en movimiento de proyectil dicta el alcance, la altura y el tiempo de vuelo de ese objeto.

    objetivos de aprendizaje

    • Elija la ecuación adecuada para encontrar el rango, la altura máxima y el tiempo de vuelo

    El movimiento del proyectil es una forma de movimiento donde un objeto se mueve en una trayectoria parabólica bilateralmente simétrica. El camino que sigue el objeto se llama su trayectoria. El movimiento del proyectil solo ocurre cuando hay una fuerza aplicada al inicio de la trayectoria, después de lo cual la única interferencia es de la gravedad.

    Uno de los componentes clave del movimiento del proyectil y la trayectoria que sigue es el ángulo de lanzamiento inicial. Este ángulo puede ser de 0 a 90 grados. El ángulo en el que se lanza el objeto dicta el alcance, la altura y el tiempo de vuelo que experimentará mientras está en movimiento del proyectil. muestra diferentes caminos para el mismo objeto lanzado a la misma velocidad inicial en diferentes ángulos de lanzamiento. Como puede ver en la figura, cuanto mayor sea el ángulo de lanzamiento inicial, más cerca se acerca el objeto a la altura máxima y mayor será el tiempo de vuelo. El rango más grande se experimentará en un ángulo de lanzamiento de hasta 45 grados.

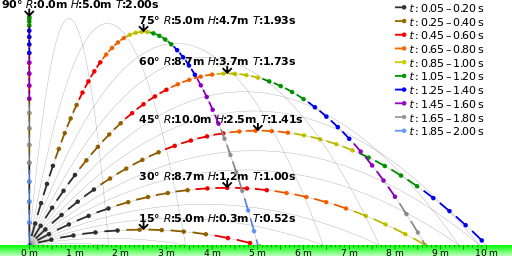
    imagen

    Ángulo de lanzamiento: El ángulo de lanzamiento determina el alcance y la altura máxima que experimentará un objeto después de ser lanzado. Esta imagen muestra esa trayectoria del mismo objeto siendo lanzado a la misma velocidad pero diferentes ángulos.

    El rango, la altura máxima y el tiempo de vuelo se pueden encontrar si conoce el ángulo de lanzamiento inicial y la velocidad, usando las siguientes ecuaciones:

    \[\begin{align} \mathrm{R \;} & \mathrm{=\dfrac{v_i^2 \sin ^⁡2 θ_i}{g}} \\ \mathrm{h \;} & \mathrm{=\dfrac{v_i^2 \sin ^2 ⁡θ_i}{2g}} \\ \mathrm{T \;} & \mathrm{=\dfrac{2v_i \sin θ}{g}} \end{align}\]

    Donde R — Rango, h — altura máxima, T — tiempo de vuelo, v i — velocidad inicial, θ i — ángulo de lanzamiento inicial, g — gravedad.

    Ahora que entendemos cómo el ángulo de lanzamiento juega un papel importante en muchos otros componentes de la trayectoria de un objeto en movimiento de proyectil, podemos aplicar ese conocimiento para hacer que un objeto aterrice donde lo queramos. Si hay cierta distancia, d, a la que quieres que vaya tu objeto y conoces la velocidad inicial a la que se lanzará, el ángulo de lanzamiento inicial requerido para obtenerlo esa distancia se llama el ángulo de alcance. Se puede encontrar usando la siguiente ecuación:

    \[\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\]

    Puntos Clave: Rango, Simetría, Altura Máxima

    El movimiento del proyectil es una forma de movimiento donde un objeto se mueve en trayectoria parabólica. El camino que sigue el objeto se llama su trayectoria.

    objetivos de aprendizaje

    • Construir un modelo de movimiento del proyectil incluyendo el tiempo de vuelo, la altura máxima y el alcance

    ¿Qué es el Movimiento de Proyectiles?

    El movimiento del proyectil es una forma de movimiento donde un objeto se mueve en una trayectoria parabólica bilateralmente simétrica. El camino que sigue el objeto se llama su trayectoria. El movimiento del proyectil solo ocurre cuando hay una fuerza aplicada al principio sobre la trayectoria, después de lo cual la única interferencia es de la gravedad. En este átomo vamos a discutir cuáles son los diversos componentes de un objeto en movimiento de proyectil, discutiremos las ecuaciones básicas que los acompañan en otro átomo, “Ecuaciones Básicas y Trayectoria Parabólica”

    Componentes clave del movimiento del proyectil:

    Tiempo de vuelo, T:

    El tiempo de vuelo de un movimiento de proyectil es exactamente lo que parece. Es el tiempo desde que se proyecta el objeto hasta el momento en que alcanza la superficie. El tiempo de vuelo depende de la velocidad inicial del objeto y del ángulo de la proyección, θθ. Cuando el punto de proyección y el punto de retorno están en el mismo plano horizontal, el desplazamiento vertical neto del objeto es cero.

    Simetría:

    Todo movimiento del proyectil ocurre en una trayectoria bilateralmente simétrica, siempre y cuando el punto de proyección y retorno ocurran a lo largo de la misma superficie horizontal. La simetría bilateral significa que el movimiento es simétrico en el plano vertical. Si tuvieras que trazar una línea vertical recta desde la altura máxima de la trayectoria, se reflejaría a lo largo de esta línea.

    Altura Máxima, H:

    La altura máxima de un objeto en una trayectoria de proyectil ocurre cuando la componente vertical de velocidad, vyvy, es igual a cero. A medida que el proyectil se mueve hacia arriba va contra la gravedad, y por lo tanto la velocidad comienza a desacelerarse. Eventualmente la velocidad vertical llegará a cero, y el proyectil se acelera hacia abajo bajo gravedad inmediatamente. Una vez que el proyectil alcanza su altura máxima, comienza a acelerar hacia abajo. Este es también el punto donde dibujarías una línea vertical de simetría.

    Alcance del Proyectil, R:

    El alcance del proyectil es el desplazamiento en la dirección horizontal. No hay aceleración en esta dirección ya que la gravedad sólo actúa verticalmente. muestra la línea de rango. Al igual que el tiempo de vuelo y la altura máxima, el alcance del proyectil es una función de la velocidad inicial.

    imagen

    Alcance: El alcance del movimiento de un proyectil, como se ve en esta imagen, es independiente de las fuerzas de gravedad.

    Puntos Clave

    • Los objetos que se proyectan desde, y aterrizan sobre la misma superficie horizontal, tendrán una trayectoria verticalmente simétrica.
    • El tiempo que tarda de un objeto en proyectarse y aterrizar se llama tiempo de vuelo. Esto depende de la velocidad inicial del proyectil y del ángulo de proyección.
    • Cuando el proyectil alcanza una velocidad vertical de cero, esta es la altura máxima del proyectil y luego la gravedad tomará el control y acelerará el objeto hacia abajo.
    • El desplazamiento horizontal del proyectil se denomina alcance del proyectil, y depende de la velocidad inicial del objeto.
    • A la hora de resolver problemas relacionados con el movimiento de proyectiles, debemos recordar todos los componentes clave del movimiento y las ecuaciones básicas que los acompañan.
    • Usando esa información, podemos resolver muchos tipos diferentes de problemas siempre y cuando podamos analizar la información que se nos da y usar las ecuaciones básicas para resolverla.
    • Para despejar dos postes de igual altura, y para averiguar cuál es la distancia entre estos postes, debemos recordar que la trayectoria es de forma parabólica y que hay dos momentos diferentes en los que el objeto alcanzará la altura de los postes.
    • Al tratar con un objeto en movimiento de proyectil sobre una inclinación, primero necesitamos usar la información dada para reorientar el sistema de coordenadas para que el objeto se lance y caiga sobre la misma superficie.
    • Para el ángulo de lanzamiento cero, no hay componente vertical en la velocidad inicial.
    • La duración del vuelo antes de que el objeto golpee el suelo se da como\(\mathrm{T=\sqrt{\frac{2H}{g}}}\).
    • En la dirección horizontal, el objeto viaja a una velocidad constante v 0 durante el vuelo. El rango R (en la dirección horizontal) se da como:\(\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\).
    • Si el mismo objeto es lanzado a la misma velocidad inicial, la altura y el tiempo de vuelo aumentarán proporcionalmente al ángulo de lanzamiento inicial.
    • Un objeto lanzado en movimiento de proyectil tendrá un ángulo de lanzamiento inicial en cualquier lugar de 0 a 90 grados.
    • El alcance de un objeto, dado el ángulo de lanzamiento inicial y la velocidad inicial se encuentra con:\(\mathrm{R=\dfrac{v_i^2 \sin ^⁡2 θ_i}{g}}\).
    • La altura máxima de un objeto, dado el ángulo de lanzamiento inicial y la velocidad inicial se encuentra con:\(\mathrm{ｈ=\dfrac{v_i^2 \sin ^2 ⁡θ_i}{2g}}\).
    • El tiempo de vuelo de un objeto, dado el ángulo de lanzamiento inicial y la velocidad inicial se encuentra con:\(\mathrm{T=\dfrac{2v_i \sin θ}{g}}\).
    • El ángulo de alcance es el ángulo al que se debe lanzar el objeto para lograr una distancia específica:\(\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\).
    • Los objetos que se proyectan desde y aterrizan sobre la misma superficie horizontal tendrán una trayectoria simétrica alrededor de una línea vertical a través de un punto a la altura máxima del proyectil.
    • El tiempo que tarda de un objeto en proyectarse y aterrizar se llama tiempo de vuelo. Depende de la velocidad inicial del proyectil y del ángulo de proyección.
    • La altura máxima del proyectil es cuando el proyectil alcanza una velocidad vertical cero. A partir de este punto la componente vertical del vector de velocidad apuntará hacia abajo.
    • El desplazamiento horizontal del proyectil se denomina alcance del proyectil y depende de la velocidad inicial del objeto.
    • Si un objeto se proyecta a la misma velocidad inicial, pero dos ángulos de proyección complementarios, el alcance del proyectil será el mismo.

    Términos Clave

    • trayectoria: El camino de un cuerpo a medida que viaja por el espacio.
    • simétrica: Presentar simetría; tener disposición armónica o proporcionada de las partes; tener partes o relaciones correspondientes.
    • reorientar: para orientar de nuevo; hacer que se enfrente a una dirección diferente
    • gravedad: Fuerza resultante en la superficie de la Tierra, de la atracción por las masas terrestres, y la pseudo-fuerza centrífuga causada por la rotación de la Tierra.
    • simetría bilateral: la propiedad de ser simétrico alrededor de un plano vertical

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 3.3: Movimiento del proyectil is shared under a not declared license and was authored, remixed, and/or curated by Boundless.