Saltar al contenido principal
LibreTexts Español

9.6: Conservación del Momentum Angular

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128519

    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    objetivos de aprendizaje

    • Evaluar las implicaciones del par neto en la conservación de energía

    Consideremos algunos ejemplos de impulso: la Tierra sigue girando al mismo ritmo que tiene desde hace miles de millones de años; un buzo alto que está “rotando” al saltar del tablero no necesita hacer ningún esfuerzo físico para seguir rotando, y de hecho sería incapaz de dejar de girar antes de golpear el agua. Estos ejemplos tienen las señas de identidad de una ley de conservación. A continuación se presentan otras observaciones a considerar:

    1. Se trata de un sistema cerrado. Nada es hacer un esfuerzo para torcer la Tierra o el buceador alto. Están aislados de influencias cambiantes de rotación (de ahí el término “sistema cerrado”).
    2. Algo permanece sin cambios. Parece haber una cantidad numérica para medir el movimiento rotacional tal que la cantidad total de esa cantidad permanece constante en un sistema cerrado.
    3. Algo se puede transferir de un lado a otro sin cambiar el monto total. Un buzo gira más rápido con los brazos y las piernas tirados hacia el pecho desde una postura completamente estirada.

    Momentum Angular

    La cantidad conservada que estamos investigando se llama momento angular. El símbolo para el momento angular es la letra L. Así como el momento lineal se conserva cuando no hay fuerzas externas netas, el momento angular es constante o se conserva cuando el par neto es cero. Podemos ver esto considerando la 2da ley de Newton para el movimiento rotacional:

    \(\mathrm{\overrightarrow{τ}=\frac{d \overrightarrow{L}}{dt}}\), donde\(\mathrm{τ}\) está el par. Para la situación en la que el par neto es cero,\(\mathrm{\frac{d \overrightarrow{L}}{dt}=0}\).

    Si el cambio en el momento angular ΔL es cero, entonces el momento angular es constante; por lo tanto,

    \(\mathrm{\overrightarrow{L}=constant}\)(cuando neta τ=0).

    Esta es una expresión para la ley de conservación del momento angular.

    Ejemplo e Implicaciones

    Un ejemplo de conservación del momento angular se ve en un patinador de hielo que ejecuta un giro, como se muestra en. El par neto sobre ella es muy cercano a cero, porque 1) hay relativamente poca fricción entre sus patines y el hielo, y 2) la fricción se ejerce muy cerca del punto de pivote.

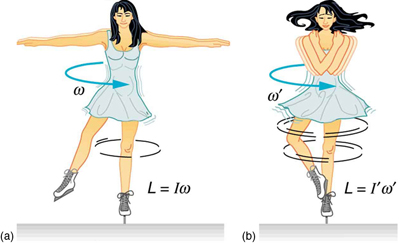
    imagen

    Conservación del Momentum Angular: Una patinadora sobre hielo gira sobre la punta de su patín con los brazos extendidos. Su momento angular se conserva porque el par neto sobre ella es insignificantemente pequeño. En la siguiente imagen, su ritmo de giro aumenta mucho cuando tira de sus brazos, disminuyendo su momento de inercia. El trabajo que realiza para tirar de sus brazos resulta en un aumento de la energía cinética rotacional.

    (Ambos\(F\) y\(r\) son pequeños, y así\(\mathrm{\overrightarrow{τ}=\overrightarrow{r} \times \overrightarrow{F} }\) es insignificantemente pequeños) En consecuencia, puede girar durante bastante tiempo. También puede aumentar su tasa de giro tirando de sus brazos y piernas. Cuando hace esto, la inercia rotacional disminuye y la velocidad de rotación aumenta para mantener\(\mathrm{L=Iω}\) constante el momento angular. (\(\mathrm{I}\): inercia rotacional,\(\mathrm{ω}\): velocidad angular)

    La conservación del momento angular es una de las leyes de conservación clave en la física, junto con las leyes de conservación para la energía y el impulso (lineal). Estas leyes son aplicables incluso en dominios microscópicos donde gobierna la mecánica cuántica; existen debido a las simetrías inherentes presentes en la naturaleza.

    Conservación de la Teoría del Momentum Angular: ¿Qué hace?

    Colisiones rotacionales

    En un sistema cerrado, el momento angular se conserva de manera similar al momento lineal.

    objetivos de aprendizaje

    • Evaluar la diferencia en las variables de ecuación en el momento rotacional versus angular

    Durante una colisión de objetos en un sistema cerrado, el impulso siempre se conserva. Este hecho se ve fácilmente en movimiento lineal. Cuando un objeto de masa m y velocidad v choca con otro objeto de masa m 2 y velocidad v 2, el impulso neto después de la colisión, mv 1f + mv 2f, es el mismo que el impulso antes de la colisión, mv 1i + mv 2i.

    ¿Qué pasa si se introduce un componente rotacional del movimiento? ¿Aún se conserva el impulso?

    imagen

    Bola de bolos y pi: Cuando una bola de boliche choca con un alfiler, se conserva el momento lineal y angular

    Sí. Para los objetos con un componente rotacional, existe un momento angular. El momento angular se define, matemáticamente, como\(\mathrm{L=Iω}\), o\(\mathrm{L=r \times p}\). Esta ecuación es un análogo a la definición de momento lineal como\(\mathrm{p=mv}\). Las unidades para el momento lineal son kgm/s mientras que las unidades para el momento angular son kgm 2 /s. Como era de esperar, un objeto que tiene un gran momento de inercia I, como la Tierra, tiene un momento angular muy grande. Un objeto que tiene una gran velocidad angular ω, como una centrífuga, también tiene un momento angular bastante grande.

    Así que los objetos rotativos que chocan en un sistema cerrado conservan no sólo el impulso lineal p en todas las direcciones, sino también el momento angular L en todas las direcciones.

    Por ejemplo, tomemos el caso de un arquero que decide disparar una flecha de masa m 1 a un cilindro estacionario de masa m 2 y radio r, acostado de costado. Si el arquero libera la flecha con una velocidad v 1i y la flecha golpea el cilindro en su borde radial, ¿cuál es el momento final?

    imagen

    Flecha golpeando la ciclina: La flecha golpea el borde del cilindro provocando que ruede.

    Inicialmente, el cilindro es estacionario, por lo que no tiene impulso lineal o radial. Una vez liberada la flecha, tiene un momento lineal\(\mathrm{p = m_{1i}}\) y una componente angular con relación al eje de rotación de los cilindros,\(\mathrm{L = rp = rm_1v_{1i}}\). Después de la colisión, la flecha se pega al cilindro rodante y el sistema tiene un momento angular neto igual al momento angular original de la flecha antes de la colisión.

    Puntos Clave

    • Cuando un objeto está girando en un sistema cerrado y no se le aplican pares externos, no tendrá ningún cambio en el momento angular.
    • La conservación del momento angular explica la aceleración angular de una patinadora sobre hielo a medida que acerca sus brazos y piernas al eje vertical de rotación.
    • Si el par neto es cero, entonces el momento angular es constante o conservado.
    • El momento angular se define, matemáticamente, como\(\mathrm{L=Iω}\), o\(\mathrm{L=r \times p}\). Que es el momento de inercia multiplicado por la velocidad angular, o el radio del objeto cruzado con el momento lineal.
    • En un sistema cerrado, el momento angular se conserva en todas las direcciones después de una colisión.
    • Dado que el impulso se conserva, parte del impulso en una colisión puede convertirse en un momento angular a medida que un objeto comienza a girar después de una colisión.

    Elementos clave

    • mecánica cuántica: La rama de la física que estudia la materia y la energía a nivel de átomos y otras partículas elementales; sustituye los mecanismos probabilísticos por los clásicos newtonianos.
    • par: Un efecto de rotación o torsión de una fuerza; (unidad SI newton-metro o Nm; unidad imperial pie-libra o ft-lb)
    • momento angular: Una cantidad vectorial que describe un objeto en movimiento circular; su magnitud es igual al momento de la partícula, y la dirección es perpendicular al plano de su movimiento circular.
    • momentum: (de un cuerpo en movimiento) producto de su masa y velocidad.
    • rotación: El acto de girar alrededor de un centro o de un eje.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 9.6: Conservación del Momentum Angular is shared under a not declared license and was authored, remixed, and/or curated by Boundless.