17A: La Ley Universal de la Gravitación

Considera un objeto liberado del reposo de un diámetro de luna entera por encima de la superficie de la luna. Supongamos que se le pide que calcule la velocidad con la que el objeto golpea la luna. Este problema tipifica el tipo de problema en el que los estudiantes utilizan la ley universal de la gravitación para obtener la fuerza ejercida sobre el objeto por el campo gravitacional de la luna, y luego usan erróneamente una o más de las ecuaciones de aceleración constante para obtener la velocidad final. El problema es: la aceleración no es constante. Cuanto más se acerca el objeto a la luna, mayor es la fuerza gravitacional, y por lo tanto, mayor es la aceleración del objeto. El error no radica en usar la segunda ley de Newton para determinar la aceleración del objeto en un punto particular del espacio; el error radica en usar ese único valor de aceleración, bueno para una distancia de objeto a luna, como si fuera válido en todo el camino del objeto. La manera de ir en un problema como este, es utilizar la conservación de la energía.

De vuelta en el capítulo 12, donde discutimos el campo gravitacional cercano a la superficie de la tierra, hablamos del hecho de que cualquier objeto que tenga masa crea un campo invisible fuerza por masa en la región del espacio a su alrededor. Lo llamamos campo gravitacional. Aquí hablamos de ello con más detalle. Recordemos que cuando decimos que un objeto hace que exista un campo gravitacional, queremos decir que crea un vector invisible fuerza por masa en cada punto de la región del espacio alrededor de sí mismo. El efecto del campo gravitacional sobre cualquier partícula (llamarla víctima) que se encuentre en la región del espacio donde existe el campo gravitacional, es ejercer una fuerza, sobre la víctima, igual al vector fuerza-por masa en la ubicación de la víctima, multiplicada por la masa de la víctima.

Ahora brindamos una discusión cuantitativa del campo gravitacional. (Medios cuantitativos, que involucran fórmulas, cálculos, y quizás números. Contraste esto con cualitativo que significa descriptivo/conceptual.) Partimos de la noción idealizada de partícula puntual de materia. Siendo materia, tiene masa. Al tener masa tiene un campo gravitacional en la región que lo rodea. La dirección del campo gravitacional de una partícula en el punto\(P\), a una\(r\) distancia de la partícula, es hacia la partícula y la magnitud del campo gravitacional viene dada por

\[g=G \frac{m}{r^2} \label{17-1}\]

donde:

\(G\)es la constante gravitacional universal:\(G=6.67 \times 10^{-11} \frac{N\cdot m^{2}}{kg^{2}}\)

\(m\)es la masa de la partícula, y:

\(r\)es la distancia que\(P\) está desde la partícula.

En ese punto\(P\) puede haber cualquier punto vacío (u ocupado) en el espacio cualquiera, esta fórmula da la magnitud del campo gravitacional de la partícula en todos los puntos del espacio. La ecuación\(\ref{17-1}\) es la forma de ecuación de la Ley Universal de Gravitación de Newton.

El vector de campo gravitacional total en un punto vacío en el espacio

Supongamos que tienes dos partículas. Cada uno tiene su propio campo gravitacional en todos los puntos del espacio. Consideremos un solo punto vacío en el espacio. Cada una de las dos partículas tiene su propio vector de campo gravitacional en ese punto vacío en el espacio. Podemos decir que cada partícula hace su propia contribución vectorial al campo gravitacional total en el punto vacío en el espacio en cuestión. Entonces, ¿cómo se determina el campo gravitacional total en el punto vacío en el espacio? ¡Lo adivinaste! Simplemente agregue las contribuciones individuales. Y debido a que la contribución debida a cada partícula es un vector, las dos contribuciones agregan como vectores.

Qué le hace el Campo Gravitacional a una Partícula que está en el Campo Gravitacional

Ahora supongamos que se tiene la magnitud y dirección del vector de campo gravitacional\(\vec{g}\) en un punto particular del espacio. El campo gravitacional ejerce una fuerza sobre cualquier partícula “víctima” que pasa a encontrarse en esa ubicación en el espacio. Supongamos, por ejemplo, que una partícula de masa se\(m\) encuentra en un punto del espacio donde está el campo gravitacional (de alguna otra partícula o partículas)\(\vec{g}\). Entonces la partícula de masa\(m\) está sujeta a una fuerza

\[\vec{F}_G=m \vec{g} \label{17-2}\]

El efecto gravitacional de una partícula sobre otra

Vamos a juntar las dos ideas precedentes. La partícula 1 de masa\(m_1\) tiene, entre su conjunto infinito de vectores de campo gravitacional, un vector de campo gravitacional en una ubicación\(r_{12}\) alejada de sí misma, un punto en el espacio que pasa a estar ocupado por otra partícula, la partícula 2, de masa\(m_2\). El campo gravitacional de la partícula 1 ejerce una fuerza sobre la partícula 2. La pregunta es, ¿qué tan grande y de qué manera es la fuerza?

Empecemos por identificar la ubicación de la partícula 2 como punto\(P\). \(P\)El punto está a una\(r_{12}\) distancia de la partícula 1. Así, la magnitud del vector de campo gravitacional (de la partícula 1) en el punto\(P\) es:

\[ g= G \frac{m_1}{r_{12}^2} \label{17-3}\]

Ahora la fuerza ejercida sobre la partícula 2 por el campo gravitacional de la partícula 1 viene dada por la ecuación\(\ref{17-2}\),\(\vec{F}_G=m_2\space\vec{g}\). Utilizando\(\vec{F}_{12}\) for\(\vec{F}_G\) para enfatizar el hecho de que estamos hablando de la fuerza de 1 sobre 2, y escribiendo la ecuación relacionando las magnitudes de los vectores que tenemos

\[F_{12}=m_2\space g\]

\(g\)Sustituyendo el por la expresión que acabamos de encontrar para la magnitud del campo gravitacional debido al número de partícula 1 que tenemos

\[F_{12}=m_2\space G\frac{m_1}{r_{12}^2}\]

que, con algún reordenamiento menor puede escribirse como

\[F_{12}=G \frac{m_1 \, m_2}{r_{12}^2} \label{17-4}\]

Esta ecuación da la fuerza del campo gravitacional de la partícula 1 sobre la partícula 2. Despreciando al “intermediario” (el campo gravitacional) podemos pensar en esto como la fuerza de la partícula 1 sobre la partícula 2. Se puede volver a pasar por todo el argumento, con los papeles de las partículas invertidos, para encontrar que la misma expresión se aplica a la fuerza de la partícula 2 sobre la partícula 1, o simplemente puede invocar la ^3ª Ley de Newton para llegar a la misma conclusión.

Objetos, en lugar de partículas puntuales

La suma vectorial de todos los vectores de campo gravitacional debido a una distribución esféricamente simétrica de partículas puntuales (por ejemplo, un objeto sólido esféricamente simétrico), en un punto fuera de la distribución (por ejemplo, fuera del objeto), es la misma que el vector de campo gravitacional debido a una sola partícula, en el centro de la distribución, cuya masa es igual a la suma de las masas de todas las partículas. También, para efectos de calcular la fuerza ejercida por el campo gravitacional de un objeto puntual sobre una víctima esféricamente simétrica, se puede tratar a la víctima como un objeto puntual en el centro de la víctima. Finalmente, respecto a cualquiera de los objetos en un cálculo de la fuerza gravitacional ejercida sobre un objeto rígido por el otro objeto: si la separación de los objetos es muy grande en comparación con las dimensiones del objeto, se puede tratar el objeto como una partícula puntual ubicada en el centro de masa del objeto y teniendo la misma masa que el objeto. Esto va para la energía potencial gravitacional, discutida a continuación, también.

¿Cómo Encaja esto con g= 9.80 N/kg?

Cuando hablamos antes del campo gravitacional cercano a la superficie de la tierra, usamos un solo valor para su magnitud, a saber, 9.80 N/kg y dijimos que siempre se dirigía hacia abajo, hacia el centro de la tierra. 9.80 N/kg es en realidad un valor promedio del nivel del mar. g varía dentro de aproximadamente medio por ciento de ese valor sobre la superficie de la tierra y el valor del manual incluye una pequeña contribución de campo de pseudo fuerza por masa centrífuga (que afecta tanto a la magnitud como a la dirección) derivada de la rotación de la tierra. Entonces, ¿cómo se relaciona el valor 9.80 N/kg para la magnitud del campo gravitacional cerca de la superficie de la tierra con la Ley Universal de Gravitación de Newton?

Ciertamente la dirección es consistente con nuestra comprensión de lo que debería ser: La tierra es más o menos esféricamente simétrica por lo que para fines de calcular el campo gravitacional fuera de la tierra podemos tratar a la tierra como una partícula puntual ubicada en el centro de la tierra. La dirección del campo gravitacional de una partícula puntual es hacia esa partícula puntual, por lo que, en cualquier lugar fuera de la tierra, incluso en cualquier punto justo fuera de la tierra (cerca de la superficie de la tierra), el campo gravitacional, de acuerdo con la Ley Universal de Gravitación, debe dirigirse hacia el centro de la tierra, una dirección que los terrícolas llamamos hacia abajo.

Pero, ¿qué tal la magnitud? ¿No debería variar con la elevación según la Ley Universal de la Gravitación? En primer lugar, ¿cómo se\(g=G\frac{m}{r^2}\) compara la magnitud calculada usando con 9.80 N/kg a, por ejemplo, el nivel del mar? Un punto al nivel del mar es una distancia\(r =6.37 \times10^6\) m del centro de la tierra. La masa de la tierra es\(\mbox{m} = 5.98\times10^{21} \mbox{kg}\). Sustituyendo estos valores en nuestra expresión por g (ecuación\(\ref{17-4}\) que dice\(g=G\frac{\mbox{m}}{r_{12}^2}\)) encontramos:

\[g=6.67\times 10^{-11} \frac{N\cdot m^2}{kg^2} \frac{5.98\times 10^{24} kg}{(6.37\times 10^6 m)^2}\]

\[g=9.83\frac{N}{kg}\]

que sí concuerda con el valor de 9.80 N/kg a dentro de aproximadamente 0.3 por ciento. (La diferencia se debe en parte al pseudo campo centrífugo de fuerza por masa asociado con la rotación de la tierra). En realidad podemos ver, solo por la forma en que se escribe el valor del radio de la tierra,\(6.37 \times10^6\) m, que aumentar nuestra elevación, incluso en una milla\(1.61\) km, no va a cambiar el valor de g a tres cifras significativas. Estaríamos aumentando r de\(6.37 \times10^6\) m a\(6.37161 \times10^6\) m que, a tres cifras significativas sigue siendo\(6.37 \times10^6\) m. Esto plantea la pregunta: “¿Qué tan alto por encima de la superficie hay que ir antes de que\(g=9.80\) N/kg ya no esté dentro de un cierto porcentaje del valor obtenido por medio de la Ley Universal de la Gravitación?” Investiguemos esa pregunta para el caso de una diferencia del 1 por ciento. Es decir, qué tan alto sobre el nivel del mar tendríamos que ir para hacer g = 99% de g a nivel del mar, es decir\(g=(.99)(9.80 m/s^2)=9.70 \) m/s ². Dejando\(r=r_E+h\) dónde\(r_E\) está el radio de la tierra, y usando g = 9.70 N/kg para que podamos encontrar la h que hace 9.70 N/kg tenemos:

\[g=\frac{Gm_E}{(r_E+h)^2}\]

Resolviendo esto para h rendimientos

\[h=\sqrt{\frac{Gm_E}{g}}-r_E\]

\[h=\sqrt{\frac{6.67\times10^{-11} \frac{N\cdot m^2}{kg^2} 5.98\times 10^{24} kg}{9.70 \frac{N}{kg}}}-6.37\times 10^6m \]

\[h=.04\times 10^6 m\]

Es decir que a cualquier altitud superior a 40 km sobre la superficie de la tierra, debes usar directamente la Ley Universal de Gravitación de Newton para que tus resultados sean buenos dentro del 1%.

En resumen, g=9.80 N/kg para la magnitud del campo gravitacional cercano a la superficie terrestre es una aproximación a la Ley Universal de Gravitación buena dentro de aproximadamente 1% en cualquier lugar dentro de aproximadamente 40 km de la superficie de la tierra. En esa región, el valor es aproximadamente una constante porque los cambios en la elevación representan una fracción tan pequeña de la distancia total de centro a superficie que es insignificante.

La energía potencial gravitacional universal

En lo que va de este curso se ha familiarizado con dos tipos de energía potencial, la energía potencial gravitacional cercana a la superficie de la tierra\(U_g=mgy\) y la energía potencial de primavera\(U_s=\frac{1}{2}kx^2\). Aquí presentamos otra expresión para la energía potencial gravitacional. Esta es pertinente a situaciones para las que es apropiada la Ley Universal de la Gravitación.

\[U_G=-\frac{G m_1\space m_2}{r_{12}} \label{17-5}\]

Esta es la energía potencial gravitacional de un par de partículas, una de masa m ₁ y la otra de masa m ₂, las cuales están separadas por una distancia de\(r_{12}\). Tenga en cuenta que para un par de partículas dado, la energía potencial gravitacional puede tomar valores desde el infinito negativo hasta cero. Cero es el valor más alto posible y es el valor de la energía potencial gravitacional en la separación infinita. Es decir eso\(U_G\xrightarrow{\lim r_{12}\to \infty} 0\). El valor más bajo concebible es el infinito negativo y sería el valor de la energía potencial gravitacional del par de partículas si se pudiera ponerlas tan juntas que ambas estuvieran en el mismo punto en el espacio. En notación matemática:\(U_G\xrightarrow {\lim r_{12}\to 0} -\infty\).

Conservación de problemas de energía mecánica que involucran energía potencial gravitacional universal para el caso especial en el que la cantidad total de energía mecánica no cambia

Resuelve cantidad fija de problemas de energía mecánica que involucran energía potencial gravitacional universal así como resolviste cantidad fija de problemas de energía mecánica que involucran otras formas de energía potencial allá por los capítulos 2 y 3. Dibuja una buena imagen de antes y después, escribe una ecuación que establezca que la energía en la imagen de antes es igual a la energía en la imagen posterior, y proceda de ahí. Para revisar estos procedimientos, consulte el problema de ejemplo en la página siguiente:

¿Qué tan grande tendría que ser la velocidad del hocico de un arma en la superficie de la luna para disparar una bala a una altitud de 101 km?

Solución: Necesitaremos los siguientes datos lunares:
Masa de la luna:\(m_m =7.35\times 10^{22} kg\); Radio de la luna:\(r_m =1.74\times 10^{6} m\);

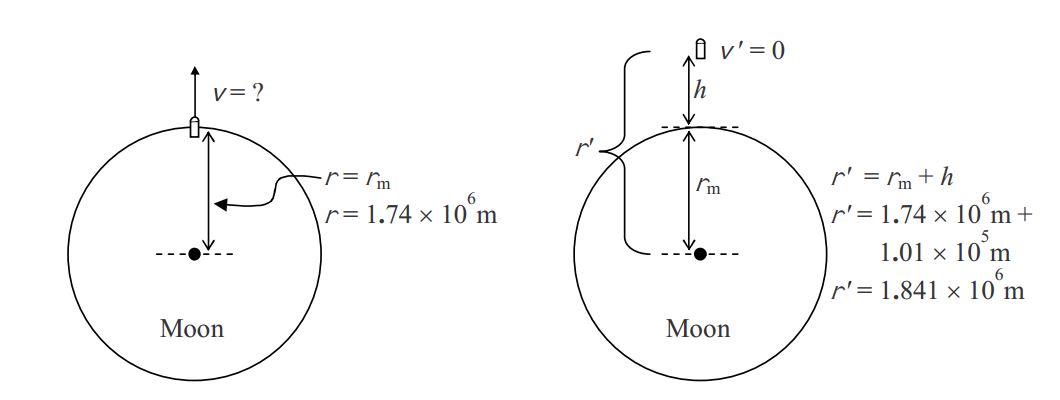
\[E=E'\]

\[K+U=K'+U'\]

\[\frac{1}{2}mv^2+-\frac{Gm_mm}{r}=-\frac{Gm_mm}{r'} \quad m_m \mbox{is the mass of the moon and m is the mass of the bullet.}\]

\[\frac{1}{2}v^2=\frac{G_m}{r}-\frac{G_m}{r'}\]

\[\frac{1}{2}v^2=G_m(\frac{1}{r}-\frac{1}{r'})\]

\[v=\sqrt{2Gm_m(\frac{1}{r}-\frac{1}{r'})}\]

\[v=\sqrt{2(6.67\times 10^{-11}\frac{N \cdot m^2}{kg^2})7.35\times 10^{22} kg (\frac{1}{1.74 \times 10^6 m}-\frac{1}{1.841\times 10^6 m})} \]

\[v=556\frac{m}{s}\]