6.6: Ejemplos

Ejemplo\(\PageIndex{1}\): Dejar caer un objeto en una báscula

(Versión corta) Supongamos que deja caer un objeto de 5 kg en una escala de resorte desde una altura de 1 m. Si la constante de resorte es\(k\) = 20, 000 N/m, ¿qué leerá la escala?

(Versión larga) Bien, vamos a romper eso en partes. Supongamos que una escala de resorte es solo una plataforma (de masa insignificante) sentada encima de un resorte. Si le pones un objeto de masa\(m\) encima, el resorte se comprime para que (en equilibrio) ejerza una fuerza ascendente que coincide con la de la gravedad.

1. Si la constante de resorte es\(k\) y la masa del objeto está\(m\) y todo el sistema está en reposo, ¿a qué distancia se comprime el resorte?
2. Si dejas caer el objeto desde una altura\(h\), ¿cuál es la compresión máxima (instantánea) del resorte a medida que el objeto se lleva a un descanso momentáneo? (¡Esta parte es un problema energético! Supongamos que\(h\) es mucho mayor que la compresión real del resorte, por lo que se puede descuidar eso al calcular el cambio en la energía potencial gravitacional.)
3. ¿Qué masa te daría esa misma compresión, si la colocaras suavemente en la balanza, y esperaras hasta que todas las oscilaciones se apagaran?
4. Bien, ¡ahora contesta la pregunta en la parte superior!

Solución

a) Las fuerzas que actúan sobre el objeto sentado en reposo sobre la plataforma son la fuerza de gravedad, \(F^G_{E,o} = −mg\), y la fuerza normal debida a la plataforma, \(F^n_{p,o}\). Esta última fuerza es igual, en magnitud, a la fuerza ejercida sobre la plataforma por el muelle (tiene que ser, porque la plataforma misma está siendo empujada hacia abajo por una fuerza\ (f^n_ {o, p} = −f^n_ {p, o}\), y ésta tiene que ser equilibrada por la fuerza del resorte). Esto significa que podemos, para fines prácticos, pretender que la plataforma no está ahí y simplemente establecer la fuerza hacia arriba sobre el objeto igual a la fuerza del resorte,\(F^{spr}_{s,p} = −k(x − x_0)\). Entonces, la segunda ley de Newton da

\ [F_ {n e t} =F_ {E, o} ^ {G} +F_ {s, p} ^ {s p r} =m a=0\ etiqueta {eq:6.33}.\]

Para un resorte comprimido,\ (x − x_0\) es negativo, y solo podemos dejar que\(d = x_0 − x\) sea la distancia que el resorte está comprimido. Entonces la ecuación (\ ref {eq:6.33}) da

\ [-m g+k d=0 \ nonumber\]

por lo

\[ d = mg/k \label{eq:6.34} \]

cuando solo pones un objeto en la escala y dejas que descanse.

b) Esta parte, como dice el problema, es una situación de conservación de la energía. El sistema formado por el resorte, el objeto y la tierra comienza con alguna energía potencial gravitacional, y termina, con el objeto momentáneamente en reposo, con solo energía potencial de resorte:

\ begin {align}
U_ {i} ^ {G} +U_ {i} ^ {s p r} &=U_ {f} ^ {G} +U_ {f} ^ {s p r}\ nonumber \\
m g y_ {i} +0 &=m g y_ {f} +\ frac {1} {2} k d_ {\ max} ^ {2} \ label {eq:6.35}
\ end {align}

donde he usado el subíndice “max” en la distancia de compresión para distinguirlo de lo que calculé en la parte (a) (este tipo de tiene sentido también porque la escala va a oscilar hacia arriba y hacia abajo, y queremos sólo la compresión máxima, lo que nos dará la lectura más grande). El problema decía ignorar la compresión a la hora de calcular el cambio en \(U^G\), es decir, que, si medimos la altura desde la parte superior de la escala,\(y_i = h\) y\(y_f = 0\). Entonces, resolviendo la Ecuación (\ ref {eq:6.35}) para\(d_{max}\), obtenemos

\ [d_ {\ max} =\ sqrt {\ frac {2 m g h} {k}}\ etiqueta {eq:6.36}.\]

(c) Para esta parte, vamos a reescribir la Ecuación (\ ref {eq:6.34}) como\(m_{eq} = kd_{max}/g\), donde\(m_{eq}\) está la masa “equivalente” que tendrías que colocar en la escala (suavemente) para obtener la misma lectura que en la parte (b). Usando entonces la ecuación (\ ref {eq:6.36}),

\ [m_ {e q} =\ frac {k} {g} \ sqrt {\ frac {2 m g h} {k}} =\ sqrt {\ frac {2 m k h} {g}}\ etiqueta {eq:6.37} .\]

(d) Ahora podemos sustituir los valores dados:\(m\) = 5 kg,\(h\) = 1 m,\(k\) = 20, 000 N/m El resultado es\(m_{eq}\) = 143 kg.

(Nota: si encontró confuso el tratamiento puramente algebraico anterior, intente sustituir valores numéricos en Eqs. (\ ref {eq:6.34}) y (\ ref {eq:6.36}). La primera ecuación te dice que si solo colocas la masa de 5 kg en la báscula se comprimirá una distancia\(d\) = 2.45 mm. El segundo te dice que si lo dejas caer comprimirá el resorte una distancia \(d_{max}\) = 70 mm, aproximadamente 28.6 veces más, lo que corresponde a una “masa equivalente” 28.6 veces mayor que 5 kg, es decir, 143 kg. Ten en cuenta también que 143 kg es un peso equivalente a 309 libras, así que si quieres probar esto en una báscula de baño te aconsejo que uses pesos más pequeños y los dejes caer desde una altura mucho menor!)

Ejemplo\(\PageIndex{2}\): Acelerar y ralentizar

1. Un automóvil de 1400 kg, partiendo del reposo, acelera a una velocidad de 30 mph en 10 s. ¿Cuál es la fuerza sobre el automóvil (supuesta constante) durante este periodo de tiempo?
2. ¿De dónde viene esta fuerza? Es decir, ¿cuál es el objeto (externo) que ejerce esta fuerza sobre el automóvil y cuál es la naturaleza de esta fuerza?
3. Dibuja un diagrama de cuerpo libre para el auto. Indicar la dirección del movimiento y la dirección de la aceleración.
4. Ahora suponga que el conductor, viajando a 30 mph, ve un semáforo rojo adelante y empuja el pedal del freno. Supongamos que el coeficiente de fricción estática entre las llantas y la carretera es \(\mu_s\) = 0.7, y que las ruedas no se “bloquean”: es decir, continúan rodando sin resbalar en la carretera mientras disminuyen la velocidad. ¿Cuál es la distancia mínima de parada del automóvil?
5. Dibuje un diagrama de carrocería libre del automóvil para la situación en (d). Nuevamente indicar la dirección del movimiento, y la dirección de la aceleración.
6. Ahora supongamos que el conductor nuevamente quiere detenerse como en la parte (c), pero presiona los frenos demasiado fuerte, por lo que las ruedas se bloquean, y, además, la carretera está mojada, y el coeficiente de fricción cinética es de sólo\(\mu_k\) = 0.2. ¿Cuál es la distancia que recorre el auto ahora antes de llegar a una parada?

Solución

(a) Primero, convertiremos 30 mph a metros por segundo. Hay 1.609 metros a una milla, y 3.600 segundos a una hora, por lo que 30 mph = 10 × 1609/3600 m/s = 13.4 m/s.

A continuación, para la aceleración constante, podemos usar la Ecuación (2.2.4): \(\Delta v = a \Delta t\). Resolviendo para\(a\),

\ [a=\ frac {\ Delta v} {\ Delta t} =\ frac {13.4\:\ mathrm {m}/\ mathrm {s}} {10\:\ mathrm {s}} =1.34\: \ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}}\ nonumber.\]

Por último, ya que\(F = ma\), tenemos

\ [f=m a=1400\:\ mathrm {kg} \ times 1.34\:\ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}} =1880\:\ mathrm {N} \ nonumber.\]

b) La fuerza debe ser proporcionada por la carretera, que es lo único externo al automóvil que esté en contacto con él. La fuerza es, de hecho, la fuerza de fricción estática entre el automóvil y las llantas. Como se explica en el capítulo, se trata de una fuerza de reacción (las llantas empujan en la carretera, y la carretera empuja hacia atrás). Es fricción estática porque las llantas no se deslizan con relación a la carretera. De hecho, veremos en el Capítulo 9 que el punto del neumático en contacto con la carretera tiene una velocidad instantánea de cero (ver Figura 9.6.1).

(c) Este es el diagrama de cuerpo libre. Observe la fuerza de fricción estática apuntando hacia adelante, en la dirección de la aceleración. Las fuerzas han sido dibujadas a escala.

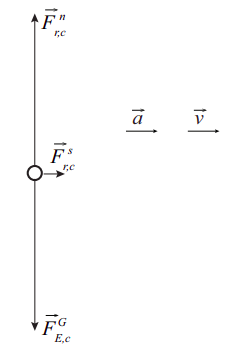
(d) Esto es lo opuesto a la parte (a): el conductor ahora confía en la fuerza de fricción estática para frenar el automóvil. La distancia de parada más corta corresponderá a la aceleración más grande (en magnitud), según nuestro viejo amigo, Ecuación (2.2.10):

\ [v_ {f} ^ {2} -v_ {i} ^ {2} =2 a\ Delta x\ etiqueta {eq:6.38}.\]

A su vez, la aceleración más grande corresponderá a la mayor fuerza. Como se explica en el capítulo, la fuerza de fricción estática no puede exceder\(\mu_sF^n\) (Ecuación (6.3.8)). Entonces, tenemos

\ [F_ {\ max} ^ {s} =\ mu_ {s} F^ {n} =\ mu_ {s} m g\ nonumber\]

ya que, en este caso, esperamos que la fuerza normal sea igual a la fuerza de gravedad. Entonces

\ [\ izquierda|a_ {\ max }\ derecha|=\ frac {F_ {\ max} ^ {s}} {m} =\ frac {\ mu_ {s} m g} {m} =\ mu_ {s} g \ nonumber.\]

Podemos sustituir esto en Ecuación (\ ref {eq:6.38}) por un signo negativo, ya que la aceleración actúa en dirección opuesta al movimiento (y estamos implícitamente tomando la dirección del movimiento para que sea positiva). También tenga en cuenta que la velocidad final que queremos es cero,\(v_f\) = 0. Obtenemos

\ [-v_ {i} ^ {2} =2 a\ Delta x=-2 \ mu_ {s} g\ Delta x\ nonumber.\]

A partir de aquí, podemos resolver para\ (\ Delta x\):

\ [\ Delta x=\ frac {v_ {i} ^ {2}} {2 \ mu_ {s} g} =\ frac {(13.4\:\ mathrm {m}/\ mathrm {s}) ^ {2}} {2\ times 0.7\ times 9.81\:\ mathrm {m}/\ mathrm {s} ^ {2}} =13.1\:\ mathrm {m} \ nonumber.\]

(e) Aquí está el diagrama de cuerpo libre. La característica interesante es que la fuerza de fricción estática ha invertido la dirección con respecto a las partes (a) — (c). También es mucho más grande que antes. (Las fuerzas están de nuevo a escala.)

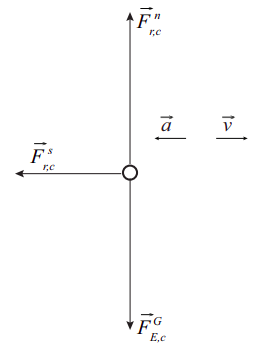
f) La matemática para esta parte es básicamente idéntica a la de la parte d). La diferencia, físicamente, es que ahora estás lidiando con la fuerza de la fricción cinética (o “deslizante”), y eso siempre viene dado por\(F^k = \mu_kF^n\) (esto no es un límite superior, es solo lo que\(F^k\) es). Así que tenemos \(a = −F^k/m = −mu_kg\), y, igual que antes (pero con\(\mu_k\) remplazamiento\(\mu_s\)),

\ [\ Delta x=\ frac {v_ {i} ^ {2}} {2 \ mu_ {k} g} =\ frac {(13.4\:\ mathrm {m}/\ mathrm {s}) ^ {2}} {2\ times 0.2\ times 9.81\:\ mathrm {m}/\ mathrm {s} ^ {2}} =45.8\:\ mathrm {m} \ nonumber.\]

Esta es una distancia enorme, ¡cerca de medio campo de fútbol! Si estos números son precisos, puedes ver que bloquear tus frenos bajo la lluvia puede tener algunas consecuencias bastante malas.