3.4: Movimiento relativo

Para describir el movimiento de un objeto confinado a una línea recta, se introdujo un eje (\(x\)) con una dirección especificada (en la que\(x\) aumenta) y un origen (dónde\(x=0\)). En ocasiones, puede ser más conveniente usar un eje que se esté moviendo. Por ejemplo, consideremos a una persona, Alice, moviéndose dentro de un tren que se dirigía a la ciudad francesa de Niza. El tren se mueve con una velocidad constante,\(v^{'B}\) medida desde el suelo. Supongamos que otra persona, Brice, describe la posición de Alice\(x^{A}(t)\) usando la función usando un\(x\) eje definido dentro del vagón del tren (\(x=0\)donde Brice está sentado, y positivo\(x\) está en la dirección del movimiento del tren), como se representa en la Figura\(\PageIndex{1}\) a continuación. Mientras cualquier persona esté en el tren con Brice, podrá describir fácilmente el movimiento de Alice usando el eje x que se mueve con el tren. Supongamos que el tren pasa por el pueblo francés de Hossegor, donde un surfista, Igor, vigila pasar el tren. Si Igor desea describir el movimiento de Alice, es más fácil para él usar un eje diferente, digamos\(x^{'}\), que esté fijado al suelo y que no se mueva con el tren.

Figura\(\PageIndex{1}\): Alicia camina en el tren y su poisición es descrita tanto por Brice, quien está sentada en la tran (usando el\(x\) eje), como Igor, quien está en reposo en el suelo (usando el\(x^{'}\) eje).

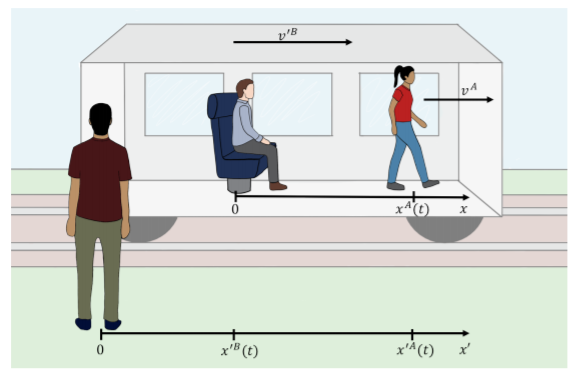
Dado que Brice ya pasó por el trabajo de determinar la función\(x^{A}(t)\) en el marco de referencia del tren, deseamos determinar cómo \(x^{A}(t)\)transformarse en el marco de referencia de la estación de tren,\(x^{'A}(t)\), para que Igor también pueda describir la moción de Alice. En otras palabras, queremos describir el movimiento de Alice en dos marcos de referencia diferentes.

Un marco de referencia es simplemente una elección de coordenadas, en este caso, una elección del eje x. Idealmente, en física, preferimos utilizar marcos de referencia inerciales, que son marcos de referencia que están “en reposo” o que se mueven a una velocidad constante en relación con un fotograma que consideramos en reposo.

En principio, si bloqueaste todas las ventanas del tren, no sería posible que Alice y Brice determinaran si el tren se mueve a velocidad constante o si está parado. Así, el concepto de “marco de descanso” es arbitrario en sí mismo. No es posible definir un marco de referencia que esté verdaderamente en reposo. Incluso el marco de referencia de Igor, la estación de tren, está en el planeta Tierra, que se mueve alrededor del Sol con una velocidad de\(108000\text{km/h}\).

Relatividad Galilea

No sólo es imposible definir un marco de referencia que esté verdaderamente en reposo, las reglas de la transformación de un fotograma a otro dependen de la velocidad entre los marcos de referencia. Nuestra experiencia común es descrita por lo que llamamos “Relatividad Galilea”, pero si la velocidad entre trenes es muy grande, cercana a la velocidad de la luz, entonces necesitamos usar la Teoría Especial de la Relatividad de Einstein.

Haciendo referencia a la Figura\(\PageIndex{1}\), deseamos utilizar la descripción de Brice del movimiento de Alice,\(x^{A}(t)\), y convertirla en una descripción,\(x^{'A}(t)\), que Igor puede usar en la estación de tren. Dado que Brice está en reposo en el tren, la velocidad de Brice relativa a Igor es\(v^{'B}(t)\) (la velocidad del tren, o la velocidad del\(x\) marco de referencia relativo al\(x^{'}\) marco de referencia). El primer paso es que Igor describa la posición de Brice,\(x^{'B}(t)\), (es decir, la posición del origen de Brice).

Supongamos que elegimos\(t = 0\) ser el punto en el tiempo donde se alinean los dos orígenes. Dado que el tren se mueve a una velocidad constante,\(v^{'B}\) (medida por Igor), entonces la posición del origen de Brice\(x^{'B}(t)\), medida desde el origen de Igor viene dada por:

\(x^{'B}(t)=v^{'B}t\)

Ahora que Igor puede describir la posición del origen del sistema de coordenadas de Brice, puede usar la descripción de Brice del movimiento de Alice. Recordemos que esa\(x^A(t)\) es la medida de Brice de la distancia de Alice con su origen. De igual manera\(x'^B(t)\),, es la medida de Igor de la distancia desde su origen hasta el origen de Brice. Así, para obtener la distancia de Alice del origen de Igor, simplemente agregamos la distancia,\(x'^B(t)\), desde el origen de Igor hasta el origen de Brice, y luego agregamos,\(x^A(t)\), la distancia desde el origen de Brice hasta Alice. Así:

\[x'^A(t)=x'^B(t)+x^A(t)=v'^Bt+x^A(t)\]

que nos dice cómo obtener la posición del objeto\(A\) en el marco de\(x^{'}\) referencia, cuando\(x^{A}(t)\) es la descripción la posición del objeto en el marco de\(x\) referencia que se mueve con una velocidad\(v^{'B}\) relativa a la \(x^{'}\)marco de referencia.

Como conocemos la posición de Alice medida en el marco de referencia de Igor, ahora podemos encontrar fácilmente su velocidad y su aceleración, medida por Igor. Su velocidad medida por Igor,\(v^{'A}\), viene dada por la derivada del tiempo de su posición medida en el marco de referencia de Igor:

\[\begin{aligned} v^{'A}(t)&=\frac{d}{dt}x^{'A}(t)\\ &=\frac{d}{dt}(v^{'B}t+x^{A}(t))\\ &=v^{'B}+\frac{d}{dt}x^{A}(t)\\ &=v^{'B}+v^{A}(t)\end{aligned}\]

donde\(v^A(t)=\frac{d}{dt}x^A(t)\) está la velocidad de Alice medida por Brice, en el tren. Es decir, la velocidad de Alice medida por Igor es la suma de la velocidad del tren en relación con el suelo y la velocidad de Alice en relación con el tren, lo cual tiene sentido. Si ahora determinamos la aceleración de Alice\(a'^A(t)\), medida por Igor, encontramos:

\[a^{'A}(t)=\frac{d}{dt}v^{'A}(t)\]

\[=\frac{d}{dt}(v^{'B}+v^{A})\]

\[=0+\frac{d}{dt}v^A(t)\]

\[=a^A\]

donde hemos utilizado explícitamente el hecho de que el tren se mueve a velocidad constante (\(\frac{d}{dt}v^{'B}=0\)). Aquí encontramos que tanto Brice como Igor medirán el mismo número al referirse a la aceleración de Alice (si el tren se mueve a velocidad constante). Esta es una particularidad del marco de referencia “inercial”: las aceleraciones no dependen del marco de referencia, siempre y cuando los marcos de referencia se muevan con una velocidad constante entre sí. Como veremos más adelante, las fuerzas ejercidas sobre un objeto están directamente relacionadas con la aceleración que experimenta ese objeto. Así, las fuerzas sobre un objeto no dependen de la elección del marco de referencia inercial.

Ejemplo\(\PageIndex{1}\)

Un barco grande navega hacia el norte a una velocidad de\(v^{'B}=15\text{m/s}\) and a restless passenger is walking about on the deck. Chloë, another passenger on the boat, finds that the passenger is walking at a constant speed of \(v^{A}=3\text{m/s}\) towards the South (opposite the direction of the boat’s motion). Marcel is watching the boat pass by from shore. What velocity (magnitude and direction) does Marcel measure for the restless passenger?

Solución:

Primero, debemos elegir sistemas de coordenadas en la embarcación y en la orilla. En la embarcación, definamos un\(x\) eje que sea positivo en dirección Norte y tenga un origen tal que la posición del pasajero inquieto estaba\(x^{A}(t=0)=0\) en su momento\(t=0\). En el marco de referencia de Chloë, el pasajero es así descrito por:

\[x^{A}(t)=v^{A}t=(-3\text{m/s})t\]

donde observamos que\(v^{A}\) es negativo ya que el pasajero está moviendo el en\(x\) dirección negativa (el pasajero está caminando hacia el Sur, pero elegimos positivo\(x\) para estar en dirección Norte). En tierra, elegimos un\(x^{'}\) eje que también sea positivo en dirección Norte. Podemos elegir el origen de tal manera que el origen del sistema de coordenadas de la embarcación fuera\(x^{'}=0\). El origen del sistema de coordenadas de la embarcación medido por Marcel (en tierra) es así:

\[x^{'B}(t)=v^{'B}t=(15\text{m/s})t\]

La posición del pasajero\(x^{'A}(t)\), medida por Marcel, se da luego sumando la posición del origen de la embarcación y la posición del pasajero medida desde el origen de la embarcación:

\[\begin{aligned} x^{'A}(t) &= x^{'B}(t)+x^{A}(t)\\ &= v^{'B}t + v^{A}t \\ &= (v^{'B}+v^{A})t\\ &= ((15\text{m/s})+(-3\text{m/s}))t\\ &= (12\text{m/s})t\end{aligned}\]

Para encontrar la velocidad del pasajero medida por Marcel, tomamos el tiempo derivado:

\[\begin{aligned} v^{'A} &= \frac{d}{dt}x^{'A}(t)\\ &= \frac{d}{dt} \left((v^{'B}+v^{A})t\right)\\ &=(v^{'B}+v^{A})\\ &=((15\text{m/s})+(-3\text{m/s}))\\ &=12\text{m/s}\end{aligned}\]

Al tratarse de un número positivo, Marcel sigue viendo al pasajero moviéndose en dirección Norte (la dirección de su\(x'\) eje positivo), pero con una velocidad de\(12\) m/s, que es menor que la de la embarcación. En la embarcación, el pasajero parece estar caminando hacia el Sur, pero el movimiento neto del pasajero relativo al suelo sigue en dirección Norte, ya que su velocidad es menor que la de la embarcación.