4.1: Movimiento en dos Dimensiones

Uso de vectores para describir el movimiento en dos dimensiones

Podemos especificar la ubicación de un objeto con sus coordenadas, y podemos describir cualquier desplazamiento por un vector. Primero, considere el caso de un objeto que se mueve con una velocidad constante en una dirección particular. Podemos especificar la posición del objeto en cualquier momento,\(t\), utilizando su vector de posición,\(\vec r(t)\), que es una función del tiempo. El vector de posición es un vector que va desde el origen del sistema de coordenadas hasta la posición del objeto. Podemos describir los\(y\) componentes\(x\) y del vector de posición con funciones independientes,\(x(t)\), y\(y(t)\), que corresponden a las\(y\) coordenadas\(x\) y del objeto en el momento \(t\), respectivamente:

\[\begin{aligned} \vec r(t) = \begin{pmatrix} x(t) \\ y(t) \\ \end{pmatrix}= x(t) \hat x + y(t) \hat y\end{aligned}\]

Supongamos que en un periodo de tiempo\(\Delta t\), el objeto pasa de una posición descrita por el vector de posición\(\vec r_1\) a una posición descrita por el vector de posición\(\vec r_2\), como se ilustra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Ilustración de un vector de desplazamiento\(∆\stackrel{\rightarrow}{r} = \stackrel{\rightarrow}{r_{2}}−\stackrel{\rightarrow}{r_{1}}\), para un objeto que se ubicó en posición\(\stackrel{\rightarrow}{r_{1}}\) en el tiempo\(t_{1}\) y en posición\(\stackrel{\rightarrow}{r_{2}}\) en el momento\(t_{2} = t_{1} + ∆t\).

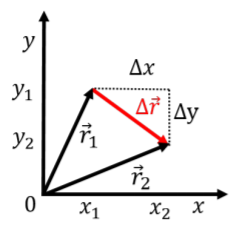
Podemos definir un vector de desplazamiento\(\Delta \vec r=\vec r_2-\vec r_1\), y por analogía al caso unidimensional, podemos definir un vector de velocidad promedio,\(\vec v\) como:

\[ \vec v = \frac{\Delta \vec r}{\Delta t}\]

El vector de velocidad promedio tendrá la misma dirección que\(\Delta \vec r\), ya que es el vector de desplazamiento dividido por un escalar (\(\Delta t\)). La magnitud del vector de velocidad, que llamamos “velocidad”, será proporcional a la longitud del vector de desplazamiento. Si el objeto se mueve una gran distancia en una pequeña cantidad de tiempo, tendrá así un vector de velocidad grande. Esta definición del vector de velocidad tiene así las propiedades intuitivas correctas (puntos en la dirección del movimiento, es más grande para objetos más rápidos).

Por ejemplo, si el objeto pasó de una posición\((x_1,y_1)\) a\((x_2,y_2)\) otra en una cantidad de tiempo\(\Delta t\), el vector de velocidad promedio viene dado por: Es\[\begin{aligned} \vec v &= \frac{\Delta \vec r}{\Delta t}\\ &=\frac{1}{\Delta t}\begin{pmatrix} x_2-x_1 \\ y_2-y_1 \\ \end{pmatrix}\\ &=\frac{1}{\Delta t}\begin{pmatrix} \Delta x \\ \Delta y \\ \end{pmatrix}\\ \end{aligned}\]\[\begin{aligned} &=\begin{pmatrix} \frac{\Delta x}{\Delta t} \\ \frac{\Delta y}{\Delta t}\\ \end{pmatrix}\\ &=\begin{pmatrix} v_x \\ v_y \\ \end{pmatrix}\\ \therefore \vec v &= v_x\hat x+v_y\hat y \end{aligned}\] decir, los\(y\) componentes\(x\) y del promedio vector de velocidad se puede encontrar determinando por separado la velocidad promedio en cada dirección. Por ejemplo,\(v_x=\frac{\Delta x}{\Delta t}\) corresponde a la velocidad promedio en la\(x\) dirección, y puede considerarse independiente de la velocidad en la\(y\) dirección,\(v_y\). La magnitud del vector de velocidad promedio (es decir, la velocidad promedio), viene dada por:\[\begin{aligned} ||\vec v||&=\sqrt{v_x^2+v_y^2}=\frac{1}{\Delta t}\sqrt{\Delta x^2+\Delta y^2}=\frac{\Delta r}{\Delta t}\end{aligned}\] donde\(\Delta r\) está la magnitud del vector de desplazamiento. Así, la velocidad promedio viene dada por la distancia recorrida dividida por el tiempo que se necesita para cubrir esa distancia, en analogía con el caso unidimensional.

Ejercicio\(\PageIndex{1}\)

Una llama corre en un campo desde una posición\((x_1,y_1)=(2\text{m},5\text{m})\) to a position \((x_2,y_2)=(6\text{m},8\text{m})\) in a time \(\Delta t=0.5\text{s}\), as measured by Marcel, a llama farmer standing at the origin of the Cartesian coordinate system. What is the average speed of the llama?

1. \(1\text{ m/s}\)
2. \(5\text{ m/s}\)
3. \(10\text{ m/s}\)
4. \(15\text{ m/s}\)

Responder

Si la velocidad del objeto no es constante, entonces definimos el vector de velocidad instantánea tomando el límite\(\Delta t\to 0\):

\[\vec v(t) = \lim_{\Delta t \to 0}\frac{\Delta \vec r}{\Delta t}=\frac{d\vec r}{dt}\]

lo que nos da la derivada del tiempo del vector de posición (en una dimensión, era la derivada del tiempo de la posición). Escribir los componentes del vector de posición como funciones\(x(t)\) y\(y(t)\), la velocidad instantánea se convierte en:

\[\stackrel{\rightarrow}{v}(t)=\frac{d}{dt}\stackrel{\rightarrow}{r}(t)\]

\[\begin{aligned} &=\frac{d}{dt} \begin{pmatrix} x(t) \\ y(t) \\ \end{pmatrix}\nonumber\\ &=\begin{pmatrix} \frac{dx}{dt} \\ \frac{dy}{dt} \\ \end{pmatrix}\nonumber\\ &=\begin{pmatrix} v_x(t) \\ v_y(t) \\ \end{pmatrix}\nonumber\\ \therefore \vec v(t) &= v_x(t)\hat x+v_y(t)\hat y \nonumber \end{aligned}\]

donde, nuevamente, encontramos que los componentes del vector de velocidad son simplemente las velocidades en la\(y\) dirección\(x\) y. Esto significa que podemos tratar el movimiento en dos dimensiones como un movimiento bidimensional: un movimiento a lo largo\(x\) y un movimiento separado a lo largo\(y\). Esto resalta la utilidad de la notación vectorial para permitirnos usar una ecuación vectorial (\(\vec v=\frac{d}{dt}\Delta \vec r\)) para representar dos ecuaciones (una para\(x\) y otra para\(y\)).

Del mismo modo, el vector de aceleración viene dado por:

\[\stackrel{\rightarrow}{a}(t)=\frac{d}{dt}\stackrel{\rightarrow}{v}(t) \]

\[\begin{aligned} &=\begin{pmatrix} \frac{dv_x}{dt} \\ \frac{dv_y}{dt} \\ \end{pmatrix}\nonumber\\ &=\begin{pmatrix} a_x(t) \\ a_y(t) \\ \end{pmatrix}\nonumber\\ \therefore \vec a(t) &= a_x(t)\hat x+a_y(t)\hat y \nonumber \end{aligned}\]

Si un objeto está en posición\(\vec r_0=(x_0,y_0)\) con un vector de velocidad\(\vec v_0=v_{0x}\hat x + v_{0y}\hat y\) a la vez\(t=0\), y tiene un vector de aceleración constante ^{1\(\vec a = a_x\hat x+a_y\hat y\)}, entonces el vector de velocidad en algún momento posterior\(t\), \(\vec v(t)\), viene dada por:

\[\begin{aligned} \vec v(t) = \vec v_0 + \vec a t\end{aligned}\]

O bien, si escribimos los componentes explícitamente:

\[\begin{aligned} \begin{pmatrix} v_x(t) \\ v_y(t) \\ \end{pmatrix} = \begin{pmatrix} v_{0x} \\ v_{0y} \\ \end{pmatrix} + \begin{pmatrix} a_xt \\ a_yt \\ \end{pmatrix}\end{aligned}\]

estas se consideran como dos ecuaciones independientes para los componentes del vector de velocidad:

\[\begin{aligned} v_x(t)&=v_{0x}+a_xt \\ v_y(t)&=v_{0y}+a_yt \\\end{aligned}\]

que es la misma ecuación que teníamos para la cinemática unidimensional, pero una vez por cada coordenada. El vector de posición viene dado por:

\[\begin{aligned} \vec r(t) = \vec r_0 + \vec v_0 t + \frac{1}{2} \vec at^2\end{aligned}\]

con componentes:

\[\begin{aligned} x(t) &= x_0+v_{0x}t+\frac{1}{2}a_xt^2\\ y(t) &= y_0+v_{0y}t+\frac{1}{2}a_yt^2\\\end{aligned}\]

lo que demuestra nuevamente que el movimiento bidimensional puede considerarse como movimientos separados e independientes en cada dirección.

Ejemplo\(\PageIndex{1}\)

Un objeto comienza en el origen de un sistema de coordenadas en el momento\(t=0\text{s}\), con un vector de velocidad inicial\(\vec v_0=(10\text{m/s})\hat x+(15\text{m/s})\hat y\). La aceleración en la\(x\) dirección es\(0\text{m/s}^{2}\) y la aceleración en la\(y\) dirección es\(-10\text{m/s}^{2}\).

1. Escribe una ecuación para el vector de posición en función del tiempo.
2. Determinar la posición del objeto en\(t = 10\text{s}\).
3. Trazar la trayectoria del objeto para el primero\(5\text{s}\) de movimiento.

Solución:

a. podemos considerar la moción en la\(y\) dirección\(x\) y por separado. En la\(x\) dirección, la aceleración es\(0\), y así la posición viene dada por:

\[\begin{aligned} x(t)&=x_0+v_{0x}t\\ &=(0\text{m})+(10\text{m/s})t\\ &=(10\text{m/s})t\end{aligned}\]

En la\(y\) dirección, tenemos una aceleración constante, por lo que la posición viene dada por:

\[\begin{aligned} y(t) &= y_0+v_{0y}t+\frac{1}{2}a_yt^2\\ &=(0\text{m})+(15\text{m/s})t+\frac{1}{2}(-10\text{m/s^2})t^2\\ &=(15\text{m/s})t-\frac{1}{2}(10\text{m/s^2})t^2\\\end{aligned}\]

El vector de posición en función del tiempo se puede escribir así como:

\[\begin{aligned} \vec r(t) &= \begin{pmatrix} x(t) \\ y(t) \\ \end{pmatrix}\\ &= \begin{pmatrix} (10\text{m/s})t \\ (15\text{m/s})t-\frac{1}{2}(10\text{m/s}^{2})t^{2} \\ \end{pmatrix}\end{aligned}\]

b. El uso\(t=10\text{s}\) en la ecuación anterior da:

\[\begin{aligned} \vec r(t=10\text{s})&= \begin{pmatrix} (10\text{m/s})(10\text{s}) \\ (15\text{m/s})(10\text{s})-\frac{1}{2}(10\text{m/s}^{2})(10\text{s})^{2} \\ \end{pmatrix}\\ &= \begin{pmatrix} (100\text{m}) \\ (-350\text{m})\\ \end{pmatrix}\end{aligned}\]

c. Podemos trazar la trayectoria usando python, como en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Trayectoria parabólica de un objeto sin aceleración en la\(x\) dirección y una aceleración negativa en la\(y\) dirección.

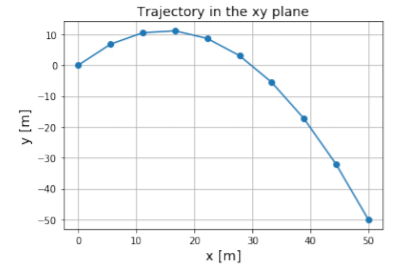
Como puedes ver, la trayectoria es una parábola, y corresponde a lo que obtendrías al lanzar un objeto con una velocidad inicial con componentes ascendentes (positivos\(y\)) y horizontales (positivos\(x\)). Si miras solo el\(y\) eje, verás que el objeto primero sube, luego da la vuelta y vuelve a bajar. Esto es exactamente lo que sucede cuando lanzas una pelota hacia arriba, independientemente de si el objeto se mueve en la\(x\) dirección. En la\(x\) dirección, el objeto simplemente se mueve con una velocidad constante. Los puntos en la gráfica se dibujan para intervalos de tiempo constantes (el tiempo entre cada punto,\(\Delta t\) es constante). Si miras la distancia entre puntos proyectados sobre el\(x\) eje, verás que todos son equidistantes y que a lo largo\(x\), el movimiento corresponde al de un objeto con velocidad constante.

Ejercicio\(\PageIndex{2}\)

En el Ejemplo 4.1.1, ¿cuál es el vector de velocidad exactamente en la parte superior de la parábola en la Figura\(\PageIndex{2}\)?

1. \(\stackrel{\rightarrow}{v} = (10\text{m/s})\stackrel{ˆ}{x}+(15\text{m/s})\stackrel{ˆ}{y}\)
2. \(\stackrel{\rightarrow}{v} = (15 m/s)\stackrel{ˆ}{y}\)
3. \(\stackrel{\rightarrow}{v} = (10 m/s)\stackrel{ˆ}{x}\)
4. Ninguna de las anteriores

Responder

Ejemplo\(\PageIndex{2}\)

Un mono está colgando de una rama de árbol y quieres darle de comer al mono tirándole un plátano (Figura\(\PageIndex{3}\)). Sabes que el mono se asusta fácilmente y soltará la rama del árbol en el instante en que tires el plátano. El mono está a una\(d\) distancia horizontal y una altura\(h\) por encima del punto desde el que sueltas el plátano cuando lo arrojas. ¿En qué ángulo con respecto a la horizontal debes tirar el plátano para que el plátano llegue al mono?

Figura\(\PageIndex{3}\): Alimentar a un mono en un árbol.

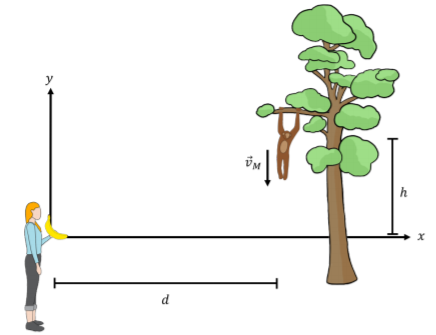
Solución:

Esta pregunta nos pide encontrar el ángulo,\(\theta\), entre el vector de velocidad inicial del plátano\(\vec v_{0B}\), y la horizontal para que el plátano golpee al mono. Este ángulo viene dado por los componentes horizontal (\(v_{B0x}\)) y vertical (\(v_{B0y}\)) del vector de velocidad inicial del plátano:

\[\begin{aligned} \tan\theta&=\frac{v_{B0y}}{v_{B0x}}\end{aligned}\]

Para que el plátano golpee al mono, y el plátano y el mono deben estar en el mismo lugar a la vez en algún momento,\(t\). Nuestro enfoque será el siguiente: comenzaremos por encontrar ecuaciones que describan la\(x\) y\(y\) posición del mono y del plátano. Entonces, usaremos nuestras condiciones para un “hit” exitoso para encontrar la proporción (\(\tan\theta=v_{B0y}/v_{B0x}\)) que queremos para nuestro lanzamiento inicial, y usaremos eso para encontrar\(\theta\).

Primero, definimos un sistema de coordenadas. Elegimos el origen para ser donde se libera el plátano. Dejamos\(y\) estar en la dirección vertical (positivo hacia arriba) y dejamos\(x\) estar en la dirección horizontal (positivo hacia el mono), como se muestra en la Figura\(\PageIndex{3}\).

Tratamos los\(y\) componentes\(x\) y de los vectores de velocidad y posición de banano y mono como independientes. El movimiento del mono solo tiene una componente vertical. El\(y\) componente de la aceleración del mono es la aceleración debida a la gravedad\(a_y=-9.8\text{m/s^2}= -g\), que es negativa, ya que la gravedad produce una aceleración en la\(y\) dirección negativa. El\(y\) componente de la posición inicial del mono es\(y_{M0}=h\) y el\(y\) componente de su velocidad inicial es\(v_{M0y}=0\). El\(y\) componente de la posición del mono en función del tiempo,\(y_M(t)\), viene dado por:

\[\begin{aligned} y_M(t)&=y_{M0}+v_{My0}t+\frac{1}{2}a_yt^2\\ &=h+(0)-\frac{1}{2}gt^2\end{aligned}\]

La posición horizontal del mono es constante, y es igual a\(x_M(t)=d\).

El movimiento del banano tiene ambos\(x\) y\(y\) componentes. No hay aceleración en la\(x\) dirección, por lo que el\(x\) componente de la velocidad del plátano es\(v_{B0x}\) y constante. Definimos que la\(x\) coordenada inicial del banano\(x_{B0}=0\) era, por lo que la\(x\) posición del banano en función del tiempo,\(x_B(t)\) viene dada por:

\[\begin{aligned} x_B(t)&=x_{B0}+v_{B0x}\\ &=(0)+v_{B0x}t\end{aligned}\]

Definimos la\(y\) posición inicial del plátano para ser\(y_{B0}=0\). La\(y\) posición del plátano en función del tiempo,\(y_B(t)\), puede ser descrita por:

\[\begin{aligned} y_B(t)&=y_{B0}+v_{B0y}t+\frac{1}{2}a_yt^2\\ &=(0)+v_{B0y}t-\frac{1}{2}gt^2\end{aligned}\]

donde\(v_{B0y}\) es el\(y\) componente de la velocidad inicial del plátano y\(a_y=-g\) es el\(y\) componente de la aceleración del plátano (debido a la gravedad). Ahora que tenemos ecuaciones que describen la posición tanto del plátano como del mono, podemos usar nuestras condiciones para que el plátano y el mono estén en la misma posición al mismo tiempo. Para que el mono y el plátano estén en la misma posición, necesitamos\(y_M(t)=y_B(t)\) y\(x_B(t)=x_M(t) =d\) en algún momento\(t\).

Establecer nuestras ecuaciones para\(y_M(t)\) e\(y_B(t)\) iguales entre sí da:

\[\begin{aligned} h-\frac{1}{2} gt^2&=v_{0yB}t-\frac{1}{2}gt^2\\ \therefore h&=v_{0yB}t\end{aligned}\]

Y el ajuste\(x_M(t)=d\) igual a\(x_B(t)\) da:

\[\begin{aligned} \therefore d&=v_{xB}\end{aligned}\]

Podemos simplemente dividir una ecuación entre la otra para encontrar:

\[\begin{aligned} \frac{h}{d}&=\frac{v_{0yB}t}{v_{xB}t}\\ \frac{h}{d}&=\frac{v_{0yB}}{v_{xB}}\end{aligned}\]

Esto nos da la proporción que estamos buscando, así que ahora sabemos que

\[\begin{aligned} \tan\theta&=\frac{h}{d}\\ \therefore \theta&=\tan^{-1}\left(\frac{h}{d}\right)\end{aligned}\]

Este es un resultado algo sorprendente, ya que significa que solo necesitas tirar el plátano en dirección al mono (es decir, apuntar al mono, ¡y tirar!). Así, no importará lo rápido que tires el plátano, y siempre golpearás al mono si apuntas correctamente. Cuando lanzas el plátano más rápido, golpearás al mono más alto en su trayectoria. Si no hay tierra para que el mono golpee, puedes lanzar el plátano tan lentamente como quieras, y eventualmente alcanzará al mono cuando llegue el plátano\(x=d\).

Movimiento relativo

En el capítulo anterior, examinamos cómo convertir la descripción del movimiento de un marco de referencia a otro. Recordemos la situación unidimensional donde describimos la posición de un objeto,\(A\), utilizando un eje\(x\) como\(x^A(t)\). Supongamos que el marco de referencia\(x\),, se mueve con una velocidad constante,\(v'^B\), relativo a un segundo marco de referencia,\(x'\). Encontramos que la posición del objeto se describe en el marco de\(x'\) referencia como:

\[\begin{aligned} x'^A(t)=v'^Bt+x^A(t)\end{aligned}\]

si los orígenes de los dos sistemas coincidieron en\(t=0\). La ecuación anterior simplemente establece que la distancia del objeto al\(x'\) origen es la suma de la distancia desde el\(x'\) origen hasta el\(x\) origen y la distancia desde el\(x\) origen hasta el objeto.

En dos dimensiones, procedemos exactamente de la misma manera, pero usamos vectores en su lugar:

\[\begin{aligned} \vec r'^A(t) = \vec v'^Bt+\vec r^A(t)\end{aligned}\]

donde\(r^A(t)\) es la posición del objeto como se describe en el marco de\(xy\) referencia,\(\vec v'^B\), es el vector de velocidad que describe el movimiento del origen del sistema de\(xy\) coordenadas relativo a un sistema de\(x'y'\) coordenadas y\(\vec r'^A(t)\) es la posición del objeto en el sistema de\(x'y'\) coordenadas. Hemos asumido que los orígenes de los dos sistemas de coordenadas coincidieron en\(t=0\) y que los ejes de los sistemas de coordenadas son\(x\) paralelos (paralelos\(x'\) y\(y\) paralelos a\(y'\)).

Tenga en cuenta que la velocidad del objeto en el\(x'y'\) sistema se encuentra sumando la velocidad de\(xy\) relativo a\(x'y'\) y la velocidad del objeto en el\(xy\) marco (\(\vec v^A(t)\)):

\[\begin{aligned} \frac{d}{dt}\vec r'^A(t) &=\frac{d}{dt}(\vec v'^Bt+\vec r^A(t))\\ &=\vec v'^B+\vec v^A(t)\end{aligned}\]

Como ejemplo, considere la situación representada en la Figura\(\PageIndex{4}\). Brice está en un barco frente a la orilla de Niza, con un sistema de coordenadas\(xy\), y está describiendo la posición de una embarcación que transporta a Alice. Describe la posición de Alice como\(\vec r^A(t)\) en el sistema de\(xy\) coordenadas. Igor está en la orilla y también desea describir la posición de Alice utilizando el trabajo realizado por Brice. Igor ve el movimiento del barco de Brice con una velocidad\(\vec v'^B\) medida en su sistema de\(x'y'\) coordenadas. Para encontrar el vector apuntando a la posición de Alice\(\vec r'^A(t)\), agrega el vector de su origen al origen de Brice (\(\vec v'^B t\)) y el vector de origen de Brice a Alice\(\vec r^A(t)\).

Figura\(\PageIndex{4}\): Ejemplo de conversión de un marco de referencia a otro en dos dimensiones usando adición vectorial.

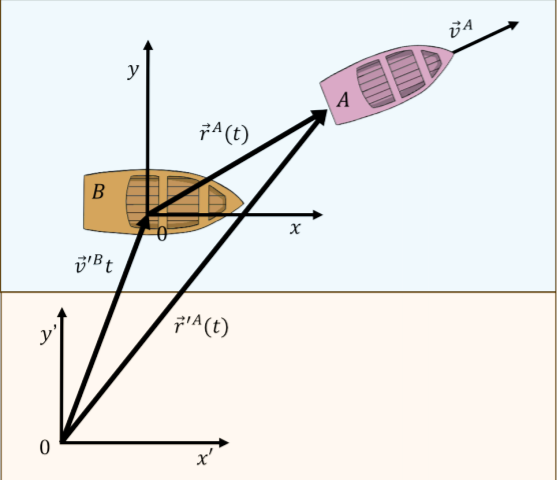
Escribiendo esto por coordenadas, tenemos:

\[\begin{aligned} x'^A(t)&=v'^B_xt+x^A(t)\\ y'^A(t)&=v'^B_yt+y^A(t)\end{aligned}\]

y para las velocidades:

\[\begin{aligned} v_x'^A(t)&=v'^B_x+v_x^A(t)\\ v_y'^A(t)&=v'^B_y+v_y^A(t)\end{aligned}\]

Ejercicio\(\PageIndex{3}\)

Estás en un barco y cruzas un río que fluye hacia el norte, desde la orilla Este hasta la orilla oeste. Señala su embarcación en dirección Oeste y cruza el río. Chloe está viendo tu bote cruzar el río desde la orilla, ¿en qué dirección mide tu vector de velocidad para ser?

1. En dirección Norte.
2. En dirección Oeste.
3. Una combinación de direcciones Norte y Oeste.

Responder

Notas al pie

1. Donde un vector constante significa que tanto la magnitud como la dirección son constantes en el tiempo.