9.2: Teoría Universal de la Gravedad de Newton

Newton supuestamente obtuvo conocimiento de la fuerza gravitacional al observar una manzana cayendo de un árbol y concluyendo que si es la misma fuerza que hace que las manzanas caigan al nivel del mar y en la cima de una montaña, tal vez esa fuerza pueda ejercerse hasta la luna. Es bastante notable que Newton pudo hacer la conexión entre las manzanas que caen y el movimiento de la luna alrededor de la Tierra para encontrar una sola teoría para describir ambas situaciones.

Debemos tener claro que la teoría de la gravedad es una teoría diferente a las “Leyes del movimiento” de Newton (Las tres leyes de Newton). Las Leyes del Movimiento introducen los conceptos de fuerza y masa inercial, y prescriben cómo usar esos conceptos para modelar el movimiento utilizando la cinemática. La Teoría Universal de la Gravedad de Newton es una teoría que describe la fuerza de gravedad que dos cuerpos con masa (gravitacional) ejercen uno sobre el otro.

La Teoría Universal de la Gravedad de Newton establece que si dos cuerpos, con masas\(M_1\) y\(M_2\), ubicados en posiciones\(\vec r_1\) y\(\vec r_2\), respectivamente, están separados por una distancia,\(r\), entonces\(M_2\) ejercerán una fuerza atractiva sobre\(M_1\)\(\vec F_{12}\), dada por:\[\begin{aligned} \vec F_{12}=-G\frac{M_1M_2}{r^2}\hat r_{21}\end{aligned}\] donde\(\hat r_{21}\) es el vector unitario de\(M_2\) a\(M_1\):\[\begin{aligned} \vec r_{21} &= \vec r_2 - \vec r_1\\ \hat r_{21} &= \frac{1}{r} \vec r_{21}\end{aligned}\] como se muestra en la Figura\(\PageIndex{1}\). \(\vec F_{12}\)debe leerse como “la fuerza sobre el cuerpo 1 del cuerpo 2”. \(G=6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2}\)es la Constante Universal de Gravedad de Newton. Cabe señalar que la teoría de Newton para la fuerza de gravedad escrita en esta forma sólo se aplica a masas puntuales (separadas por una distancia\(r\)) o cuerpos esféricos cuyos centros están separados por una distancia\(r\) que es mayor que el radio de cualquiera de las esferas.

Figura\(\PageIndex{1}\): Ilustración de los vectores involucrados en la Teoría Universal de la Gravedad de Newton.

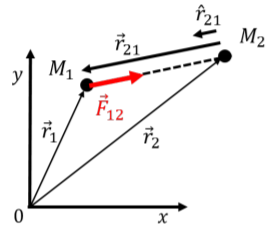
Originalmente, Newton argumentó que la fuerza de gravedad sería proporcional a las masas de los cuerpos, e inversamente proporcional al cuadrado de la distancia entre ellos:\[\begin{aligned} F_{12}\propto \frac{M_1M_2}{r^2}\end{aligned}\] y\(G\) es simplemente la constante de proporcionalidad.

Debido a la Tercera Ley de Newton, el cuerpo 1 ejerce una fuerza sobre el cuerpo 2 que es igual en magnitud pero opuesta en dirección:\[\begin{aligned} \vec F_{12} = -\vec F_{21}\end{aligned}\]

Ejemplo\(\PageIndex{1}\)

Calcular la magnitud de la fuerza de gravedad entre usted y una persona de pie\(50\text{cm}\) from you and compare that to your weight at the surface of the Earth (the force of gravity exerted by the Earth on you).

Solución:

Si asumimos que las dos personas tienen una masa de\(50\text{kg}\), la fuerza de gravedad ejercida por una sobre la otra, si están separadas por\(50\text{cm}\), viene dada por:

\[\begin{aligned} F=G\frac{M_1M_2}{r^2}=(6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2})\frac{(50\text{kg})(50\text{kg})}{(0.5\text{m})^2}=6.67\times 10^{-7}\text{N}\end{aligned}\]

Esta es una fuerza muy pequeña, en comparación con su peso,\(F_g\):

\[\begin{aligned} F_g=M_1g=(50\text{kg})(9.8\text{N/kg})=490\text{N}\end{aligned}\]

que es aproximadamente 700 millones de veces más grande.

Discusión:

La fuerza de gravedad es una fuerza muy débil cuando se compara con otras fuerzas en la Naturaleza, como la fuerza eléctrica entre dos cargas. La Constante Universal de Gravedad de Newton es muy pequeña, por lo que la fuerza de gravedad entre dos objetos es muy pequeña a menos que cualquiera de las masas involucradas sea muy grande, o la distancia entre ellos sea muy pequeña. En general, al modelar el movimiento de los objetos en la Tierra, generalmente es seguro ignorar las fuerzas de gravedad entre los objetos y solo incluir su peso (la fuerza de gravedad de la Tierra).

Ejercicio\(\PageIndex{4}\)

El radio de la Tierra es\(6371\) km. What is the order of magnitude of the Earth’s mass?

1. \(10^{24}\text{kg}\)
2. \(10^{18}\text{kg}\)
3. \(10^{19}\text{kg}\)
4. \(10^{21}\text{kg}\)

No hay suficiente información.

Contestar

Ejemplo\(\PageIndex{2}\)

Determinar la constante en la Tercera Ley de Kepler para los planetas que orbitan el Sol, es decir, el valor de la relación:\[\begin{aligned} \frac{s^3}{T^2}\end{aligned}\] dónde\(s\) está el semieje mayor y\(T\) es el período orbital.

Solución:

Dado que la Tercera Ley de Kepler se sostiene para cualquier cuerpo que orbita el Sol, podemos determinar fácilmente la relación considerando un planeta de masa\(m\) en una órbita circular de\(R\) radio centrada alrededor del Sol. El semieje mayor de la órbita es igual al radio de la órbita para una órbita circular (\(s=R\)).

Si el planeta se encuentra en una órbita circular alrededor del Sol, su velocidad\(v\),, será constante, según la Segunda Ley de Kepler, y así estará ejecutando un movimiento circular uniforme. La única fuerza ejercida sobre el planeta es la fuerza de gravedad ejercida por el Sol. Así la fuerza de gravedad debe ser igual a la masa del planeta por su aceleración radial (centrípeta)\(a_R\), que viene dada por: La Segunda Ley de\[\begin{aligned} a_R=\frac{v^2}{R}\end{aligned}\] Newton para el planeta puede escribirse como:\[\begin{aligned} \sum F = F_g &= ma_R\\ G\frac{Mm}{R^2}&=m\frac{v^2}{R}\\ G\frac{M}{R}&=v^2\end{aligned}\] dónde\(M\) está la masa del Sol. La velocidad del planeta viene dada por la circunferencia de la órbita dividida por el periodo orbital\(T\), ya que es constante:\[\begin{aligned} v=\frac{2\pi R}{T}\end{aligned}\] Reordenando la ecuación a partir de la Segunda Ley de Newton:\[\begin{aligned} G\frac{M}{R}&=v^2\\ G\frac{M}{R}&=\frac{4\pi^2 R^2}{T^2}\\ \therefore \frac{R^3}{T^2}&=G\frac{M}{4\pi^2}\end{aligned}\] Así, encontramos que la relación del cubo del radio orbital al periodo cuadrado es un constante que depende sólo de la masa del Sol, que entonces será la misma para todos los planetas (ya que no depende, digamos, de la masa del planeta que consideramos).

Discusión:

La relación anterior puede, por ejemplo, ser utilizada para determinar la masa del Sol, ya que podemos utilizar la geometría para determinar el semieje mayor para la órbita de un planeta, como lo hizo Kepler con los datos de Tycho Brahe.

Ejemplo\(\PageIndex{3}\)

La aceleración debida a la gravedad de la Tierra depende de la fuerza que la Tierra ejerza sobre un objeto. Utilizando la masa y el radio de la Tierra, determinar la aceleración de los objetos que caen debido a la gravedad de la Tierra en la superficie de la Tierra. También, determinar la altitud donde la aceleración debida a la gravedad de la Tierra es la mitad de la de la superficie terrestre.

Solución:

Podemos encontrar la aceleración debida a la gravedad de la Tierra determinando la aceleración de una masa\(m\) sobre la cual la gravedad es la única fuerza actuante. Es decir, modelamos un objeto que está en caída libre a una\(R\) distancia del centro de la Tierra. La Segunda Ley de Newton se puede utilizar en una dimensión (correspondiente a la dirección que conecta la masa que cae con el centro de la Tierra):\[\begin{aligned} \sum F &= G\frac{Mm}{R^2}=ma\\ \therefore a&=G\frac{M}{R^2}\end{aligned}\] dónde\(M=5.97\times 10^{24}\text{kg}\) está la masa de la Tierra. En la superficie de la Tierra,\(R=R_\oplus=6.371\times 10^{6}\text{m}\):\[\begin{aligned} a&=G\frac{M}{R_\oplus^2}=(6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2})\frac{(5.97\times 10^{24}\text{kg})}{(6.371\times 10^{6}\text{m})^2}\\ &=9.81\text{m/s}^{2}\end{aligned}\] que, por supuesto, es el valor de lo\(g\) que hemos estado usando hasta ahora para la aceleración debido a la gravedad cerca de la superficie de la Tierra. Para encontrar la altitud a la que esto se reduce a la mitad, primero encontramos el valor de\(R\) que corresponde a esta aceleración:\[\begin{aligned} \frac{1}{2}G\frac{M}{R_\oplus^2}&=G\frac{M}{R^2}\\ \therefore R &=\sqrt{2}R_\oplus = 9.0\times 10^{6}\text{m}\end{aligned}\] que corresponde a una altitud de\(h=R-R_\oplus=2640\text{km}\), muy por encima de la atmósfera terrestre.

Discusión:

La aceleración de los objetos que caen disminuye a medida que uno se mueve más lejos del centro de la Tierra. Es así una aproximación asumir que\(g\) es una constante, aunque en la mayoría de los casos esta es una aproximación muy buena. En la práctica, el valor de\(g\) dependerá tanto de la distancia desde el centro de la Tierra como de la composición (densidad) del material en la corteza terrestre por debajo de donde\(g\) se esté midiendo. Las mediciones precisas de la abeja\(g\) han utilizado para determinar la composición de la corteza terrestre y para buscar depósitos minerales y petroleros.

Peso y peso aparente

Probablemente hayas visto imágenes de astronautas flotando alrededor de la Estación Espacial Internacional (ISS) u otras embarcaciones orbitantes, y has oído hablar del término “ingravidez” para describir su movimiento. La ISS se encuentra en órbita a una altitud de aproximadamente\(400\text{km}\), donde la fuerza de la gravedad de la Tierra está lejos de ser insignificante (en el Ejemplo 9.2.3 mostramos que se necesita ir a una altitud de\(2640\text{km}\) para que la fuerza se reduzca a la mitad de la de la superficie de la Tierra). La contradicción entre ser ingrávido y el hecho de que el peso no es cero se resuelve entendiendo que el término popular “ingrávido” es impreciso desde una perspectiva física.

El término correcto para usar desde una perspectiva física es decir que el peso aparente de los astronautas es cero cuando están flotando alrededor. El peso es la magnitud de la fuerza de gravedad ejercida por la Tierra. El peso aparente es, por ejemplo, la fuerza que se mide al estar de pie sobre una báscula de resorte, que es igual a la fuerza normal que ejerce la báscula de resorte sobre la persona. El peso aparente también podría estar determinado por la tensión en una cuerda de la que se suspende a una persona. El peso aparente es la suma de las fuerzas ejercidas sobre una persona menos la fuerza de la gravedad. Si la gravedad es la única fuerza que se ejerce sobre una persona (u objeto), el peso aparente de esa persona es cero, que es lo que popularmente se llama ser ingrávido.

Una forma de sentirse ingrávido es cuando estás en caída libre (por ejemplo, los primeros segundos de un salto en paracaídas desde un avión). Uno puede pensar en estar en órbita como caer continuamente hacia el centro de la Tierra, pero con una velocidad inicial en una dirección tal que en realidad nunca colisionas con la Tierra. La sensación de ingravidez ocurrirá cada vez que la única fuerza que se ejerce sobre ti sea la fuerza de la gravedad. Si estás en una nave espacial en cualquier órbita y la única fuerza sobre la nave espacial es de la gravedad (es decir, ningún cohete o alas está ejerciendo ninguna fuerza), entonces todo en la nave espacial tendrá la misma aceleración, ya que la gravedad es la única fuerza que actúa sobre cualquier cosa en la nave espacial, y aparecerá que todo está flotando. A un observador externo, quedaría claro que la nave espacial y su contenido se están acelerando todos.

Efectos de la rotación de la Tierra

La rotación de la Tierra afecta el peso aparente de los objetos cercanos a la superficie de la Tierra. Considere a una persona de pie en una escala de primavera en el polo Norte (diagrama de cuerpo libre superior en la Figura\(\PageIndex{2}\)). Las únicas dos fuerzas que se ejercen sobre la persona son su peso,\(\vec F_g\), y la fuerza normal,\(\vec N\), ejercida por la báscula de resorte. Dado que la persona no está acelerando, la fuerza normal y el peso tienen la misma magnitud y direcciones opuestas. La báscula leerá así el peso real de la persona ¹.

Figura\(\PageIndex{2}\): El peso aparente, dado por la fuerza normal, es diferente en el ecuador de la Tierra porque la aceleración de una persona es distinta de cero a medida que gira con la Tierra.

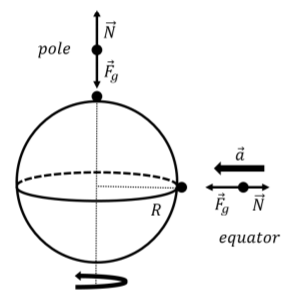
Considera, en cambio, a una persona de pie sobre una escala de resorte en el ecuador (Figura\(\PageIndex{2}\)). Esa persona está acelerando porque está experimentando un movimiento circular uniforme a medida que gira junto con la Tierra. Nuevamente, las únicas fuerzas que actúan sobre la persona son su peso y la fuerza normal que ejerce la báscula. La suma de las fuerzas ahora debe ser igual a la masa de la persona,\(m\), veces la aceleración radial,\(a_r\), eso es necesario para que sigan la superficie de la Tierra a medida que la Tierra gira alrededor de su eje. La Segunda Ley de Newton nos permite encontrar la magnitud de la fuerza normal que actúa sobre la persona:\[\begin{aligned} \sum F &= F_g-N=ma_r=m\frac{v^2}{R}\\ \therefore N &= F_g - m\frac{v^2}{R}\\ &=G\frac{Mm}{R^2} - m\frac{v^2}{R}\\ &=m\left(G\frac{M}{R^2} - \frac{v^2}{R} \right)\\ &=m\left(g - \frac{v^2}{R} \right)\end{aligned}\] dónde\(M\) está la masa de la Tierra,\(R\) es el radio de la Tierra, y\(v\) es la velocidad en la superficie de la Tierra debido a la rotación de la Tierra. En la última línea, se utilizó el resultado del Ejemplo 9.2.3 donde determinamos el valor de\(g\) en términos de la masa y radio de la Tierra.

Vemos que la fuerza normal se reduce en comparación con lo que sería si la Tierra no estuviera rotando (\(v=0\)) o si uno está parado en uno de los polos. Su peso aparente, que puede medir estando de pie en una escala de resorte, es así más pequeño en el ecuador que en los polos. La cantidad entre paréntesis se puede considerar como un valor modificado o “efectivo” de\(g\) en el ecuador.

Ejercicio\(\PageIndex{5}\)

¿Cuál es el valor efectivo de\(g\) at the equator?

1. \(9.80 \text{m/s}^2\)
2. \(9.78 \text{m/s}^2\)
3. \(9.70 \text{m/s}^2\)
4. \(9.51 \text{m/s}^2\)

Contestar

Si estás dando vueltas a la Tierra a una\(R\) distancia del centro de la Tierra a una velocidad constante\(v\), es posible que tu peso aparente sea cero. Imagínese pararse en una báscula en una aeronave que está dando vueltas a la Tierra y midiendo su peso aparente con la báscula de resorte. A medida que aumenta la velocidad de la aeronave, tu peso aparente\(N\),, disminuye de acuerdo con la fórmula que acabamos de encontrar:\[\begin{aligned} N=m\left(G\frac{M}{R^2} - \frac{v^2}{R} \right)\end{aligned}\] A cierta velocidad,\(v\), tu peso aparente es cero y te sientes ingrávido:\[\begin{aligned} G\frac{M}{R^2} &= \frac{v^2}{R}\\ \therefore v&= \sqrt{G\frac{M}{R} }\end{aligned}\] Esta velocidad corresponde a un centrípeta aceleración que es exactamente igual a la debida a la gravedad. Esto tiene sentido, ya que la gravedad es la única fuerza que está actuando sobre ti (la fuerza normal ahora es cero), que es exactamente lo que llamamos estar en órbita.

La rotación de la Tierra tiene algunas consecuencias interesantes para los objetos estacionarios. En cualquier posición de la Tierra que no esté en el ecuador o en los polos, la suma de las fuerzas sobre cualquier objeto estacionario (es decir, estacionario en relación con la superficie de la Tierra) no puede ser cero. Esto se debe a que el objeto debe rotar junto con la Tierra, por lo que la fuerza neta sobre el objeto debe apuntar hacia el centro del círculo alrededor del cual está girando esa ubicación en la Tierra.

Tomemos, por ejemplo, una plomada, que consiste en una masa que cuelga de una cuerda. Las dos fuerzas que actúan sobre la masa son la gravedad y la tensión. La fuerza de gravedad debe apuntar hacia el centro de la Tierra. Esperaríamos que la fuerza de la tensión, y por lo tanto la cuerda, apuntara directamente lejos del centro de la Tierra. No obstante, encontramos que si la plomada se ubica en algún ángulo\(\theta\) del ecuador (pero no en el ecuador ni en los polos), como en la Figura\(\PageIndex{3}\), entonces la cuerda apuntará ligeramente alejada del centro de la Tierra. Para que la masa permanezca estacionaria con relación al suelo, debe girar junto con la Tierra (radio\(R\)) alrededor de un círculo de radio\(R\cos\theta\). Así, la tensión de la cuerda no puede apuntar lejos del centro de la Tierra, porque la fuerza neta debe apuntar hacia el centro del círculo de radio\(R\cos\theta\).

Figura\(\PageIndex{3}\): Alejado del ecuador y los polos, una plomada (derecha) no apunta hacia el centro de la Tierra, debido a que la fuerza neta sobre la masa debe proporcionar la aceleración hacia el centro del círculo (de radio\(Rcos θ\)) alrededor del cual gira la plomada debido a la rotación de la Tierra. Tenga en cuenta que la deflexión de la plomada es muy exagerada.

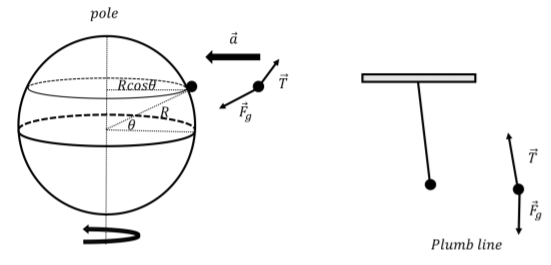
Ejercicio\(\PageIndex{6}\)

Cortas la cuerda de la plomada. ¿Dónde aterriza la masa en relación con su latitud inicial (el ángulo\(\theta\) in Figure \(\PageIndex{3}\))?

1. A la misma latitud.
2. Más cerca del polo más cercano.
3. Más cerca del ecuador.

Contestar

El campo gravitacional

La fuerza gravitacional ejercida sobre una masa\(m\) por una masa\(M\) puede escribirse como:\[\begin{aligned} \vec F(\vec r) = -G\frac{Mm}{r^2}\hat r\end{aligned}\] si definimos un sistema de coordenadas con el origen ubicado en el centro de la masa\(M\) para que\(\vec r\) sea la posición de\(m\) relativo a\(M\). Podemos definir el “campo gravitacional”, en posición\(\vec g(\vec r)\)\(\vec r\), debido a la presencia de masa\(M\) como la fuerza gravitacional por unidad de masa ejercida por\(M\):

\[\vec g(\vec r)=\frac{\vec F(\vec r)}{m}=-G\frac{Mm}{r^{2}}\hat r\]

La palabra “campo” es solo un término matemático para una función que depende de la posición. Dado que\(\vec g(\vec r)\) es un vector, nos referiríamos a él como un “campo vectorial”.

Definir el campo gravitacional facilita el cálculo de la fuerza de gravedad a partir\(M\) de cualquier masa\(m\):\[\begin{aligned} \vec F_g = m\vec g(\vec r)\end{aligned}\]

En la superficie de la Tierra, la magnitud del campo gravitacional viene dada por:\[\begin{aligned} g(R_\oplus)=\frac{GM}{R_\oplus^2}=9.81\text{N/kg}\end{aligned}\] dónde\(R_\oplus\) está el radio de la Tierra. Por supuesto, esto también corresponde a la aceleración de objetos en caída libre cerca de la superficie de la Tierra, que podemos encontrar a partir de la Segunda Ley de Newton:\[\begin{aligned} \sum \vec F &= \vec F_g = m\vec a\\ m\vec g(R_\oplus)&= m\vec a\\ \therefore \vec a &= \vec g(R_\oplus)\end{aligned}\] pero vemos aquí por qué es más preciso referirse\(g\) como la “magnitud del campo gravitacional en la superficie de la Tierra” en lugar de “la aceleración debida a la gravedad de la Tierra”. También vale la pena señalar que los dos solo son iguales si la masa gravitacional (a la izquierda de la ecuación en la segunda línea) es la misma que la masa inercial (a la derecha de la ecuación). La masa gravitacional es la masa que aparece en la fuerza gravitacional definida por Newton, mientras que la masa inercial es la masa que aparece con la aceleración en la Segunda Ley de Newton.

Ejercicio\(\PageIndex{7}\)

Dos pequeños objetos con diferentes masas,\(m_1\) and \(m_2\), are located a distance \(r\) from a nearby star. What can you say about the magnitude of the gravitational field and the magnitude of the gravitational force on \(m_1\) and \(m_2\)?

1. El campo es diferente y las fuerzas son diferentes.
2. El campo es diferente pero las fuerzas son las mismas.
3. El campo es el mismo pero las fuerzas son distintas.
4. El campo es el mismo y las fuerzas son las mismas.

Contestar

Supongamos que hay dos grandes cuerpos de masa,\(M_1\) y\(M_2\), y un cuerpo de masa más pequeño,\(m\). Podemos calcular la fuerza gravitacional neta en\(m\) sumando los vectores de fuerza gravitacional de\(M_1\) y\(M_2\) por separado. Si los campos gravitacionales de\(M_1\) y\(M_2\) están dados por\(\vec g_1(\vec r)\) y\(\vec g_2(\vec r)\), respectivamente, entonces la fuerza gravitacional total en\(m\) viene dada por:\[\begin{aligned} \vec F &= m\vec g_1(\vec r) + m\vec g_2(\vec r)=m(\vec g_1(\vec r)+\vec g_2(\vec r))\\ &=m \vec g(\vec r)\end{aligned}\] donde hemos introducido el total gravitacional campo:\[\begin{aligned} \vec g(\vec r) = \vec g_1(\vec r)+\vec g_2(\vec r)\end{aligned}\] En otras palabras, si hay múltiples cuerpos que resultan en una fuerza de gravedad no despreciable, podemos calcular sus campos gravitacionales de forma independiente y sumarlos juntos para definir un campo gravitacional neto,\(\vec g(\vec r)\), que modela la fuerza neta de la gravedad de todos los cuerpos. La fuerza gravitacional neta sobre un nuevo cuerpo de masa\(m'\) viene entonces simplemente dada por\(m'\vec g(\vec r)\), y no necesitamos sumar más vectores juntos. Por ejemplo, al calcular el movimiento de satélites que pueden ser influenciados por la fuerza de gravedad tanto de la Tierra como de la Luna, simplemente necesitamos calcular el campo gravitacional neto de la Tierra y la Luna, y el movimiento de cualquier satélite puede modelarse entonces usando ese campo gravitacional neto.

Ejercicio\(\PageIndex{8}\)

T aquí hay dos planetas con igual masa ubicados a una distancia\(d\) apart. Position \(A\) is located midway between the two planets. Position \(B\) is located a distance \(d/2\) from one of the planets, in the position shown in Figure \(\PageIndex{4}\). How does the field at \(A\) compare to the field at \(B\)?

Figura\(\PageIndex{4}\): Dos planetas están a una distancia de\(d\) distancia. Estamos considerando el campo gravitacional en dos posiciones,\(A\) y\(B\), ubicado cerca de los planetas.

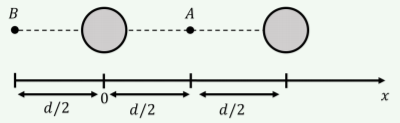
1. La magnitud del campo es la misma en\(A\) y\(B\).
2. La magnitud del campo es mayor a\(A\) que at\(B\).
3. La magnitud del campo es mayor a\(B\) que at\(A\).

Contestar

Ley de Gauss

La Teoría Universal de la Gravedad de Newton postula que la fuerza de gravedad entre dos cuerpos disminuye a medida que el cuadrado de la distancia entre esos dos cuerpos disminuye. Usando la terminología de un campo, diríamos que la fuerza del campo gravitacional de un objeto disminuye a medida que la inversa del cuadrado de la distancia a ese objeto disminuye. Este es un ejemplo de lo que generalmente llamamos una “ley de cuadrados inversos”. La fuerza eléctrica entre dos cargas también viene dada por una ley de cuadrados inversos, y ahora entendemos que estas fuerzas se comportan como si fueran “transmitidas” por ondas o partículas.

Si una fuerza viene dada por una ley de cuadrado inverso, entonces la Ley de Gauss da una manera de determinar la fuerza del campo que está asociada a esa fuerza. En el caso de la gravedad, la Ley de Gauss establece que:\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A = 4\pi G M^{enc}\end{aligned}\] donde la integral de la izquierda es una integral sobre una “superficie cerrada” que rodea completamente la masa para la que queremos determinar el campo gravitacional. Para evaluar la integral, imagínese tomar una superficie cerrada\(S\),, que rodea la masa. El vector\(d\vec A\) se define como el vector que va con un pequeño elemento de esa superficie y apunta hacia afuera desde la superficie cerrada. La magnitud del vector es igual al área de esa pequeña superficie (\(dA\)), como se ilustra en la Figura\(\PageIndex{5}\). Luego se puede tomar el producto escalar de\(d\vec A\) con el campo gravitacional,\(\vec g(\vec r)\), en ese punto de la superficie. Si suma todos esos productos escalares, obtiene el valor de la integral a la izquierda. La Ley de Gauss establece que el valor de esa integral es igual\(4 \pi G\) por la masa total que está encerrada por la superficie.

Pensamientos de Olivia

Si quieres saber si una superficie está cerrada, pregúntate si podrías poner agua dentro de la superficie y no estar preocupado de que se derrame. Por ejemplo, si pones agua en una esfera o un cubo, el agua no se derramaría aunque la sacudieras, por lo que son superficies cerradas. Un cuadrado plano es una superficie abierta porque no hay “dentro” en el que incluso meter el agua. Un cuenco es una superficie abierta porque, aunque se puede poner agua en él, el agua podría derramarse.

Entraremos en más detalles sobre la Ley de Gauss cuando cubramos el electromagnetismo, pero vale la pena ver cómo usarlo en un escenario sencillo. La figura\(\PageIndex{5}\) muestra un cuerpo esférico de masa\(M\) y radio\(R\) para el cual nos gustaría determinar el valor del campo gravitacional a una\(r\) distancia del centro del cuerpo.

Figura\(\PageIndex{5}\): Ejemplo de una superficie gaussiana esférica,\(S\), de radio\(r\) centrada alrededor de un cuerpo de masa\(M\) y radio\(R\). Un elemento de la superficie, también\(d\vec A\) se muestra junto con el campo gravitacional,\(\vec g(\vec r)\), en ese punto.

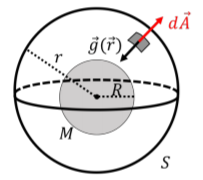
Para ello, dibujamos una “superficie gaussiana”\(S\), es decir, una esfera con un radio\(r\), y centrada alrededor del cuerpo. En cualquier punto de la superficie, el vector del elemento de área\(d\vec A\) apunta lejos del centro de la superficie esférica. El vector de campo gravitacional, siempre\(\vec g(\vec r)\) apuntará hacia el centro de la superficie esférica, como se ilustra. Además, por simetría, la magnitud de\(\vec g(\vec r)\) es constante a lo largo de toda la superficie gaussiana. Así, el producto escalar\(\vec g(\vec r) \cdot d\vec A=-g(r)dA\) en todas partes a lo largo de la superficie (es negativo porque los dos vectores son antiparalelos). Así, la integral viene dada por:

\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A = -g(r)\oint dA \end{aligned}\]

donde factorizamos\(g(r)\) fuera de la integral, ya que la magnitud de\(\vec g(\vec r)\) es constante para todos los elementos del área\(dA\) en la esfera. Recuerda que una integral es una suma. La integral significa\(\oint dA\) así “suma todos los elementos del área\(dA\) sobre toda la superficie\(S\)”. Así, la integral es el área total de la superficie esférica\(S\)²:

\ [\ comenzar {alineado}\ oint\ vec g (\ vec r)\

d\ vec A = -g (r)\ oint dA =-g (r) (4\ pi r^2)\ final {alineado}\]

Insertando esto en la Ley de Gauss, encontramos:\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A &= 4\pi G M^{enc}\\ -g(r)(4\pi r^2) &= 4\pi G M^{enc}\\ \therefore g(r) &= - \frac{GM}{r^2}\end{aligned}\] dónde\(M^{enc}=M\) está la masa total encerrada por la superficie gaussiana (en este caso, toda la masa\(M\) está encerrada). Este es por supuesto el resultado que esperábamos y obtuvimos antes de la formulación de Newton. Tenga en cuenta que la Ley de Gauss solo es fácil de usar si el sistema es altamente simétrico (por ejemplo, esféricamente simétrico), y que no da la dirección del vector de campo, que debe obtenerse a partir de argumentos de simetría.

Pensamientos de Olivia

Aquí hay una analogía para describir la Ley de Gauss para la gravedad: Una celebridad famosa está haciendo un evento, y atraen a cierto número de fans que quieren acercarse lo más posible a la celebridad. Pusiste una barricada alrededor de la celebridad. El campo gravitacional está representado por lo abarrotado que está en algún lugar a lo largo de la barricada. Si una segunda celebridad está en el evento, atraerán a sus propios fans, por lo que habrá más gente alrededor de la barricada. El número de celebridades es algo así como la misa cerrada\(M^{enc}\).

Un fotógrafo viene al evento, y usted le dijo que se parara en algún lugar que está a una\(r\) distancia de las celebridades. El fotógrafo quiere saber qué tan concurrido estará cuando esté parado detrás de la barricada en ese lugar. La ley de Gauss nos da una manera de resolverlo. Si sabes qué celebridades están en el evento (\(M^{enc}\)), puedes determinar cuántas personas habrá ahí (esto es como encontrar\(4\pi GM^{enc}\)). Entonces, si puedes construir una barricada de tal manera que los abanicos se distribuyan uniformemente a su alrededor, y sabes cuánto dura esa barricada (\(\oint dA\)), puedes calcular fácilmente qué tan abarrotada estará en algún momento a lo largo de la barricada (solo puedes dividir el número de personas por la longitud de la barricada). La barricada representa nuestra superficie gaussiana y, como una superficie gaussiana, puede ser la forma que queramos siempre que encierra a las celebridades y pase por el punto que nos interesa. Si queremos asegurarnos de que la gente esté distribuida de manera uniforme, la forma de la barricada va a depender del caso específico. Tomemos el ejemplo de nuestro único cuerpo esférico. Esto es analago a tener una celebridad en el evento.

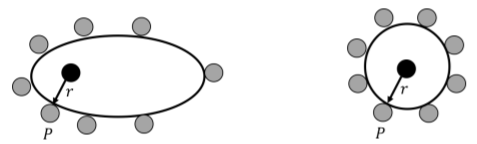
La figura\(\PageIndex{6}\) muestra dos barricadas posibles que podríamos construir. Aunque técnicamente podemos construir la barricada de la izquierda, no nos ayuda porque las zonas más cercanas a la celebridad estarán más abarrotadas. En cambio, queremos construir la barricada a la derecha, que es un círculo de radio\(r\), porque los ventiladores están uniformemente distribuidos. Es por ello que utilizamos una superficie gaussiana esférica cuando estamos considerando el campo debido a un cuerpo esférico - en cualquier punto a una\(r\) distancia del cuerpo, el campo será el mismo. (Nota: Recuerda que, a diferencia de la barricada, la superficie gaussiana no es cosa física, por lo que no afectará al campo gravitacional. Es sólo una herramienta matemática que nos permite aprovechar lo que ya se ve el campo).

Figura\(\PageIndex{6}\): Una celebridad (punto negro) atrae a los fans (puntos grises). Un fotógrafo (punto etiquetado como “\(P\)”) se encuentra detrás de la barricada a una\(r\) distancia. Esto muestra dos posibles barricadas que podríamos construir alrededor de la celebridad. La densidad de los abanicos no es uniforme para la barricada de la izquierda, por lo que no elegiríamos esa forma para evaluar la integral gaussiana.

También podemos usar la Ley de Gauss para determinar el campo gravitacional dentro del cuerpo de masa\(M\) y radio\(R\). Esto se ilustra en la Figura\(\PageIndex{7}\), que muestra una superficie gaussiana esférica de radio\(r\) que se encuentra dentro del cuerpo de masa\(M\).

Figura\(\PageIndex{7}\): Ejemplo de una superficie gaussiana esférica,\(S\), de radio\(r\) centrada dentro de un cuerpo de masa\(M\) y radio\(R\).

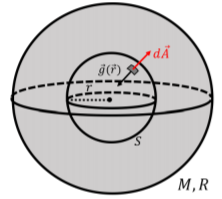
El campo gravitacional dentro del cuerpo de masa también\(M\) es simétrico y de magnitud constante a través de toda la superficie, de manera que la integral es la misma que antes:\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A=-g(r)(4\pi r^2)\end{aligned}\] Sin embargo, para usar la Ley de Gauss, necesitamos determinar la masa del cuerpo que está encerrada dentro del superficie esférica, que será menor que\(M\). Si asumimos que la densidad de masa\(\rho\),, del objeto es constante (el cuerpo está hecho de un material uniforme), entonces la densidad es simplemente la masa del objeto sobre su volumen:\[\begin{aligned} \rho = \frac{M}{\frac{4}{3}\pi R^3}\end{aligned}\] La cantidad de masa encerrada por la superficie esférica de radio\(r\) es la densidad multiplicado por el volumen de una esfera de radio\(r\):\[\begin{aligned} M^{enc} = \rho \frac{4}{3}\pi r^3 = M\frac{r^3}{R^3}\end{aligned}\] Aplicando la Ley de Gauss, ahora podemos encontrar la magnitud del campo gravitacional dentro del cuerpo esférico a una\(r\) distancia del centro:\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A &= 4\pi G M^{enc}\\ -g(r)(4\pi r^2) &= 4\pi G M\frac{r^3}{R^3}\\ \therefore g(r) &= - \frac{G M}{R^3}r\end{aligned}\] Y encontramos que, dentro de un cuerpo esférico uniforme de masa\(M\), el campo gravitacional aumenta linealmente con el radio a medida que uno se mueve fuera del centro. En el centro del cuerpo, el campo gravitacional es cero.

Ejercicio\(\PageIndex{9}\)

¿Qué se puede decir de la magnitud del campo gravitacional dentro de una capa esférica de masa\(M\)?

1. Aumenta a medida que te mueves del centro de la concha esférica.
2. Disminuye a medida que te mueves del centro de la concha esférica.
3. Es igual a cero.
4. Es distinto de cero y de magnitud constante.

Contestar

Notas al pie

1. El peso que se muestra en la báscula es igual en magnitud a la fuerza normal que ejerce la báscula sobre la persona. Es la fuerza de reacción a esa fuerza normal.

2. El área de superficie de una esfera de radio\(r\) es\(4πr^{2}\).