11.6: Momento de inercia

Para modelar cómo un objeto gira alrededor de un eje, utilizamos la Segunda Ley de Newton para la dinámica rotacional:\[\begin{aligned} \vec\tau^{ext} = I \vec \alpha\end{aligned}\] dónde\(\vec\tau^{ext}\) está el par externo neto ejercido sobre el objeto alrededor del eje de rotación,\(\vec \alpha\) es la aceleración angular del objeto, y \(I\)es el momento de inercia del objeto (alrededor del eje). Si consideramos que el objeto está hecho de muchas partículas de masa\(m_i\) cada una ubicada en una posición\(\vec r_i\) relativa al eje de rotación, el momento de inercia se define como:\[\begin{aligned} I = \sum_i m_i r_i^2\end{aligned}\] Consideremos, por ejemplo, el momento de inercia de una varilla de masa uniforme \(M\)y longitud\(L\) que se gira alrededor de un eje perpendicular a la varilla que pasa por uno de los extremos de la varilla, como se representa en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Varilla de longitud\(L\) y masa\(M\) que gira alrededor de un eje perpendicular a la varilla que atraviesa uno de sus extremos.

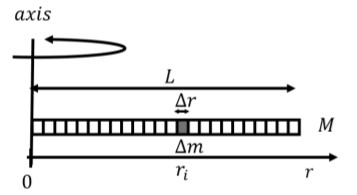
Introducimos la densidad de masa lineal de la varilla\(\lambda\),, como la masa por unidad de longitud:\[\begin{aligned} \lambda = \frac{M}{L}\end{aligned}\] Modelamos la varilla como hecha de muchos elementos de masa pequeña de masa\(\Delta m\), de longitud\(\Delta r\), en una ubicación\(r_i\), como se ilustra en la Figura \(\PageIndex{1}\). Usando la densidad de masa lineal, el elemento de masa\(\Delta m\),, tiene una masa de:\[\begin{aligned} \Delta m = \lambda \Delta r\end{aligned}\] La varilla está hecha de muchos de esos elementos de masa, y el momento de inercia de la varilla viene así dado por:\[\begin{aligned} I &= \sum_i \Delta m r_i^2 =\sum_i \lambda \Delta r r_i^2\end{aligned}\] Si tomamos el límite en el que la longitud del elemento de masa es infinitesimalmente pequeña ( \(\Delta r \to dr\)) la suma puede escribirse como una integral sobre la dimensión de la varilla:\[\begin{aligned} I &= \int_0^L\lambda r_i^2dr = \frac{1}{3}\lambda L^3 = \frac{1}{3}\left( \frac{M}{L} \right)L^3 \\ &=\frac{1}{3} ML^2\end{aligned}\] donde reexpresamos la densidad de masa lineal en términos de la masa y longitud de la varilla. En general, podemos escribir el momento de inercia de un objeto continuo como:\[\begin{aligned} I = \int r^2 dm \end{aligned}\] donde\(dm\) está un pequeño elemento de masa que conforma el objeto,\(r\) es la distancia desde ese elemento de masa al eje de rotación, y la integral está sobre la dimensión del objeto. Como lo hicimos anteriormente, normalmente estableceríamos esta integral para que eso\(dm\) se exprese en términos de\(r\) para que podamos asumir una integral sobre\(r\).

Ejemplo\(\PageIndex{1}\)

Calcular el momento de inercia de un anillo de masa delgado uniforme\(M\) and radius \(R\), rotated about an axis that goes through its center and is perpendicular to the disk.

Solución:

Tomamos un pequeño elemento\(dm\) de masa del anillo, como se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Un elemento de masa pequeña sobre un anillo.

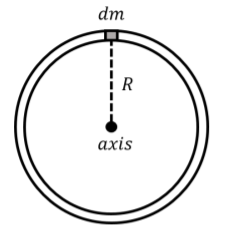
El momento de inercia viene dado por:\[\begin{aligned} I = \int dm r^2\end{aligned}\] En este caso, cada elemento de masa alrededor del anillo estará a la misma distancia del eje de rotación. El valor\(r^2\) en la integral es una constante sobre todo el anillo, y así se puede sacar de la integral:\[\begin{aligned} I = \int dm r^2 = R^2\int dm\end{aligned}\] donde usamos el hecho de que el anillo tiene un radio\(R\), por lo que la distancia\(r\) de cada elemento de masa al eje de rotación es \(R\). La integral:\[\begin{aligned} \int dm\end{aligned}\] solo significa “suma todos los elementos de masa\(dm\)”, y por lo tanto es igual a\(M\), la masa total del anillo. El momento de inercia del anillo es así:\[\begin{aligned} I = R^2\int dm = MR^2\end{aligned}\]

El teorema del eje paralelo

El momento de inercia de un objeto sólido puede ser difícil de calcular, especialmente si el objeto no es simétrico. El teorema del eje paralelo nos permite determinar el momento de inercia de un objeto alrededor de un eje, si ya conocemos el momento de inercia del objeto alrededor de un eje que es paralelo y pasa por el centro de masa del objeto.

Consideremos un objeto para el que conocemos el momento de inercia,\(I_{CM}\), alrededor de un eje que atraviesa el centro de masa del objeto. Definimos un sistema de coordenadas tal que el origen se ubica en el centro de masa, y el\(z\) eje es paralelo al eje alrededor del cual conocemos el momento de inercia, como se ilustra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Un objeto con un sistema de coordenadas cuyo origen está en el centro de masa del objeto, y para el cual conocemos el momento de inercia alrededor del\(z\) eje. Deseamos determinar el momento de inercia del objeto a través de un segundo eje, paralelo al\(z\) eje, pero ubicado a una distancia h del centro de masa.

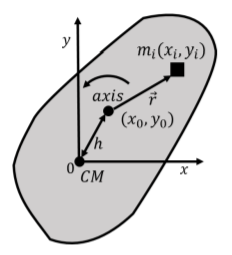
Deseamos determinar el momento de inercia para el objeto para un eje que es paralelo al\(z\) eje, pero que atraviesa un punto con coordenadas\((x_0,y_0)\) ubicadas a una\(h\) distancia del centro de masa. El momento de inercia alrededor de un eje paralelo al\(z\) eje y que atraviesa ese punto,\(I_h\) viene dado por:\[\begin{aligned} I_h = \sum_i m_i r_i^2\end{aligned}\] donde\(m_i\) se encuentra un elemento de masa del objeto ubicado a una\(r_i\) distancia del eje de rotación. Si el elemento de masa se encuentra en una posición\((x_i,y_i)\) relativa al centro de masa, podemos escribir la distancia\(r_i\) en términos de la posición del elemento de masa, y de la posición del eje de rotación:\[\begin{aligned} r_i^2 = (x_i-x_0)^2+(y_i-y_0)^2 = x_i^2-2x_ix_0+x_0^2+y_i^2-2y_iy_0+y_0^2\end{aligned}\] Obsérvese que:\[\begin{aligned} x_0^2 + y_0^2 = h^2\end{aligned}\] El momento de inercia, \(I_h\), se puede escribir así como:\[\begin{aligned} I_h &= \sum_i m_i r_i^2 =\sum_i (m_i(x_i^2+ y_i^2)-2x_0m_ix_i-2y_0m_iy_i+m_ih^2)\\ &=\sum_i m_i(x_i^2+ y_i^2) + h^2\sum_i m_i - 2x_0 \sum_im_ix_i- 2y_0 \sum_im_iy_i\end{aligned}\] donde dividimos la suma en varias sumas, y factorizamos términos constantes (\(h\),\(x_0\),\(y_0\)) fuera de las sumas, ya que estas constantes no dependen de qué elemento de masa estemos considerando. El primer término es el momento de inercia alrededor del centro de masa, ya que\(x_i^2+y_i^2\) es la distancia al centro de masa. El segundo término es\(h^2\) veces la masa total del objeto, ya que la suma de todos los\(m_i\) es solo la masa\(M\),, del objeto. Ahora considera el término: ¡\[\begin{aligned} -2x_0 \sum_im_ix_i\end{aligned}\]La suma,\(\sum m_i x_i\) es el numerador en la definición de la\(x\) coordenada del centro de masa! La suma es así cero, porque elegimos el origen para que se ubique en el centro de masa. Los dos últimos términos en la suma son así idénticamente cero, ¡porque corresponden a las\(y\) coordenadas\(x\) y del centro de masa!

Así podemos escribir el teorema del eje paralelo:

\[I_{h}=I_{CM}+Mh^{2}\]

donde\(I_{CM}\) es el momento de inercia de un objeto de masa\(M\) alrededor de un eje que atraviesa el centro de masa y,\(I_h\), es el momento de inercia alrededor de un segundo eje que es paralelo al primero y a una\(h\) distancia.

Ejemplo\(\PageIndex{2}\)

En el apartado anterior, calculamos el momento de inercia de una varilla de longitud\(L\) and mass \(M\) through an axis that is perpendicular to the rod and through one of its ends, and found that it was given by:

\[\begin{aligned} I=\frac{1}{3}ML^2\end{aligned}\]

¿Cuál es el momento de inercia de la varilla alrededor de un eje que es perpendicular a la varilla y pasa por su centro de masa?

Solución:

En este caso, conocemos el momento de inercia a través de un eje que no pasa por el centro de masa. El centro de masa se ubica a una\(h=L/2\) distancia del punto sobre el que conocemos el momento de inercia,\(I_h\).

Usando el teorema del eje paralelo, podemos encontrar el momento de inercia a través del centro de masa:\[\begin{aligned} I_{CM} &= I_h - Mh^2\\ &=\frac{1}{3}ML^2 - M \left( \frac{L}{2}\right)^2 = \frac{1}{12}ML^2\end{aligned}\]

Discusión:

Encontramos que el momento de inercia alrededor del centro de masa es menor que el momento de inercia alrededor del extremo de la varilla. Esto tiene sentido porque al girar la varilla alrededor de su extremo, más de su masa se aleja más del eje de rotación, lo que se traduce en un mayor momento de inercia.