11.7: Equilibrio

En esta sección, consideramos las condiciones bajo las cuales un objeto se encuentra en equilibrio estático o dinámico. Un objeto está en equilibrio si no gira cuando se ve en un marco de referencia donde el centro de masa del objeto es estacionario (o se mueve a velocidad constante).

Equilibrio estático

Un objeto está en equilibrio estático, si tanto la suma de las fuerzas externas ejercidas sobre el objeto como la suma de los pares externos (alrededor de cualquier eje) son cero. Si el objeto está en equilibrio estático el centro de masa no tendrá aceleración y el objeto no tendrá aceleración angular. En el marco de referencia del centro de masa, el objeto está inmóvil.

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{1}\): Dos masas en una balanza.

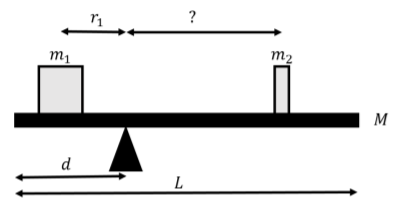
Dos masas,\(m_1\) y\(m_2\) se colocan en una balanza como se muestra en la Figura\(\PageIndex{1}\). La balanza está hecha de una tabla de masa\(M\) y longitud\(L\) que se coloca sobre un fulcro que está a una\(d\) distancia de uno de los bordes de la tabla. Si la masa\(m_1\) se coloca a una\(r_1\) distancia del fulcro, ¿qué tan lejos\(m_2\) se debe colocar la masa en el otro lado de la tabla para que la balanza esté en equilibrio?

Solución:

Podemos considerar la tabla como el objeto que se encuentra en equilibrio estático. Así, la suma de las fuerzas y la suma de los pares en la tabla debe ser cero. Comenzamos identificando las fuerzas que se ejercen sobre la tabla; estas son:

1. \(\vec F_g\), el peso de la tabla, ejercida en el centro de masa de la tabla.
2. \(\vec F_1\), una fuerza igual al peso de la masa\(m_1\), ejercida en la ubicación de\(m_1\).
3. \(\vec F_2\), una fuerza igual al peso de la masa\(m_2\), ejercida en la ubicación de\(m_2\).
4. \(\vec N\), una fuerza normal ejercida por el fulcro.

Las fuerzas se ilustran en la Figura\(\PageIndex{2}\) junto con nuestra elección del sistema de coordenadas. El\(z\) eje no está ilustrado, y se dirige fuera de la página.

Figura\(\PageIndex{2}\): Fuerzas ejercidas sobre la tabla.

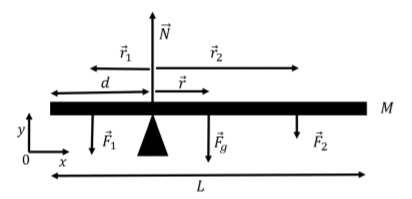
Todas las fuerzas están en la\(y\) dirección, por lo que solo escribimos el\(y\) componente de la Segunda Ley de Newton (con aceleración cero), lo que nos permite determinar la magnitud de la fuerza normal:\[\begin{aligned} \sum F_y = N - Mg -m_1g - m_2 g &=0\\ \therefore N &= (M+m_1+m_2) g\end{aligned}\]

Debido a que la tabla está en equilibrio estático, la suma de los pares también debe ser cero. Podemos elegir el eje de rotación sobre el cual calcular los pares. Elegimos un eje que es paralelo al\(z\) eje (fuera de la página) y pasa por el fulcro. En general, ya que podemos elegir el eje de rotación, suele ser conveniente elegir un eje que pase por un punto donde se esté ejerciendo al menos una fuerza, porque el par de esa fuerza será cero (su brazo de palanca será cero). Además, dado que todas las fuerzas están en el\(xy\) plano, el par neto en la tabla estará en la\(z\) dirección, por lo que tiene sentido elegir un eje en esa dirección.

Los pares del peso de la tabla y de la fuerza ejercida por la masa\(m_2\) estarán en la\(z\) dirección negativa, y el par de torsión de la fuerza ejercida por la masa\(m_1\) estará en la\(z\) dirección positiva. La fuerza normal no dará como resultado ningún par, ya que se ejerce en el eje de rotación y tiene un brazo de palanca de cero.

Definimos\(\vec r_1\) como el vector desde el fulcro hasta la masa\(m_1\). El par,\(\vec \tau_1\), de la fuerza ejercida por la masa\(m_1\) viene dado por:\[\begin{aligned} \vec \tau_1 &= \vec r_1 \times \vec F_1 = (-r_1 \hat x) \times (-F_1 \hat y) \\ &= r_1F_1(\hat x \times \hat y) = r_1F_1\hat z=r_1m_1g\hat z\end{aligned}\] donde se utilizó el hecho de que la magnitud de\(\vec F_1\) es\(m_1 g\). De igual manera, los pares de torsión de la fuerza ejercida por\(m_2\)\(\vec\tau_2\), y por el peso\(\vec\tau_g\), vienen dados por:\[\begin{aligned} \vec \tau_2 &=\vec r_2 \times \vec F_2 = -m_2 g r_2 \hat z\\ \vec \tau_g &=\vec r \times \vec F_g=-rMg\hat z = -\left(\frac{L}{2}-d\right)Mg\hat z\end{aligned}\] dónde\(\frac{L}{2}-d\) está la distancia entre el fulcro y donde se ejerce el peso de la tabla. Requerimos que el\(z\) componente del par neto sea igual a cero (ya que todos los pares están en la\(z\) dirección), lo que nos permite determinar\(r_2\):\[\begin{aligned} \sum \tau_z = \tau_{1z} + \tau_{2z} + \tau_{gz} &=0\\ m_1 g r_1 -m_2 g r_2 -\left(\frac{L}{2}-d\right)Mg &=0\\ \therefore r_2 = \frac{1}{m_2} \left(m_1r_1-\left(\frac{L}{2}-d\right)M\right)\end{aligned}\] Tenga en cuenta que porque elegimos calcular los pares alrededor de un punto que va a través del fulcro, en este caso, no necesitábamos determinar el valor de la fuerza normal que obtuvimos de la Segunda Ley de Newton.

Discusión:

Este ejemplo resalta el hecho de que cuando un objeto está en equilibrio estático, podemos elegir un eje conveniente sobre el cual calcular los pares. En este caso, al calcular los pares sobre el fulcro, no fue necesario considerar el par de torsión a partir de la fuerza normal. Si hubiéramos elegido un punto diferente, entonces el par de torsión de la fuerza normal habría sido distinto de cero, y hubiéramos utilizado la Segunda Ley de Newton para expresar la fuerza normal en términos de las otras cantidades. Físicamente, si hubiéramos colocado el fulcro en el centro de la tabla\(d = L/2\), entonces habríamos encontrado eso\(m_1r_1 = m_2r_2\), la conocida ecuación para un equilibrio. Esta ecuación, por supuesto, viene de exigir que los pares de las fuerzas ejercidas por\(m_1\) y\(m_2\) sean iguales en magnitud y opuestos en dirección.

Equilibrio dinámico

Temas de revisión

Antes de continuar, es posible que desee revisar la Sección 5.6 sobre fuerzas inerciales.

Cuando un objeto está en equilibrio dinámico, su centro de masa se acelera, pero el objeto no gira cuando se ve desde su marco de referencia del centro de masa. Así, la suma de las fuerzas externas ejercidas sobre el objeto no es cero, mientras que el par externo neto ejercido sobre el objeto es cero, en el marco de referencia del centro de masa.

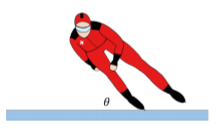
Considera, por ejemplo, un patinador de velocidad que recorre una pista circular o radio\(R\), y se inclina hacia el centro formando un ángulo\(\theta\) con el hielo, como se representa en la Figura\(\PageIndex{3}\). El centro de masa de la patinadora se está acelerando, porque está dando la vuelta a un círculo, por lo que la fuerza neta sobre la patinadora no es cero. Sin embargo, en el marco de referencia de la patinadora, la patinadora no está rotando; por lo tanto, se encuentra en equilibrio dinámico.

Figura\(\PageIndex{3}\): Una patinadora de velocidad que se inclina mientras da la vuelta a un círculo.

Las fuerzas sobre el patinador son:

1. \(\vec F_g\), su peso, ejercido en su centro de masa con magnitud,\(Mg\).
2. \(\vec N\), una fuerza normal, ejercida por el hielo hacia arriba sobre sus patines.
3. \(\vec f_s\), una fuerza de fricción estática, ejercida hacia el centro del círculo, por el hielo sobre sus patines.

Las fuerzas se ilustran en la Figura\(\PageIndex{4}\) junto con nuestra elección del sistema de coordenadas.

Figura\(\PageIndex{3}\).

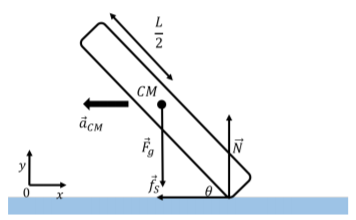
La suma de las fuerzas ejercidas sobre la patinadora debe ser hacia el centro del círculo e igual a la masa del patinador multiplicada por su aceleración centrípeta (que es la aceleración de su centro de masa,\(\vec a_{CM}\)). Los\(y\) componentes\(x\) y de la Segunda Ley de Newton están así dados por:\[\begin{aligned} \sum F_x &= -f_s = -ma_{CM}- m\frac{v^2}{R}\\ \sum F_y &= N-mg = 0\end{aligned}\]

Todas las fuerzas ejercidas sobre el patinador están en el\(xy\) plano, por lo que consideramos pares alrededor de un eje que es colineal con el\(z\) eje. Considera los pares alrededor de un eje a través del punto de contacto entre los patines y el hielo; hay un par neto en sentido antihorario debido al peso del patinador (el peso es la única fuerza que puede resultar en un par alrededor del punto de contacto con el hielo). Esperamos que la patinadora se vuelque, sin embargo, esto no debe ser un modelo correcto para la patinadora, ya que sabemos que es posible que ella se incline sin caer.

Consideremos, en cambio, la suma de los pares alrededor de un eje a través de su centro de masa. Si el patinador tiene una longitud\(L\) y el centro de masa está en medio del patinador, la suma de los pares alrededor del centro de masa viene dada por los pares de las fuerzas normales y la fuerza de fricción:\[\begin{aligned} \sum \tau = \tau_{Nz} + \tau_{f_sz} = \frac{L}{2}\cos\theta N - \frac{L}{2}\sin\theta f_s\end{aligned}\] Alrededor del centro de masa, los pares deben ser cero para que el patinador no pueda rotar, y esto daría una relación entre la fuerza de fricción estática y la fuerza normal.

¿Por qué obtenemos un modelo incorrecto cuando tomamos los pares sobre el punto de contacto entre el hielo y el patinador? Para determinar si el patinador está rotando, necesitamos estar en el mismo marco de referencia que el patinador. Sin embargo, el marco de referencia del patinador no es un marco de referencia inercial, ya que el patinador está acelerando. Todavía podemos modelar las fuerzas sobre el patinador en el marco de referencia no acelerante, siempre y cuando incluyamos la fuerza inercial,\(-m\vec a_{CM}\), en ese marco de referencia. En el marco de referencia del patinador, hay una fuerza inercial adicional\(-m\vec a_{CM}\), para que la suma de te fuerzas sea cero (en el marco de referencia del patinador, la suma de las fuerzas debe ser cero ya que el patinador no está acelerando en ese marco de referencia). La fuerza inercial adicional se ejerce en el centro de masa, como se ilustra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{3}\) como se ve en el marco acelerante de referencia del centro de masa.

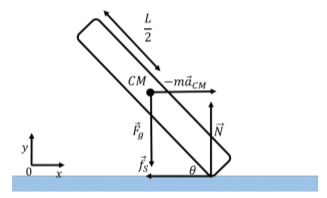
La razón por la que nuestro modelo funcionó al tomar los pares alrededor del centro de masa es que la fuerza inercial, ejercida en el centro de masa, no resulta en un par (ya que tiene un brazo de palanca de cero). Nuestro modelo estaba técnicamente equivocado, pero si tomamos los pares alrededor del centro de masa, entonces no necesitamos preocuparnos por la fuerza inercial. Si incluimos la fuerza inercial adicional, entonces podemos tomar los pares alrededor de cualquier punto, al igual que en el caso del equilibrio estático.