13.1: El movimiento de un sistema de masa-resorte

Como ejemplo de movimiento armónico simple, primero consideramos el movimiento de un bloque de masa\(m\) que puede deslizarse sin fricción a lo largo de una superficie horizontal. La masa está unida a un resorte con constante de resorte\(k\) que se une a una pared en el otro extremo. Introducimos un sistema de coordenadas unidimensional para describir la posición de la masa, de tal manera que el\(x\) eje es colineal con el movimiento, el origen se ubica donde el resorte está en reposo, y la dirección positiva corresponde a la extensión del resorte. Este “sistema de masa-resorte” se ilustra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un sistema de masa de resorte horizontal que oscila alrededor del origen con una amplitud\(A\).

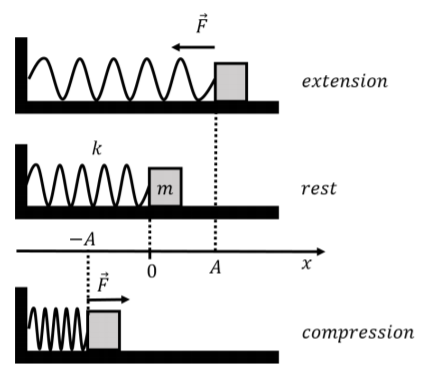
Suponemos que la fuerza ejercida por el resorte sobre la masa viene dada por la Ley de Hooke:\[\begin{aligned} \vec F = -kx \hat x\end{aligned}\] dónde\(x\) está la posición de la masa. Las únicas otras fuerzas ejercidas sobre la masa son su peso y la fuerza normal desde la superficie horizontal, que son iguales en magnitud y opuestas en dirección. Por lo tanto, la fuerza neta sobre la masa es la fuerza del resorte.

Como vimos en la Sección 8.4, si el resorte es comprimido (o extendido) por una distancia\(A\) relativa a la posición de reposo, y luego se libera la masa, la masa oscilará de un lado a otro entre\(x=\pm A\)¹, lo que se ilustra en la Figura\(\PageIndex{1}\). Llamamos a\(A\) la “amplitud del movimiento”. Cuando la masa está en\(x=\pm A\), su velocidad es cero, ya que estos puntos corresponden a la ubicación donde la masa “da la vuelta”.

Descripción usando energía

Podemos describir el movimiento de la masa usando energía, ya que la energía mecánica de la masa se conserva. En cualquier posición,\(x\), la energía mecánica,\(E\), de la masa tendrá un término de la energía potencial,\(U\), asociada a la fuerza del resorte, y la energía cinética,\(K\):\[\begin{aligned} E = U + K =\frac{1}{2}kx^2 + \frac{1}{2}mv^2\end{aligned}\] Podemos encontrar la energía mecánica, \(E\), evaluando la energía en uno de los puntos de inflexión. En estos puntos, la energía cinética de la masa es cero, entonces\(E=U(x=A)=1/2kA^2\). Entonces podemos escribir la expresión de energía mecánica como:

\[\frac{1}{2}kx^{2}+\frac{1}{2}mv^{2}=\frac{1}{2}kA^{2}\]

Así podemos conocer siempre la velocidad,\(v\), de la masa en cualquier posición,\(x\), si conocemos la amplitud\(A\):

\[\begin{aligned} v(x) = \sqrt{\frac{k(A^{2}-x^{2})}{m}}\end{aligned}\]

Ejercicio\(\PageIndex{1}\)

Si duplica la amplitud del movimiento de una masa unida a un resorte, su velocidad máxima será:

1. doble.
2. \(\sqrt 2\)veces mayores.
3. lo mismo.
4. reducido a la mitad.

Contestar

Cinemática del movimiento armónico simple

Podemos usar la Segunda Ley de Newton para obtener la posición\(x(t)\)\(v(t)\), velocidad y aceleración\(a(t)\), de la masa en función del tiempo. El\(x\) componente de la Segunda Ley de Newton para la masa adherida al resorte se puede escribir:\[\begin{aligned} \sum F_x = -kx = ma\end{aligned}\] Podemos escribir la aceleración en la Segunda Ley de Newton de manera más explícita como la segunda derivada de la posición,\(x(t)\), con respecto al tiempo. Si hacemos esto, podemos ver que la Segunda Ley de Newton para la masa unida al resorte es una ecuación diferencial para la función\(x(t)\) (la llamamos una “ecuación de movimiento”):

\[\begin{aligned} ma&=-kx \\ m\frac{d^{2}x}{dt^{2}}&=-kx \end{aligned}\]

\[\therefore \frac{d^{2}x}{dt^{2}}=-\frac{k}{m}x\]

Queremos encontrar la función de posición,\(x(t)\). La ecuación 13.1.2 nos dice que la segunda derivada de\(x(t)\) con respecto al tiempo debe ser igual al negativo de la\(x(t)\) función multiplicada por una constante,\(k/m\). Sin haber tomado un curso sobre ecuaciones diferenciales, podría no ser obvio cuál\(x(t)\) podría ser la función. Varias funciones equivalentes pueden satisfacer esta ecuación. Una opción posible, que presentamos aquí como suposición, es ²:

\[x(t)=A\cos(\omega t+\phi)\]

donde\(A\)\(\omega\),, y\(\phi\) son constantes que necesitamos determinar. Podemos tomar la derivada de segundo orden con respecto al tiempo de la función anterior para verificar que efectivamente “resuelve” la ecuación diferencial:\[\begin{aligned} x(t) &= A \cos(\omega t + \phi)\\ \frac{d}{dt}x(t) &= -A\omega\sin(\omega t + \phi)\\ \frac{d^2}{dt^2}x(t) &=\frac{d}{dt}\left( -A\omega\sin(\omega t + \phi)\right)= -A\omega^2\cos(\omega t + \phi)\\ \therefore \frac{d^2}{dt^2}x(t) &= - \omega^2 x(t)\end{aligned}\] La última ecuación tiene exactamente la misma forma que la Ecuación 13.1.2, que obtuvimos de la Segunda Ley de Newton, si definimos \(\omega\)como:

\[\omega = \sqrt{\frac{k}{m}}\]

Llamamos a\(\omega\) la “frecuencia angular” del sistema resorte-masa. Hemos encontrado que nuestra suposición para\(x(t)\) satisface la ecuación diferencial.

Ejercicio\(\PageIndex{2}\)

¿Cuál es la unidad SI para frecuencia angular?

1. \(\text{Hz}\)
2. \(\text{rad/s}\)
3. \(\text{N}^{1/2}\text{m}^{-1/2}\text{kg}^{-1/2}\)
4. Todo lo anterior

Contestar

Todo lo anterior

Pensamientos de Olivia

En el Capíto3, encontramos\(x(t)\), a partir de una función,\(a(t\)), mediante el uso de integración simple. Quizás se esté preguntando por qué no podemos hacer lo mismo con el fin de encontrar\(x(t)\) para el sistema masa-resorte. La diferencia es que, antes, la aceleración era una función del tiempo. Aquí, la aceleración es una función de\(x\). Esto significa que tenemos que usar un método diferente para resolver\(x(t)\), por lo que estamos haciendo estas “conjeturas” para resolver una ecuación diferencial.

Todavía necesitamos identificar cuáles son las constantes\(A\) y\(\phi\) tienen que ver con el movimiento de la masa. La constante\(A\) es el valor máximo que\(x(t)\) puede tomar (cuando el coseno es igual a 1). Esto corresponde a la amplitud del movimiento de la masa, que ya habíamos etiquetado,\(A\). La constante,\(\phi\), se llama la “fase” y depende de cuándo elegimos\(t=0\) ser. Supongamos que definimos el tiempo\(t=0\) para ser cuando la masa está en\(x=A\); en ese caso:\[\begin{aligned} x(t=0) &= A\\ A \cos(\omega t + \phi) &= A\\ A \cos(\omega (0) + \phi) &= A\\ \cos(\phi) &= 1\\ \therefore \phi = 0\end{aligned}\] Si\(t=0\) definimos ser cuando la masa está en\(x=A\), entonces la fase,\(\phi\), es cero. En general, el valor de\(\phi\) puede tomar cualquier valor entre\(-\pi\) y\(+\pi\)³ y, físicamente, corresponde a nuestra elección de cuándo\(t=0\) (es decir, la posición de la masa cuando elegimos\(t=0\)).

Dado que hemos determinado la posición en función del tiempo para la masa, su velocidad y aceleración en función del tiempo se encuentran fácilmente tomando las correspondientes derivadas del tiempo:\[\begin{aligned} x(t) &= A \cos(\omega t + \phi)\\ v(t) &= \frac{d}{dt}x(t) = -A\omega\sin(\omega t + \phi)\\ a(t)&= \frac{d}{dt}v(t) = -A\omega^2\cos(\omega t + \phi)\end{aligned}\]

Ejercicio\(\PageIndex{3}\)

¿Cuál es el valor de\(\phi\) if we choose \(t=0\) to be when the mass is at \(x=0\) and moving in the positive \(x\) direction?

1. \(\pi\)
2. \(-\pi\)
3. \(\pi/2\)
4. \(-\pi/2\)

Contestar

La posición de la masa es descrita por una función sinusoidal del tiempo; llamamos a este tipo de movimiento “movimiento armónico simple”. La posición y velocidad en función del tiempo para un sistema de masa de resorte con\(m=1\text{kg}\),\(k=4\text{N/m}\), se\(A=10\text{m}\) muestran en la Figura\(\PageIndex{2}\) para dos opciones diferentes de la fase,\(\phi=0\) y\(\phi=\pi/2\).

Figura\(\PageIndex{2}\): Posición y velocidad en función del tiempo para un sistema masa-resorte para dos valores diferentes de la fase,\(φ\).

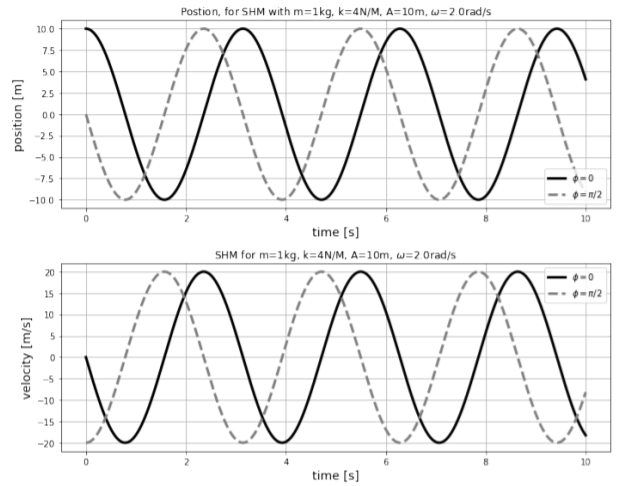
Podemos hacer algunas observaciones sobre la posición y velocidad ilustradas en la Figura\(\PageIndex{2}\):

• Cambiar la fase,\(\phi\), resulta en un desplazamiento horizontal de las funciones. Una fase positiva da como resultado un desplazamiento de las funciones hacia la izquierda.
• La velocidad más alta corresponde a una posición de\(x=0\) y la posición más grande\(x=\pm A\),, corresponde a una velocidad de cero.
• \(\phi = 0\)corresponde a la “condición inicial” en\(t=0\), donde está la posición de la masa\(x=A\) y su velocidad es\(v=0\).
• \(\phi = \pi/2\)corresponde a la “condición inicial” en\(t=0\), donde está la posición de la masa\(x=0\) y su velocidad está en la dirección negativa, y con amplitud máxima.
• La posición siempre está entre\(x=\pm A\), y la velocidad siempre está entre\(v=\pm A\omega\).

El movimiento de la primavera es claramente periódico. Si el periodo del movimiento es\(T\), entonces la posición de la masa en el momento\(t\) será la misma que su posición en\(t+T\). El periodo de la moción,\(T\), se encuentra fácilmente:

\[T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}\]

Y la frecuencia correspondiente viene dada por:

\[f=\frac{1}{T}=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\]

Ahora debería quedar claro por qué\(\omega\) se llama la frecuencia angular, ya que está relacionada con la frecuencia del movimiento.

Ejercicio\(\PageIndex{4}\)

Para duplicar el período de oscilación de un sistema de masa de resorte, puede

1. el doble de la relación de la masa sobre la constante de resorte.
2. cuadruplicar la masa.
3. reducir a la mitad la constante de primavera.
4. Todo lo anterior.

Contestar

Analogía con movimiento circular uniforme

Podemos hacer una analogía entre la descripción matemática del movimiento de un sistema de resorte-masa y la del movimiento circular uniforme. Considera una partícula que se mueve a lo largo de un círculo de radio\(A\), con velocidad angular constante\(\omega\), como se ilustra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Movimiento circular uniforme de una partícula a lo largo de un círculo de radio\(A\) con velocidad angular constante\(\omega\).

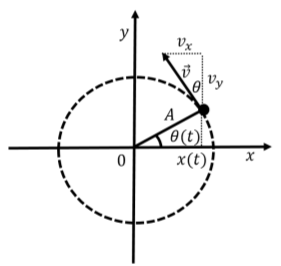
La posición angular,\(\theta(t)\), de la partícula viene dada por:\[\begin{aligned} \theta(t) = \theta_0 + \omega t\end{aligned}\] si la partícula se ubicó en una posición angular\(\theta_0\) en\(t=0\) (\(\theta_0=0\)en la Figura\(\PageIndex{3}\)). La\(x\) coordenada de la partícula viene dada por:\[\begin{aligned} x(t) = A\cos(\theta(t)) = A\cos(\theta_0 + \omega t)\end{aligned}\]

Podemos ver que la\(x\) coordenada de la partícula tiene la misma forma funcional que la posición para el movimiento armónico simple. Lo mismo es cierto para la velocidad de la partícula. La magnitud de la velocidad de la partícula viene dada por:\[\begin{aligned} v = \omega r = \omega A\end{aligned}\] donde\(r=A\) está el radio del círculo. El\(x\) componente de la velocidad de la partícula se encuentra fácilmente a partir de la figura y viene dado por:\[\begin{aligned} v_x(t) = -v\sin(\theta(t)) = -\omega A\sin(\theta_0 + \omega t)\end{aligned}\] Podemos visualizar el movimiento armónico simple como si fuera la proyección sobre el\(x\) eje de movimiento circular uniforme con velocidad angular\(\omega\) alrededor de un círculo con radio\(A\). La fase\(\phi\) corresponde a la posición angular de la partícula alrededor del círculo,\(\theta_0\), en el momento\(t=0\). Cuando la partícula cruza el\(y\) eje (\(x=0\)), su velocidad está en la\(x\) dirección, por lo que el\(x\) componente de la velocidad es máxima. Cuando la partícula cruza el\(x\) eje (\(x=\pm A\)), el\(x\) componente de la velocidad es cero.

Pensamientos de Olivia

Aquí hay una visualización del movimiento circular uniforme proyectado sobre el\(x\) eje:

Figura\(\PageIndex{4}\): Proyectar el movimiento de una bola alrededor de un círculo sobre el\(x\) eje.

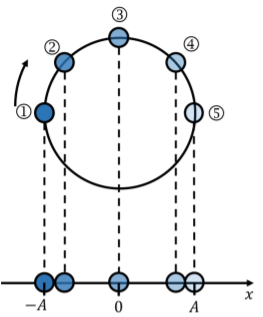
La figura\(\PageIndex{4}\) muestra una bola moviéndose a una velocidad constante alrededor de un círculo de radio\(A\). En este diagrama, he tomado instantáneas del movimiento de la pelota a intervalos de tiempo regulares a medida que la pelota se mueve de la Posición 1 a la Posición 5. Dado que la velocidad es constante, las bolas están uniformemente espaciadas alrededor del círculo. En la parte inferior de la figura, se puede ver cómo se vería si solo consideráramos el movimiento en la\(x\) dirección (esta es la proyección del movimiento sobre el\(x\) eje). También podrías pensar en esto como cómo se vería la moción si miraras hacia arriba el círculo desde abajo. Como se puede ver, esta proyección se parece mucho al movimiento de una masa sobre un resorte. El movimiento de la pelota está restringido entre\(-A\) y\(+A\) (los puntos de inflexión), y la velocidad de la bola, en la\(x\) dirección, será mayor cuando\(x=0\). Hay toneladas de videos en línea que muestran animaciones de este concepto, solo busca “SHM como una proyección de movimiento circular” y obtendrás muchas formas diferentes de visualizar esto.

Notas al pie

1. Siempre y cuando no haya fricción para reducir la energía mecánica de la masa.

2. Otras posibles conjeturas que funcionan son\(A \sin(\omega t + \phi)\), y\(x(t) = A\cos(\omega t) + B\sin(\omega t)\).

3. El argumento a la función coseno está en radianes, ya que la frecuencia angular suele definirse en radianes por segundo. El valor de\(\phi\) está restringido a estar dentro de ese rango, ya que la función coseno es periódica con un punto\(2\pi\).