15.3: Hidrodinámica
- Page ID
- 129103
En las secciones anteriores desarrollamos modelos “hidrostáticos” para fluidos cuando esos fluidos están en reposo (en algún marco de referencia inercial). En esta sección, desarrollamos modelos “hidrodinámicos” para discutir lo que sucede cuando fluyen los fluidos. Vamos a restringir nuestros modelos a fluidos que fluyan de manera “laminar”, en lugar de una manera “turbulenta”.
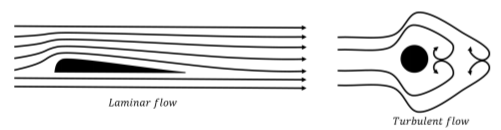
El flujo laminar es el flujo de un fluido cuando cada partícula en el fluido sigue una trayectoria que puede ser representada por una línea (una “línea aerodinámica”). El flujo turbulento es el flujo de un fluido donde las partículas pueden seguir caminos bastante complejos, generalmente involucrando “corrientes parásitas” (pequeños remolinos). Los dos tipos de flujo se ilustran en la Figura\(\PageIndex{1}\).
Continuidad del flujo
Considere el flujo laminar de un fluido a través de una tubería cuya área de sección transversal se estrecha de\(A_{1}\) a\(A_{2}\) en la dirección del flujo, como se ilustra en la Figura\(\PageIndex{2}\).
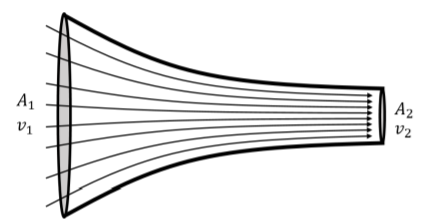
Las partículas que componen el fluido tienen una velocidad\(v_{1}\) en el extremo ancho de la tubería y velocidad\(v_{2}\) en el extremo estrecho. La ecuación de continuidad se basa en la premisa de que el fluido que ingresa a la tubería debe salir de la tubería, ya que no hay otro lugar para que vaya el fluido. Es decir, si durante un periodo de tiempo,\(∆t\), una masa\(∆m\), de fluido entra en el extremo ancho de la tubería, entonces durante ese mismo periodo de tiempo, la misma masa de fluido debe salir del extremo estrecho de la tubería.
Durante un periodo de tiempo,\(∆t\), el fluido en el extremo ancho de la tubería recorrerá una distancia\(l_{1} = v_{1}∆t\). Así, un volumen de fluido,\(∆V_{1}\), entrará en el extremo ancho de la tubería:
\[\begin{aligned} \Delta V_{1}=A_{1}l_{1}=A_{1}v_{1}\Delta t \end{aligned}\]
De igual manera, durante ese periodo de tiempo, un volumen\(∆V_{2}\) saldrá del extremo estrecho de la tubería:
\[\begin{aligned} \Delta V_{2}=A_{2}l_{2}=A_{2}v_{2}\Delta t \end{aligned}\]
Si el fluido es compresible, su densidad puede cambiar. Dejar\(ρ_{1}\) ser la densidad del fluido en el extremo ancho de la tubería y\(ρ_{2}\) ser la densidad del fluido en el extremo estrecho. La masa de fluido,\(∆m\), que entra en el extremo ancho de la tubería viene dada por:
\[\begin{aligned} \Delta m = \rho _{1}\Delta V_{1}=\rho _{1}A_{1}v_{1}\Delta t \end{aligned}\]
La masa de fluido que sale del extremo estrecho de la tubería viene dada por:
\[\begin{aligned} \Delta m = \rho _{2}\Delta V_{2} = \rho _{2}A_{2}v_{2}\Delta t\end{aligned}\]
La masa de fluido que ingresa al extremo ancho de la tubería debe ser igual a la masa que sale del extremo estrecho de la tubería:
\[\begin{aligned} \rho _{1}A_{1}v_{1}\Delta t = \rho _{2}A_{2}v_{2}\Delta t \end{aligned}\]
Conducir a la ecuación de continuidad:
\[\rho _{1}A_{1}v_{1}=\rho _{2}A_{2}v_{2}\]
La cantidad\(ρAv\) tiene dimensiones de masa por tiempo, y corresponde a la masa de fluido que pasa por una sección transversal\(A\) por unidad de tiempo.
Si el fluido es incompresible, como lo son la mayoría de los líquidos, entonces la densidad es la misma en ambos lados de la tubería, y la ecuación se simplifica para:
\[A_{1}v_{1}=A_{2}v_{2}\qquad\text{(Incompressible fluid)}\]
Para un líquido, podemos definir el “flujo volumétrico”,\(Q\), como:
\[\begin{aligned} Q=Av \end{aligned}\]
donde\(A\) es el área de la sección transversal de la superficie a través de la cual fluye un fluido con velocidad\(v\),, 1. \(Q\)tiene la dimensión de volumen por tiempo, y corresponde al volumen de fluido que pasa por la sección transversal\(A\) por unidad de tiempo. Para un fluido incompresible, la ecuación de continuidad es así equivalente a afirmar que el flujo volumétrico\(Q\),, del fluido es una constante.
Ejercicio\(\PageIndex{1}\)
Cuando el agua sale de tu grifo, observas que el chorro de agua se estrecha a medida que el agua se mueve hacia abajo, como se muestra en la Figura\(\PageIndex{3}\). ¿Por qué es esto?
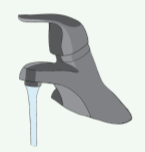
- La presión atmosférica aumenta a medida que las aguas se mueven hacia abajo, por lo que la corriente de agua se comprime cada vez más.
- A medida que el agua se acelera debido a la gravedad, el área de la sección transversal del agua que fluye debe reducirse para preservar un caudal constante.
- Contestar
Ejemplo\(\PageIndex{1}\)
Tu manguera de jardín tiene un diámetro de\(D = 2\text{ cm}\). ¿Qué tan rápido debe salir el agua de la manguera si va a llenar un\(5\text{ l}\) cubo en un minuto?
Solución:
Necesitamos que el caudal volumétrico de la manguera sea\(Q = 5\text{ l/min}\). Podemos convertir esto en unidades SI:
\[\begin{aligned} Q=(5\text{l/min})\left( \frac{1}{1000}\text{m}^{3}\text{/l} \right)\left( \frac{1}{60}\text{min/s} \right)=\frac{5}{6\times 10^{4}}\text{m}^{3}\text{/s} = 8.3\times 10^{-5}\text{m}^{3}\text{/s} \end{aligned}\]
Dado que conocemos el área de la manguera, podemos determinar la velocidad del agua para lograr el caudal dado:
\[\begin{aligned} Q&=Av=\pi \left(\frac{D}{2} \right)^{2}v \\ \therefore v&=\frac{Q}{\pi \left( \frac{D}{2} \right)^{2}}=\frac{(8.3\times 10^{-5}\text{m}^{3}\text{/s})}{\pi (0.01\text{m})^{2}}=0.265\text{m/s} \end{aligned}\]
Principio de Bernoulli
En esta sección, examinamos cómo la presión y la velocidad de un fluido cambian a medida que fluye el fluido. Nos limitaremos a discutir el flujo laminar de un fluido incompresible sin fricción. Bernoulli fue el primero en describir cuantitativamente el flujo de fluidos incompresibles, y mostraremos en esta sección cómo derivar “Principio de Bernoulli”.
Considerar el flujo laminar de un fluido incompresible a través de una tubería que cambia de altura, de\(y_{1}\) a\(y_{2}\), así como de área de sección transversal, de\(A_{1}\) a\(A_{2}\), como se muestra en la Figura\(\PageIndex{4}\). La figura muestra un elemento de fluido, en azul, a medida que se mueve a través de la tubería. El panel superior corresponde a la ubicación del elemento fluido en el momento\(t = 0\), mientras que el panel inferior muestra la ubicación del elemento de fluido en el momento\(t = ∆t\).
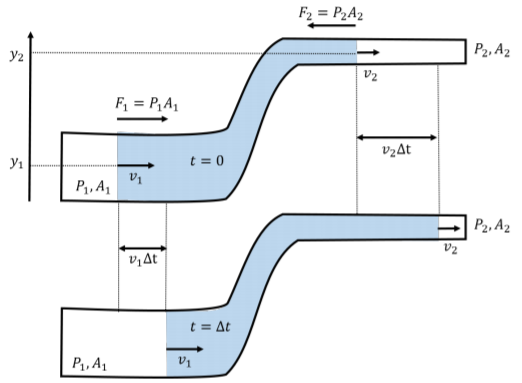
Para modelar cómo se mueve el fluido a través de esta tubería, podemos usar la energía y el Teorema de Trabajo-Energía. Comenzamos considerando la cantidad de trabajo realizado en el elemento de fluido a medida que se mueve desde la posición en el panel superior hasta la posición en el panel inferior.
El fluido que está a la izquierda del elemento de fluido ejerce una presión,\(P_{1}\), sobre el elemento fluido que conduce a una fuerza neta,\(\vec F_{1}\), hacia la derecha. De igual manera, el fluido a la derecha del elemento de fluido ejerce una fuerza neta\(\vec F_{2}\) en sentido contrario, debido a la presión\(P_{2}\) en ese lado del elemento fluido.
En un periodo de tiempo,\(∆t\), la parte izquierda del elemento fluido se moverá una distancia\(l_{1} = v_{1}∆t\), mientras que la parte derecha del elemento fluido se moverá una distancia\(l_{2} = v_{2}∆t\). Podemos calcular el trabajo realizado por cada fuerza, definiendo el trabajo positivo para estar en la dirección del movimiento:
\[\begin{aligned} W_{1}&=F_{1}l_{1}=(P_{1}A_{1})(v_{1}\Delta t) \\ W_{2} &=-F_{2}l_{2}=-(P_{2}A_{2})(v_{2}\Delta t) \end{aligned}\]
La gravedad también hará trabajo (negativo) en el fluido a medida que cambia de altura. En un periodo de tiempo,\(∆t\), una masa de fluido,\(∆m\), se moverá de una posición\(y = y_{1}\) a otra\(y = y_{2}\). La masa de fluido que cambia de altura viene dada por la parte del fluido que se mueve una distancia,\(l_{1}\), en el lado derecho de la tubería:
\[\begin{aligned} \Delta m = V_{1}\rho = A_{1}l_{1}\rho = A_{1}v_{1}\Delta t\rho \end{aligned}\]
Debido a la ecuación de continuidad, esto también es igual a la masa de fluido que se mueve una distancia,\(l_{2}\), en el lado izquierdo de la tubería:
\[\begin{aligned} \Delta m = V_{2}\rho = A_{2}l_{2}\rho = A_{2}v_{2}\Delta t\rho \end{aligned}\]
ya que\(A_{1}v_{1}=A_{2}v_{2}\).
La fuerza de gravedad hará así un trabajo negativo en ese elemento de masa:
\[\begin{aligned} W_{g}=-\Delta mg(y_{2}-y_{1})=-(A_{1}v_{1}\Delta t\rho)g(y_{2}-y_{1}) \end{aligned}\]
El trabajo neto realizado en el elemento de fluido a lo largo del tiempo\(∆t\) es así:
\[\begin{aligned} W^{net}=W_{1}+W_{2}+W_{g}=P_{1}A_{1}v_{1}\Delta t-P_{2}A_{2}v_{2}\Delta t - A_{1}v_{1}\Delta t \rho g(y_{2}-y_{1}) \end{aligned}\]
Tenga en cuenta que, debido a la ecuación de continuidad\(A_{1}v_{1} = A_{2}v_{2}\),, podemos facturar a\(A_{1}v_{1}\) de cada término:
\[\begin{aligned} W^{net}=A_{1}v_{1}\Delta t(P_{1}-P_{2}-\rho g(y_{2}-y_{1})) \end{aligned}\]
El trabajo neto realizado en el fluido debe ser igual al cambio en la energía cinética\(∆K\),, del elemento de masa\(∆m\),, de un extremo de la tubería al otro:
\[\begin{aligned} \begin{aligned} \Delta K&=\frac{1}{2}\Delta mv_{2}^{2} - \frac{1}{2}\Delta mv_{1}^{2} \\ &=\frac{1}{2}(A_{1}v_{1}\Delta t\rho )(v_{2}^{2}-v_{1}^{2}) \end{aligned} \end{aligned}\]
Utilizando el Teorema de Trabajo y Energía, tenemos:
\[\begin{aligned} W^{net}&=\Delta K \\ A_{1}v_{1}\Delta t\left(P_{1} - P_{2}-\rho g(y_{2}-y_{1})\right)&=\frac{1}{2}(A_{1}v_{1}\Delta t\rho )(v_{2}^{2}-v_{1}^{2}) \\ P_{1}-P_{2}-\rho g(y_{2}-y_{1})&=\frac{1}{2}\rho v_{2}^{2}-\frac{1}{2}\rho v_{1}^{2} \end{aligned}\]
Podemos reorganizar esto para que todas las cantidades para cada lado de la tubería estén en el mismo lado de la ecuación:
\[\begin{aligned} P_{1}+\frac{1}{2}\rho v_{1}^{2} +\rho gy_{1}=P_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho gy_{2} \end{aligned}\]
Dado que las ubicaciones 1 y 2 que elegimos son arbitrarias, podemos afirmar que, para el flujo laminar incompresible, la siguiente cantidad evaluada en cualquier posición es una constante:
\[P+\frac{1}{2}\rho v^{2}+\rho gy = \text{constant}\]
Esta afirmación es lo que llamamos la Ecuación de Bernoulli, y equivale a la conservación de energía para el fluido. Si el fluido no está fluyendo\((v_{1} = v_{2} = 0)\), entonces esto equivale a la declaración de equilibrio hidrostático que derivamos en la Ecuación 15.1.1:
\[\begin{aligned} P_{1}+\rho gy_{1}&=P_{2}+\rho gy_{2} \\ \therefore P_{2}-P_{1}=-\rho g(y_{2}-y_{1}) \end{aligned}\]
Si el flujo del fluido está a una altura constante\((y_{2} = y_{1})\), entonces la ecuación de Bernoulli se puede escribir como:
\[\begin{aligned} P_{1}+\frac{1}{2}\rho v_{1}^{2}=P_{2}+\frac{1}{2}\rho v_{2}^{2} \end{aligned}\]
Si un fluido fluye a altura constante tal que\(v_{2} > v_{1}\) (como en la Figura\(\PageIndex{2}\)), entonces\(P_{2} < P_{1}\); es decir, la presión en el fluido es menor si el fluido fluye más rápido. Tenga en cuenta que\(P\) es la presión dentro del fluido y no está relacionada con la fuerza que ejercería el fluido si chocara con un objeto. Tiene sentido que el fluido tenga una menor presión donde se mueve más rápido, debido a que la fuerza neta ejercida sobre el fluido está relacionada con la diferencia de presión a cada lado del fluido. El fluido se acelerará en la dirección donde la presión disminuye, por lo que se irá moviendo más rápido cuando se encuentre en una región de baja presión.
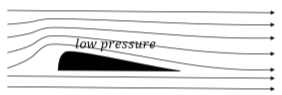
El principio de Bernoulli se puede utilizar para describir muchos fenómenos. Por ejemplo, un ala de un avión (técnicamente, un “perfil aerodinámico”) crea sustentación porque la presión del aire por encima del ala es menor que la presión sobre el ala. Esto se ilustra en la Figura\(\PageIndex{5}\), que muestra que el flujo laminar del aire crea un área de baja presión por encima del ala. A medida que las líneas de corriente de aire se encuentran con el ala, las que están por encima del ala se comprimen juntas, lo que lleva a una velocidad más rápida del aire por encima del ala (ecuación de continuidad). La diferencia resultante en la presión del aire por encima y por debajo del ala da como resultado una fuerza neta hacia arriba en el ala.
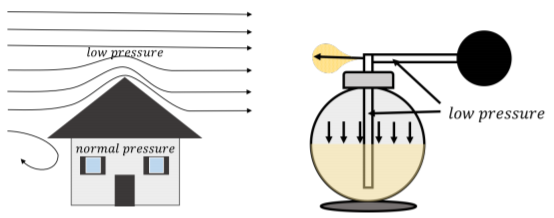
El principio de Bernoulli también describe por qué el techo se puede levantar de una casa con vientos fuertes (Figura\(\PageIndex{6}\), panel izquierdo). No es la fuerza del viento contra el techo lo que sopla el techo de una casa; es la diferencia en la presión del aire en la casa (normal) y la presión sobre el techo (baja, debido al viento que fluye), lo que da como resultado una fuerza neta hacia arriba en el techo. El principio de Bernoulli también se utiliza para construir atomizadores que permiten rociar líquido en una botella (Figura\(\PageIndex{6}\), panel derecho). Por ejemplo, los frascos de perfume a menudo tienen una bombilla conectada a un tubo/boquilla. Al apretar la bombilla, hace que el aire en el tubo fluya rápidamente, creando una baja presión en el segmento vertical de la boquilla. El líquido es forzado hacia arriba por la presión en la botella; una vez que el líquido llega al aire que fluye rápido, se rocía junto con el aire.
Ejercicio\(\PageIndex{2}\)
Cuando un tren de alta velocidad viaja a velocidad constante, ¿hay una fuerza neta en las ventanas por la presión del aire?
- No, dado que las ventanas están estacionarias con relación al tren, no hay fuerza neta sobre ellas por la presión del aire.
- Sí, hay una fuerza neta hacia afuera en las ventanas por la presión del aire.
- Sí, hay una fuerza neta hacia adentro en las ventanas por la presión del aire.
- Contestar
Los siguientes ejemplos ilustran cómo aplicar el principio de Bernoulli.
Ejemplo\(\PageIndex{2}\)
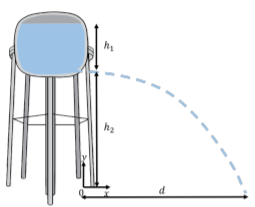
Se construye una torre de agua de manera que el fondo del tanque de agua esté a una altura\(h_{2}\) por encima del suelo, como se ilustra en la Figura\(\PageIndex{7}\). El agua en el tanque está a una altura\(h_{1}\) desde el fondo del tanque. Una fuga de un agujero se encuentra en la base del tanque (el agua fluye horizontalmente fuera del agujero). ¿Cuál es la distancia horizontal\(d\),, desde el fondo de la torre hasta donde el agua de la fuga golpea el suelo? Supongamos que el nivel del agua en el tanque es constante y que la presión atmosférica no cambia apreciablemente a lo largo de la altura de la torre.
Solución:
La presión en el tanque de agua lleva al agua que sale del fondo del tanque con una velocidad horizontal de magnitud,\(v\). Esa agua sufre entonces un movimiento de proyectil en su camino hacia el suelo. Primero podemos determinar la velocidad del agua que sale del tanque y luego usar la cinemática para el movimiento del proyectil para modelar la distancia,\(d\).
Modelamos el flujo del agua utilizando un sistema de coordenadas bidimensional con un\(x\) eje horizontal (positivo a la derecha) y un\(y\) eje vertical (positivo hacia arriba). Colocamos el origen en el fondo de la torre de agua, en el suelo, debajo del agujero, como se muestra en la Figura\(\PageIndex{7}\).
En la parte superior del tanque, a una altura\(y = h_{1} + h_{2}\), el agua tiene una velocidad de cero y está a presión atmosférica,\(P_{0}\). A la salida del agujero en el fondo del tanque, a una altura\(y = h_{2}\), el agua tiene una velocidad\(v_{2}\) y también se encuentra a presión atmosférica. Usando la ecuación de Bernoulli en la parte superior (1) e inferior (2) del tanque, tenemos:
\[\begin{aligned} P_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho gy_{1}&=P_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho gy_{2} \\ P_{0} +(0) +\rho g(h_{1}+h_{2})&=P_{0}+\frac{1}{2}\rho v^{2}+\rho gh_{2} \\ \therefore v_{2}&=\sqrt{2gh_{1}} \end{aligned}\]
que es exactamente la velocidad que\(h_{1}\) tendría cualquier objeto que cayera a una distancia.
Usando la cinemática, podemos encontrar el tiempo que tardaría el agua en caer una distancia\(h_{2}\) (donde la velocidad del agua es horizontal a medida que sale del tanque):
\[\begin{aligned} h_{2}&=\frac{1}{2}gt^{2} \\ \therefore t&=\sqrt{\frac{2h_{2}}{g}} \end{aligned}\]
Así pues, la distancia\(d\) recorrida por el agua viene dada por:
\[\begin{aligned} d=v_{2}t=\sqrt{2gh_{1}}\sqrt{\frac{2h_{2}}{g}}=\sqrt{4h_{1}h_{2}} \end{aligned}\]
Discusión:
Encontramos que el agua que sale del fondo del tanque, cuando hay una altura,\(h_{1}\), de agua por encima de ella proporcionando presión, tendrá la misma velocidad que la de una partícula que ha caído una distancia,\(h_{1}\). Esto se debe a que no hay diferencia neta de presión entre la parte superior del tanque de agua y donde el agua ha salido del agujero, por lo que la gravedad es la única fuerza que trabaja en el agua. La gravedad hará trabajo a la misma velocidad en partículas de agua que en cualquier otra partícula, por lo que la velocidad de las partículas de agua en el fondo del tanque es la misma que si hubieran caído una distancia,\(h_{1}\). Nuevamente, una vez que las partículas de agua caen por el aire, la gravedad es la única fuerza neta que se ejerce sobre esas partículas, por lo que sufren movimiento de proyectil, tal como lo haría cualquier otra partícula.
Ejemplo\(\PageIndex{3}\)
Mides que el agua sale del grifo de tu cocina a un ritmo de\(6\text{ l/min}\). El grifo tiene un diámetro de\(2\text{ cm}\). ¿A qué velocidad fluirá el agua de su grifo del sótano, que tiene un diámetro de\(1\text{ cm}\) y se encuentra a una altura,\(h=\text{ 3 m}\), debajo del grifo de su cocina? Supongamos que la presión atmosférica\(P_{0}\),, no cambia apreciablemente entre su cocina y sótano.
Solución:
El agua sale del grifo de la cocina a una velocidad,\(v_{1}\), donde la presión es atmosférica. Si el área del grifo de la cocina es\(A_{1}\) podemos determinar la velocidad,\(v_{1}\), a partir del caudal dado,\(Q_{1} = 6 \text{l/min} = 1 × 10^{−4} \text{m}^{3}\text{/s}\):
\[\begin{aligned} Q_{1}&=A_{1}v_{1} \\ v_{1}&=\frac{Q_{1}}{A_{1}}=\frac{(1\times 10^{-4}\text{m}^{3}\text{/s})}{\pi (0.01\text{cm})^{2}}=0.318\text{m/s} \end{aligned}\]
El agua saldrá del grifo del sótano con una velocidad,\(v_{2}\), donde la presión también es atmosférica,\(P_{0}\). Podemos usar la ecuación de Bernoulli para relacionar el flujo que sale del grifo del sótano (2) con el del grifo de la cocina (1). Elegimos el\(y\) eje de un sistema de coordenadas verticales de tal manera que el sótano se ubica en\(y_{2} = 0\) y el grifo de la cocina se ubica en\(y_{1} = 3\text{ m}\):
\[\begin{aligned} P_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho gy_{1}&=P_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho gy_{2} \\ P_{0}+\frac{1}{2}\rho v_{1}^{2}+\rho gy_{1}&=P_{0}+\frac{1}{2}\rho v_{2}^{2} \\ \frac{1}{2}v_{1}^{2}+gy_{1}&=\frac{1}{2}v_{2}^{2} \\ \therefore v_{2}&=\sqrt{v_{1}^{2}+2gy_{1}} \\ &=\sqrt{(0.318\text{m/s})^{2}+2(9.8\text{m/s}^{2})(3\text{m})} = 7.67\text{m/s} \end{aligned}\]
El caudal correspondiente en el grifo del sótano será:
\[\begin{aligned}Q_{2}=A_{2}v_{2}=\pi(0.005\text{m})^{2}(7.67\text{m/s})=6.03\times 10^{-4}\text{m}^{3}\text{/s}=36.171\text{/min}\end{aligned}\]
Discusión:
Encontramos que el caudal que sale del grifo del sótano es seis veces mayor que en el grifo de la cocina. La velocidad del agua que sale del grifo del sótano es más que\(20\) veces la velocidad del agua en el grifo de la cocina. Si bien es cierto que uno obtiene mejor presión de agua de un grifo que es más bajo en el edificio, este cambio en el flujo es poco realista alto, y este es un modelo pobre para el flujo de agua en las tuberías de su casa.
Puedes verificar fácilmente que la velocidad del agua en diferentes niveles de tu casa no varíe en un factor cercano\(20\) para un\(3\text{ m}\) cambio de altura (podrías comparar el caudal para dos grifos con el mismo diámetro). Esto se debe a que nuestro modelo descuida el efecto de la fricción a medida que el agua fluye en las tuberías; en realidad, hay mucha mayor presión en las tuberías que esa por la gravedad, así como un gradiente en la presión en sus tuberías, que llevará a que los caudales sean similares en su cocina y sótano.
Viscosidad
Hasta el momento, hemos asumido que los fluidos fluyen sin fricción. En realidad, las partículas que se mueven en un fluido ejercen fricción interna unas sobre otras llamadas “viscosidad”. Esto se puede modelar como la fricción entre diferentes capas de fluido en un flujo laminar. Por ejemplo, puede notar que el agua que fluye en un río ancho fluye mucho más rápido en medio del río que cerca de las orillas del río, donde el agua es casi estacionaria, como se muestra en la Figura\(\PageIndex{8}\).
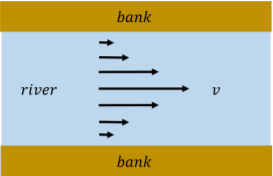
Se puede modelar las orillas del río como ejerciendo una fuerza de fricción sobre la capa de agua que está en contacto con las orillas. Esa capa ejerce entonces una fuerza de fricción sobre la siguiente capa más cercana al centro del río, y así sucesivamente.
Se puede definir un coeficiente de viscosidad\(η\), basado en medir la fuerza requerida para tirar de una placa más allá de otra placa cuando hay un fluido entre las placas. Considera dos placas que tienen un área,\(A\), que están a una\(l\) distancia entre sí, y contienen el fluido de interés entre ellas, como se ilustra en la Figura\(\PageIndex{9}\).
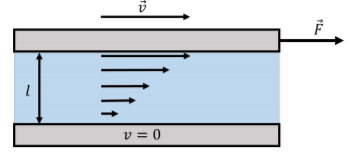
La viscosidad del fluido se define en base a la fuerza que se requiere para tirar de la placa superior mientras la placa inferior permanece inmóvil. La capa de fluido directamente debajo de la placa móvil se moverá con la placa a una velocidad\(v\), mientras que la capa de fluido inmediatamente en contacto la placa estacionaria también estará estacionaria. Mover una placa conducirá así a un gradiente (un cambio) en la velocidad del fluido en función de la posición entre las dos placas. La magnitud de la fuerza\(\vec F\), requerida para mover una placa con velocidad,\(v\), se determinó empíricamente como proporcional al área de las placas,\(A\), y la velocidad\(v\), siendo inversamente proporcional a la distancia,\(l\), entre las dos placas:
\[\begin{aligned} F ∝ A\frac{v}{l} \end{aligned}\]
La constante de proporcionalidad se define como la viscosidad\(η\),, del fluido:
\[F=ηA\frac{v}{l}\]
Si la viscosidad del fluido es cero, entonces no se requiere fuerza para tirar de la placa. Cuanto más viscoso es el fluido, más difícil es tirar de la placa superior. Puedes experimentar con esto comparando la fuerza requerida para mover un pequeño trozo de papel por la parte superior de un charco de agua y por la parte superior de la miel.
La presencia de viscosidad significa que cualquier fluido que fluya perderá energía mecánica debido a la fricción interna (que calentará el fluido). Por lo tanto, la ecuación de Bernoulli no es correcta si el fluido tiene viscosidad, ya que un fluido no puede fluir a través de una tubería horizontal sin un cambio de presión para superar las pérdidas debidas a la fricción.
Flujo de Poiseuille
Para el flujo de un fluido viscoso incompresible a través de una tubería, se puede postular que el caudal,\(Q\), es proporcional al cambio de presión,\(∆P\), a través de la tubería:
\[\begin{aligned} Q ∝ ∆P \end{aligned}\]
donde\(∆P\) se toma como la diferencia positiva entre la presión en cualquiera de los extremos de la tubería. El fluido fluye de alta presión a baja presión. Podemos introducir una constante de proporcionalidad,\(R\), para ser la “resistencia de la tubería”, para que podamos escribir:
\[\begin{aligned} Q=\frac{\Delta P}{R} \end{aligned}\]
donde escribimos la constante de proporcionalidad como\(1/R\), de manera que un mayor valor de\(R\) corresponde a una tubería con una mayor resistencia al flujo. Es decir, para una diferencia de presión dada, a medida que se aumenta la resistencia de la tubería, se disminuye el caudal a través de esa tubería. La relación anterior puede ser utilizada para determinar empíricamente la resistencia de una tubería.
El flujo a través de una tubería con una resistencia dada será cero si no hay gradiente de presión en el fluido a lo largo de la tubería. Por el contrario, si no hay flujo de fluido en la tubería, la presión es la misma en todas partes de la tubería. Por lo tanto, también podemos ver una caída de presión en una tubería para ser el resultado del flujo de líquido a través de la tubería. La presión no puede caer a través de una tubería horizontal si no hay flujo.
Cuando cierras el grifo de tu cocina, la presión dentro del grifo está cerca de la presión en la línea principal de agua que abastece tu casa. Tan pronto como abra el grifo y permita que el agua fluya, la presión en su grifo cae a la presión atmosférica, y el gradiente de presión resultante del suministro principal obliga al agua a fluir fuera del grifo. Si intentas tapar el grifo de tu cocina con el pulgar y detener el flujo de agua, necesitarás ejercer una fuerza lo suficientemente grande como para superar la presión que existe en el suministro principal de agua. Encontrarás que es prácticamente imposible detener el flujo de agua con el pulgar, ya que la presión en el suministro principal necesita ser lo suficientemente alta como para superar la resistencia de las tuberías y aún así resultar en un flujo de agua utilizable.
Poiseuille desarrolló primero un modelo para el flujo laminar de un líquido a través de una tubería cilíndrica horizontal uniforme de longitud\(L\), con una sección transversal circular con radio\(r\). Encontró que la resistencia de una tubería de este tipo a un fluido de viscosidad,\(η\), viene dada por:
\[\begin{aligned} R=\frac{8ηL}{\pi r^{4}} \end{aligned}\]
Esto tiene cierto sentido intuitivo, ya que esperamos más resistencia (más impedancia al flujo), si la tubería es más larga y si el fluido es más viscoso (la resistencia es cero si no hay viscosidad). Además, esperamos menos resistencia si la tubería tiene un radio mayor. La resistencia encontrada por Poiseuille baja como la cuarta potencia del radio. Así, una tubería que sea el doble de ancha tendrá un flujo volumétrico que es\(2^{4} = 16\) veces mayor debido a la resistencia reducida.
El caudal laminar,\(Q\), de un fluido viscoso a través de una tubería de longitud\(L\) y radio\(R\), cuando hay una diferencia de presión\(∆P\), viene dado por:
\[Q=\frac{\pi r^{4}}{8ηL}\Delta P\]
Esto se suele denominar “Ecuación de Poiseuille”.
Ejercicio\(\PageIndex{3}\)
¿El caudal de agua que sale de una manguera de jardín depende de la longitud de la manguera?
- No, ya que el volumen de agua que ingresa a la manguera también debe salir de la manguera, no importa cuánto tiempo esté la manguera.
- Sí, la resistencia de la manguera depende de su longitud, por lo que la caída de presión a través de la manguera cambiará y también lo hará el caudal.
- Contestar
Ejemplo\(\PageIndex{4}\)
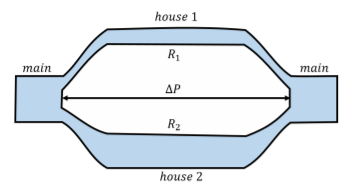
Estás modelando el flujo de agua para una ciudad. Dos casas están conectadas en paralelo al suministro principal de agua, de manera que el agua del suministro principal desemboca en la casa 1 o casa 2, y los flujos que salen de cada casa luego se unen nuevamente en el suministro principal. La diferencia de presión,\(∆P\), entre el punto de entrada y salida del agua es la misma para cada casa, y cada casa puede modelarse como teniendo una resistencia neta,\(R_{1}\) o\(R_{2}\), al flujo de agua, como se ilustra en la Figura\(\PageIndex{10}\). Si modelas las dos casas como el equivalente de una sola casa “efectiva” con una resistencia efectiva\(R\), ¿cuál es el valor de\(R\) en términos de\(R_{1}\) y\(R_{2}\)?
Solución:
El agua de la principal tendrá que fluir a través de la casa 1 o la casa 2. Si el caudal a través de la principal es\(Q\), requerimos que este sea igual a la suma de los caudales a través de cada casa:
\[\begin{aligned} Q=Q_{1}+Q_{2} \end{aligned}\]
El flujo a través de cada casa está relacionado con la diferencia de presión\(∆P\),, a través de cada casa (que es la misma), así como la resistencia de esa casa:
\[\begin{aligned} Q_{1}&=\frac{\Delta P}{R_{1}} \\ Q_{2}&=\frac{\Delta P}{R_{2}} \end{aligned}\]
El caudal total es así:
\[\begin{aligned} Q=Q_{1}+Q_{2}&=\frac{\Delta P}{R_{1}}+\frac{\Delta P}{R_{2}} \\ &=\Delta P \left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right) \end{aligned}\]
Podemos escribir esto como el flujo a través de una resistencia efectiva,\(R\), con una diferencia de presión\(∆P\):
\[\begin{aligned} Q&=\frac{\Delta P}{R} \\ \therefore R&=\frac{1}{\frac{1}{R_{1}}+\frac{1}{R_{2}}} \end{aligned}\]
Discusión:
Al exigir que la suma de los flujos de agua a través de las casas sea la misma que el caudal a través de la tubería principal, pudimos modelar las dos casas como una sola casa efectiva con resistencia\(R\). Podrán notar que esta es la misma relación que la resistencia equivalente para dos resistencias eléctricas combinadas en paralelo. Esto se debe a que el flujo de corriente eléctrica en una resistencia se puede modelar usando herramientas similares a las requeridas para modelar el flujo de un fluido viscoso en una tubería.
Notas al pie
1. Si la velocidad del fluido no es perpendicular a la superficie, entonces\(v\) es el componente de la velocidad perpendicular a la superficie.


