16.3: El Campo Eléctrico

Definimos el vector de campo eléctrico\(\vec E\), de manera análoga a como definimos el vector de campo gravitacional,\(\vec g\). Al definir el vector del campo gravitacional, digamos, en la superficie de la Tierra, podemos calcular fácilmente la fuerza gravitacional ejercida por la Tierra sobre cualquier masa,\(m\), sin tener que usar la Teoría Universal de la Gravedad de Newton. Como recordarán, podemos definir el campo gravitacional, en alguna posición\(\vec g(\vec r)\),\(\vec r\), a partir de una masa puntual,\(M\), como la fuerza gravitacional por unidad de masa:\[\begin{aligned} \vec g(\vec r) = -G \frac{M}{r^2}\hat r\end{aligned}\] donde\(\vec r\) es un vector de la posición de\(M\) a donde queremos conocer el campo gravitacional. En consecuencia, la fuerza ejercida sobre una “masa de prueba”\(m\), ubicada en la posición\(\vec r\) relativa a la masa\(M\) viene dada por:\[\begin{aligned} \vec F^g=m\vec g= -G\frac{Mm}{r^2}\hat r\end{aligned}\] que, por supuesto, es el resultado de la Teoría de la Gravedad de Newton. Como recordarán, podemos definir el campo gravitacional para cualquier objeto que no sea una masa puntual (por ejemplo, la Tierra), y usar ese campo para encontrar la fuerza ejercida por la Tierra sobre cualquier masa\(m\), sin tener que volver a calcular el campo gravitacional cada vez (lo que requiere una integral o Ley de Gauss ).

Se procede en un análogo fue definir el “Campo Eléctrico”,\(\vec E(\vec r)\), como la fuerza eléctrica por unidad de carga. Si tenemos una carga puntual,\(Q\), ubicada en el origen de un sistema de coordenadas, entonces el campo eléctrico desde ese punto carga\(\vec E(\vec r)\),, en alguna posición\(\vec r\),, relativa al origen viene dado por:

\[\vec E(\vec r)=k\frac{Q}{r^{2}}\hat r\]

Si colocamos una “carga de prueba”\(q\), en posición\(\vec r\) en el espacio, experimentará una fuerza dada por:\[\begin{aligned} \vec F^e=q\vec E=k\frac{Qq}{r^2}\hat r\end{aligned}\] tal como encontramos en la Ley de Coulomb.

Ejercicio\(\PageIndex{1}\)

Una carga negativa se coloca en el origen de un sistema de coordenadas. En algún momento del espacio, el campo eléctrico de esa carga

1. apunta hacia el origen.
2. señala lejos del origen.

Responder

En el Ejemplo 16.2.2, determinamos la fuerza eléctrica sobre carga\(q\), ejercida por otras dos cargas\(Q_1\) y\(Q_2\). Si ahora cambiamos el valor de\(q\) y quisiéramos determinar la fuerza, podemos utilizar el campo eléctrico para simplificar considerablemente el proceso. Es decir, podemos determinar el valor del campo eléctrico\(\vec E\), desde\(Q_1\) y\(Q_2\) en la posición de\(q\), y luego simplemente multiplicar ese vector de campo por una carga\(q\) para obtener la fuerza sobre esa carga, sin tener que añadir vectores de fuerza.

Ejemplo\(\PageIndex{1}\)

Dos cargas,\(Q_1=1\text{nC}\), y\(Q_2=-2\text{nC}\) se mantienen fijas en dos esquinas de un triángulo equilátero con lados de longitud\(a=1\text{cm}\), con un sistema de coordenadas como se muestra en la Figura\(\PageIndex{2}\). ¿Cuál es el vector de campo eléctrico en la tercera esquina del triángulo?

Figura\(\PageIndex{1}\): Dos cargas en las esquinas de un triángulo equilátero de lado\(a\).

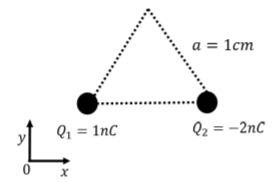
Solución:

El campo eléctrico neto en la tercera esquina del triángulo será la suma vectorial de los campos eléctricos a partir de cargas\(Q_1\) y\(Q_2\). Por lo tanto, necesitamos determinar los vectores de campo eléctrico de cada carga, y luego agregar esos dos vectores para obtener el campo eléctrico neto. Los vectores se ilustran en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Vectores de campo eléctrico de dos cargas en las esquinas de un triángulo equilátero de lado\(a\).

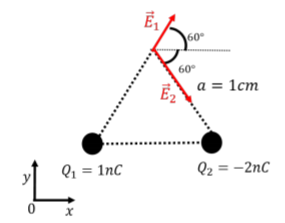
El campo eléctrico de carga\(Q_1\) tiene magnitud:\[\begin{aligned} E_1=\left |k\frac{Q_1}{a^2}\right |=(9\times 10^{9}\text{N}\cdot \text{m}^2\text{/C}^{2})\frac{(1\times 10^{-9}\text{C})}{(0.01\text{m})^2}=9\times 10^{4}\text{N/C}\end{aligned}\] y componentes:\[\begin{aligned} \vec E_1&=E_1\cos(60^{\circ})\hat x+E_1\sin(60^{\circ})\hat y\\ &=(4.5\times 10^{4}\text{N/C})\hat x+(7.8\times 10^{4}\text{N/C})\hat y\end{aligned}\] Del mismo modo, el campo eléctrico de\(Q_2\) tiene magnitud:\[\begin{aligned} E_2=\left |k\frac{Q_2}{a^2}\right |=(9\times 10^{9}\text{N}\cdot \text{m}^2\text{/C}^{2})\frac{(2\times 10^{-9}\text{C})}{(0.01\text{m})^2}=1.8\times 10^{5}\text{N/C}\end{aligned}\] y componentes:\[\begin{aligned} \vec E_2&=E_2\cos(60^{\circ})\hat x-E_2\sin(60^{\circ})\hat y\\ &=(9.0\times 10^{4}\text{N/C})\hat x-(1.6\times 10^{5}\text{N/C})\hat y\end{aligned}\] Finalmente, podemos sumar los dos vectores de fuerza juntos para obtener la fuerza neta en \(q\):\[\begin{aligned} \vec E^{net}&=\vec E_1+\vec E_2\\ &=(4.5\times 10^{4}\text{N/C})\hat x+(7.8\times 10^{4}\text{N/C})\hat y+(9.0\times 10^{4}\text{N/C})\hat x-(1.6\times 10^{5}\text{N/C})\hat y\\ &=(13.5\times 10^{4}\text{N/C})\hat x-(8.2\times 10^{4}\text{N/C})\hat y\end{aligned}\] que tiene una magnitud de\(15.8\times 10^{4}\text{N/C}\). Al conocer el campo eléctrico en la esquina vacía del triángulo, ahora podemos calcular la fuerza eléctrica neta que actuaría sobre cualquier carga colocada en esa ubicación. Por ejemplo, si colocamos una carga\(q=-1\text{nC}\) (como en el Ejemplo 16.2.2), podemos encontrar fácilmente la fuerza eléctrica correspondiente:\[\begin{aligned} \vec F_q &= q\vec E=(-1\text{nC})\left[ (13.5\times 10^{4}\text{N/C})\hat x-(8.2\times 10^{4}\text{N/C})\hat y \right]\\ &=-(13.5\times 10^{-5}\text{N})\hat x+(8.2\times 10^{-5}\text{N})\hat y\end{aligned}\] como encontramos anteriormente. Tenga en cuenta que la fuerza sobre\(q\) está en la dirección opuesta al vector de campo eléctrico. Esto se debe a que\(q\) es negativo. El campo eléctrico en algún punto del espacio apunta así en la misma dirección que la fuerza que experimentaría una carga de prueba positiva.

Discusión:

En este ejemplo, determinamos el campo eléctrico neto haciendo uso del principio de superposición; es decir, que podemos tratar los campos eléctricos desde\(Q_1\) e\(Q_2\) independientemente, sin necesidad de considerar el hecho de que\(Q_1\) y\(Q_2\) ejercer fuerzas unos sobre otros. Al conocer el campo eléctrico en alguna posición en el espacio, podemos calcular fácilmente el vector de fuerza en cualquier carga de prueba,\(q\), colocada en esa posición. Además, el signo de la carga\(q\) determinará en qué dirección apuntará la fuerza (paralela a\(\vec E\) para una carga positiva y antiparalela a\(\vec E\) para una carga negativa).

Ejercicio\(\PageIndex{2}\)

El campo eléctrico dentro de un conductor debe ser cero porque...

1. Si hay un campo eléctrico, los electrones se moverán (ya que es un conductor) y se organizarán para crear un campo adicional que cancele el campo original
2. Si hay un campo eléctrico, los protones se moverán (ya que es un conductor) y se organizarán para crear un campo adicional que cancele el campo original
3. Dado que los electrones pueden moverse libremente, se mueven tan rápido que el campo eléctrico es insignificante.
4. Los campos eléctricos no pueden penetrar los materiales conductores.

Responder

Visualización del campo eléctrico

Generalmente, un “campo” es algo que tiene un valor diferente en diferentes posiciones en el espacio. La presión en un fluido bajo la presencia de gravedad es un campo: la presión es diferente a diferentes alturas en el fluido. Dado que la presión es una cantidad escalar (un número), la llamamos “campo escalar”. Al campo eléctrico se le llama “campo vectorial”, porque es un vector que es diferente en cada posición en el espacio. Una forma de visualizar el campo eléctrico es dibujar flechas en diferentes posiciones en el espacio; la longitud de la flecha es entonces proporcional a la intensidad del campo eléctrico en esa posición, y la dirección de la flecha representa entonces la dirección del campo eléctrico. El campo eléctrico para una carga puntual se muestra usando este método en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Vectores de campo eléctrico cerca de una carga puntual.

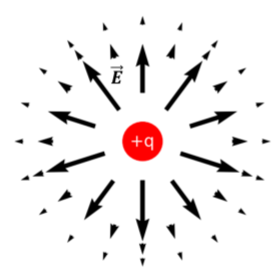
Una desventaja de visualizar un campo vectorial con flechas es que las flechas ocupan espacio, y puede ser un desafío visualizar cómo el campo cambia de magnitud y dirección continuamente a través del espacio. Por esta razón, se suele utilizar “líneas de campo” para visualizar un campo vectorial. Las líneas de campo son líneas continuas con las siguientes propiedades:

• La dirección del campo vectorial en algún punto del espacio es tangente a la línea de campo en ese punto.
• Las líneas de campo tienen una dirección para indicar la dirección del vector de campo a lo largo de la tangente (ya que hay dos posibilidades, paralela y antiparalela).
• La magnitud del campo es proporcional a la densidad de las líneas de campo en ese punto. Cuantas más líneas de campo estén cerca de una ubicación en el espacio, mayor será la magnitud del vector de campo en ese punto.

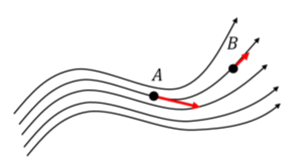
Un ejemplo del uso de líneas de campo para representar un campo vectorial en el espacio se muestra en la Figura\(\PageIndex{4}\). El vector de campo correspondiente se muestra en dos posiciones diferentes en el espacio (\(A\)y\(B\)). En ambas posiciones, el vector es tangente a la línea de campo en esa posición en el espacio y apunta en la dirección de la pequeña flecha dibujada al final de las líneas de campo. El vector de campo en el punto\(A\) tiene una magnitud mayor que el del punto\(B\), ya que las líneas de campo están más concentradas en el punto\(A\) que en el punto\(B\) (hay más líneas de campo por unidad de área en esa posición en el espacio, la las líneas de campo están más juntas).

Figura\(\PageIndex{4}\): Un ejemplo de determinación de un vector de campo a partir de las líneas de campo continuas.

Ejercicio\(\PageIndex{3}\)

¿Es posible que las líneas de campo se crucen?

1. Sí.
2. No.

Responder

Debido a que el vector de campo eléctrico siempre apunta en la dirección de la fuerza que se ejercería sobre una carga positiva, las líneas de campo eléctrico señalarán desde una carga positiva y hacia una carga negativa. Las líneas de campo eléctrico para una combinación de cargas positivas y negativas se ilustran en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Líneas de campo de dos\(+2q\) cargas y una\(-3q\) carga.

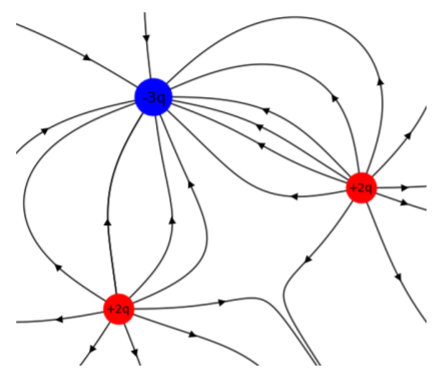
Campo eléctrico de una distribución de carga

Hasta el momento, solo hemos considerado la Ley de Coulomb para las cargas puntuales (cargas que son infinitamente pequeñas y pueden considerarse que existen en un solo punto en el espacio). Podemos usar el principio de superposición para determinar el campo eléctrico de un objeto cargado extendido/continuo modelando ese objeto como hecho de muchas cargas puntuales. El campo eléctrico de ese objeto es entonces la suma del campo eléctrico de las cargas puntuales que componen ese objeto.

Considere un cable cargado que se dobla en un semicírculo de radio\(R\), como en la Figura\(\PageIndex{6}\). El cable lleva una carga eléctrica positiva neta,\(+Q\), que se distribuye uniformemente a lo largo de la longitud del cable. Deseamos determinar el vector de campo eléctrico en el centro del círculo.

Figura\(\PageIndex{6}\): Un alambre cargado doblado en un semicírculo de radio\(R\).

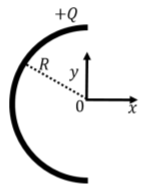
Comenzamos por elegir una sección muy pequeña de alambre y modelar esa sección de alambre como una carga puntual con carga infinitesimal\(dq\) (como en la Figura\(\PageIndex{7}\)). A distancia\(R\) de ese punto de carga, el campo eléctrico desde ese punto de carga tendrá magnitud,\(dE\), dada por:\[\begin{aligned} dE=k\frac{dq}{R^2}\end{aligned}\] El vector de campo eléctrico,\(d\vec E\), desde la carga puntual\(dq\) se ilustra en la Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\): Campos eléctricos infinitesimales a partir de cargas puntuales a lo largo del cable doblado.

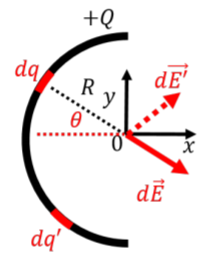
Utilizando el sistema de coordenadas que se muestra, definimos\(\theta\) como el ángulo realizado por el vector desde el origen hasta la carga puntual\(dq\) y el\(x\) eje -eje. El vector de campo eléctrico de\(dq\) viene dado entonces por:\[\begin{aligned} d\vec E = dE\cos\theta \hat x - dE\sin\theta \hat y\end{aligned}\] El campo eléctrico total en el origen se obtendrá sumando los campos eléctricos de los diferentes a lo\(dq\) largo de todo el semicírculo:\[\begin{aligned} \vec E &= \int d\vec E = \int \left(dE\cos\theta \hat x - dE\sin\theta \hat y\right)\\ &=\left( \int dE\cos\theta \right)\hat x -\left( \int dE\sin\theta \right)\hat y\\ \therefore E_x &= \int dE\cos\theta\\ \therefore E_y &= -\int dE\sin\theta\\\end{aligned}\] Nos quedan así con dos integrales para resolver para el \(x\)y\(y\) componentes del campo eléctrico, respectivamente. Antes de saltar a resolver las integrales, es útil pensar en la simetría del problema. Específicamente, considere una segunda carga puntual,\(dq'\), ubicada simétricamente alrededor del\(x\) eje -desde la carga\(dq\), como se ilustra en la Figura\(\PageIndex{7}\). La carga\(dq'\) creará un pequeño campo eléctrico\(d\vec E'\) como se ilustra. Cuando sumamos\(d\vec E\) y\(d\vec E'\), los dos\(y\) componentes se cancelarán, y solo los\(x\) componentes sumarán juntos. De igual manera, para cualquiera\(dq\) que escojamos, siempre habrá otro\(dq'\) tal que cuando sumemos juntos sus respectivos campos eléctricos, los\(y\) componentes cancelarán. Así, por simetría, podemos argumentar que el\(y\) componente neto del campo eléctrico,\(E_y\), debe ser idénticamente cero. Por lo tanto, solo necesitamos evaluar el\(x\) componente\[\begin{aligned} E_x = \int dE\cos\theta = \int k\frac{dq}{R^2} \cos\theta\end{aligned}\] de\(\vec E\): Para resolver esta integral, necesitamos considerar qué variables cambian para diferentes elecciones de la carga puntual\(dq\). En este caso, la distancia\(R\) es la misma en cualquier lugar a lo largo del semicírculo, por lo que sólo\(\theta\) cambia con diferentes opciones de\(dq\), como\(k\) es una constante. Podemos expresar\(dq\) en términos de\(d\theta\) y luego usar\(\theta\) como la variable de integración (la variable que etiqueta lo diferente\(dq\)). \(d\theta\)corresponde a un pequeño cambio en el ángulo\(\theta\), y es el ángulo que es subtendido por la carga\(dq\). Es decir, la carga\(dq\) cubre una pequeña longitud de arco,\(ds\), del semicírculo, que se relaciona\(d\theta\) con:\[\begin{aligned} ds = Rd\theta\end{aligned}\] La carga total en el cable viene dada por\(Q\), y el alambre tiene una longitud\(\pi R\) (la mitad del circunferencia de un círculo). Dado que la carga se distribuye uniformemente sobre el cable, la carga por unidad de longitud de cualquier pieza de alambre debe ser constante. En particular,\(dq\) dividido por\(ds\) debe ser igual a\(Q\) dividido por\(\pi R\):\[\begin{aligned} \frac{dq}{ds}&=\frac{Q}{\pi R}\\ \therefore dq &=\frac{Q}{\pi R}ds=\frac{Q}{\pi}d\theta\end{aligned}\] donde en la última igualdad usamos la relación\(ds=Rd\theta\). Ahora tenemos todos los ingredientes para resolver la integral:\[\begin{aligned} E_x &= \int k\frac{dq}{R^2} \cos\theta = \int_{-\pi/2}^{+\pi/2} k\frac{Q}{\pi R^2}\cos\theta d\theta\\ &= k\frac{Q}{\pi R^2}\int_{-\pi/2}^{+\pi/2}\cos\theta d\theta=k\frac{Q}{\pi R^2}\left[ \sin\theta \right]_{-\pi/2}^{+\pi/2}\\ &= k\frac{2Q}{\pi R^2}\end{aligned}\] El vector de campo eléctrico total en el centro del círculo viene así dado por:\[\begin{aligned} \vec E = k\frac{2Q}{\pi R^2} \hat x\end{aligned}\] Tenga en cuenta que si no nos hubiéramos dado cuenta de que no necesitábamos resolver la integral para el\(y\) componente, aún encontraríamos que es cero:\[\begin{aligned} E_y= -k\frac{Q}{\pi R^2}\int_{-\pi/2}^{+\pi/2}\cos\theta d\theta=-k\frac{Q}{\pi R^2}\left[ -\cos\theta \right]_{-\pi/2}^{+\pi/2}=0\end{aligned}\] Para determinar el campo eléctrico en algún momento a partir de cualquier distribución de carga continua, el procedimiento es generalmente el mismo:

1. Hacer un buen diagrama.
2. Elija un elemento de carga\(dq\).
3. Dibujar el elemento campo eléctrico,\(d\vec E\), en el punto de interés.
4. Escriba el vector de elemento de campo eléctrico,\(d\vec E\), en términos de\(dq\) y cualquier otra variable relevante.
5. Piense en la simetría: ¿alguno de los componentes de\(d\vec E\) suma a cero sobre todos los\(dq\)?
6. Escriba el campo eléctrico total como la suma (integral) de los elementos del campo eléctrico.
7. Identificar qué variables cambian a medida que una varía\(dq\) y elige una variable de integración para expresar\(dq\) y todo lo demás en términos de esa variable y otras constantes.
8. Hacer la suma (integral).

Ejemplo\(\PageIndex{2}\)

Un anillo de radio\(R\) carries a total charge \(+Q\). Determine the electric field a distance \(a\) from the center of the ring, along the axis of symmetry of the ring.

Solución:

Para determinar el campo eléctrico, realizamos el procedimiento descrito anteriormente, y comenzamos dibujando un buen diagrama, como en la Figura\(\PageIndex{8}\), mostrando: nuestro sistema de coordenadas, nuestra elección de\(dq\), el vector de elemento de campo eléctrico\(d\vec E\) que corresponde a \(dq\), y variables (\(r\),\(\theta\)) para especificar la posición de\(dq\).

Figura\(\PageIndex{8}\): Determinar el campo eléctrico en el eje de un anillo de radio\(R\) portando carga\(Q\).

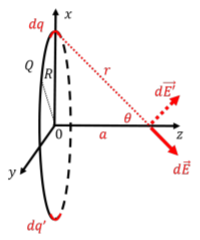
En este caso, la figura es un reto para dibujar y visualizar debido a la naturaleza tridimensional del problema. Con lo específico\(dq\) que elegimos, el vector de elemento de campo eléctrico viene dado por:\[\begin{aligned} d\vec E = -dE\sin\theta \hat x + 0\hat y + dE\cos\theta \hat z \end{aligned}\] donde\(d\vec E\) tiene magnitud:\[\begin{aligned} dE = k\frac{dq}{r^2}\end{aligned}\] Los\(x\) y\(z\) componentes del campo eléctrico total serán dados entonces por:\[\begin{aligned} E_x &= -\int dE\sin\theta=-\int k\frac{dq}{r^2}\sin\theta\\ E_z &= \int dE\cos\theta=\int k\frac{dq}{r^2}\cos\theta \\\end{aligned}\] En general, si hubiéramos elegido un\(dq\) que no esté a lo largo de uno de los ejes del sistema de coordenadas, el vector del elemento de campo eléctrico tendría componentes en las tres direcciones. Sin embargo, si consideramos la simetría del anillo, podemos notar que una vez que sumamos todos los elementos del campo eléctrico, solo sobrevivirán los\(z\) componentes. En efecto, hemos mostrado en la Figura\(\PageIndex{8}\) que para cada uno\(dq\), habrá un\(dq'\) ubicado en el lado opuesto del anillo que creará un elemento de campo eléctrico que cancelará todos menos el\(z\) componente del elemento de campo de \(dq\). Por lo tanto, solo necesitamos considerar los\(z\) componentes de los elementos del campo eléctrico al determinar el campo eléctrico total: Ahora\[\begin{aligned} \vec E = E_z\hat z\end{aligned}\] tenemos que evaluar la integral para el\(z\) componente del campo eléctrico:\[\begin{aligned} E_z &= \int k\frac{dq}{r^2}\cos\theta \\\end{aligned}\] y determinar qué cantidades cambian a medida que nos movemos\(dq\) alrededor del anillo. En este caso, ambos\(r^2\) y\(\cos\theta\) son iguales para todos los elementos del anillo, y la integral es trivial:\[\begin{aligned} E_z &= k\frac{1}{r^2}\cos\theta\int dq=k\frac{Q}{r^2}\cos\theta=kQ\frac{a}{(R^2+a^2)^\frac{3}{2}} \\\end{aligned}\] donde la integral\(\int dq\) simplemente significa “sumar todos los cargos\(dq\) juntos”, que es igual a \(Q\), la carga total en el anillo. En la última igualdad, sustituimos por\(\cos\theta\) las variables\(a\) y\(R\) que se proporcionan en la pregunta.

Ejemplo\(\PageIndex{3}\)

Se ha frotado una varilla de vidrio con un paño de seda de tal manera que la varilla de vidrio ha adquirido una carga positiva. La varilla tiene una longitud,\(L\), a negligible cross-section, and has acquired a total positive charge, \(+Q\), that is uniformly distributed along the length of the rod. What is the electric field a distance \(R\) from the center of the rod?

Solución:

Para determinar el campo eléctrico, realizamos el procedimiento descrito anteriormente, y comenzamos dibujando un buen diagrama, como en la Figura\(\PageIndex{9}\), mostrando: nuestro sistema de coordenadas, nuestra elección de\(dq\) a una distancia\(y\) por encima del centro de la varilla, el elemento de campo eléctrico vector\(d\vec E\) que corresponde a\(dq\), y variables (\(y\),\(r\),\(\theta\)) para especificar la posición de\(dq\).

Figura\(\PageIndex{9}\): Determinar el campo eléctrico a una distancia\(R\) desde el centro de una varilla de longitud\(L\) transportando carga\(Q\).

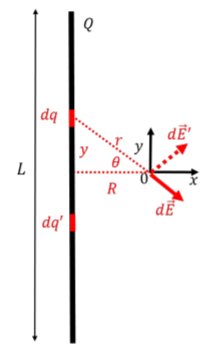
Definimos el origen que se ubicará en el punto donde queremos determinar el campo eléctrico, y el ángulo\(\theta\) para que sea el ángulo entre el vector horizontal y el vector de posición de\(dq\). Podemos escribir el vector de elemento de campo eléctrico como:\[\begin{aligned} d\vec E = dE\cos\theta \hat x - dE\sin\theta \hat y\end{aligned}\] donde\(d\vec E\) tiene magnitud:\[\begin{aligned} dE = k\frac{dq}{r^2}\end{aligned}\] Los\(x\) y\(y\) componentes del campo eléctrico total serán dados por:\[\begin{aligned} E_x &= \int dE\cos\theta=\int k\frac{dq}{r^2}\cos\theta \\ E_y &= -\int dE\sin\theta=-\int k\frac{dq}{r^2}\sin\theta\\\end{aligned}\] Nuevamente, antes de proceder con las integrales, consideramos simetría. Específicamente, si consideramos una carga\(dq'\) ubicada simétricamente alrededor del\(x\) eje desde\(dq\) (como se ilustra en la Figura\(\PageIndex{9}\)), vemos que el\(y\) componente del elemento de campo eléctrico\(d\vec E'\) que crea cancelará el\(y\) componente de\(d\vec E\). Para cada elección de\(dq\), existirá una elección correspondiente\(dq'\) que dará como resultado que el\(y\) componente del campo eléctrico neto sea cero. Por lo tanto, solo necesitamos evaluar el\(x\) componente del campo eléctrico total:\[\begin{aligned} \vec E = E_x \hat x = \left(\int k\frac{dq}{r^2}\cos\theta\right) \hat x\end{aligned}\] Dentro del integrando, ambos\(r\) y\(\theta\) cambiarán a medida que sumemos sobre las diferentes cargas\(dq\) a lo largo de la varilla. Una opción sencilla para escribir la integral es usarla\(y\) como constante de integración, y escribir\(dq\),\(r\), y\(\cos\theta\) en términos de\(y\). La carga\(dq\) cubre una longitud infinitesimal de la varilla,\(dy\). Dado que la varilla está cargada uniformemente, la carga por unidad de longitud debe ser la misma en una longitud\(dy\) pequeña que en toda la longitud de la varilla: A menudo\[\begin{aligned} \frac{dq}{dy}&=\frac{Q}{L}\\ \therefore dq &= \frac{Q}{L} dy\end{aligned}\] es útil introducir una carga constante por unidad de longitud\(\lambda=\frac{Q}{L}\),, para que podamos escribir la carga \(dq\)as: También\[\begin{aligned} dq = \lambda dy\end{aligned}\] podemos expresar\(r^2\) y\(\cos\theta\) en términos de\(y\) (y\(R\), que es constante):\[\begin{aligned} r^2 &= y^2+R^2\\ \cos\theta&=\frac{R}{r}=\frac{R}{\sqrt{y^2+R^2}}\end{aligned}\] Finalmente, podemos combinar todo esto en una integral que podamos evaluar:\[\begin{aligned} E_x &=\int k\frac{dq}{r^2}\cos\theta\\ &=k\int_{-L/2}^{L/2} \lambda \frac{1}{y^2+R^2}\frac{R}{\sqrt{y^2+R^2}} dy\\ &=kR\lambda\int_{-L/2}^{L/2} \frac{1}{(y^2+R^2)^{\frac{3}{2}}} dy\\ &=kR\lambda \left[ \frac{y}{R^2\sqrt{y^2+R^2}}\right]_{-L/2}^{L/2}\\ \therefore E_x &= \frac{k\lambda}{R}\frac{L}{\sqrt{\left(\frac{L}{2}\right)^2+R^2}} \end{aligned}\] Si el varilla eran infinitamente largas (o muy largas en comparación con la distancia\(R\)), el campo eléctrico se convierte en:\[\begin{aligned} \lim_{L\to\infty}E_x=\frac{2k\lambda}{R}\end{aligned}\] Al usar la carga por unidad de longitud\(\lambda\),, pudimos generalizar fácilmente nuestro resultado al esperado para una varilla infinitamente larga con densidad de carga uniforme.

Resolver la integral anterior en términos de la variable de integración\(y\) es difícil sin algún conocimiento de integrales. Para esta integral específica, el método más fácil de usar a partir del cálculo es la “sustitución trigonométrica”. A continuación mostramos cómo podemos llegar a una integral mucho más fácil si en cambio hubiéramos elegido el ángulo\(\theta\) como la variable de integración en lugar de\(y\), ¡y veremos que esta es una ilustración física del “método de sustitución trigonométrica” del cálculo!

Volvemos al paso 7 en nuestro procedimiento y elegimos\(\theta\) (en lugar de\(y\)) como la variable de integración para la integral: Es\[\begin{aligned} E_x &=\int k\frac{dq}{r^2}\cos\theta\\\end{aligned}\] decir, necesitamos expresarnos\(1/r^2\) y\(dq\) en términos de\(\theta\). Refiriéndose a la Figura\(\PageIndex{9}\), tenemos:\[\begin{aligned} r &= \frac{R}{\cos\theta}\\ \therefore \frac{1}{r^2}&=\frac{\cos^2\theta}{R^2}\\ y &= R\tan\theta\\ \therefore dy &= \frac{dy}{d\theta}d\theta=\frac{R}{\cos^2\theta}d\theta\\ \therefore dq &= \lambda dy =\lambda\frac{R}{\cos^2\theta}d\theta\end{aligned}\] La única dificultad está en determinar el ángulo\(d\theta\) subtendido por\(dq\), que se determinó anteriormente relacionando primero\(dy\) y\(d\theta\). Con estas sustituciones, la integral se vuelve trivial:\[\begin{aligned} E_x &=\int k\frac{dq}{r^2}\cos\theta\\ &=k\int_{-\theta_0}^{\theta_0} \lambda\frac{R}{\cos^2\theta} \frac{\cos^2\theta}{R^2} \cos\theta d\theta=\frac{k\lambda}{R}\int_{-\theta_0}^{\theta_0}\cos\theta d\theta=\frac{k\lambda}{R}\left[\sin\theta \right]_{-\theta_0}^{\theta_0}\\ &=\frac{2k\lambda}{R}\sin\theta_0\end{aligned}\] dónde\(\theta_0\) está el ángulo subtendido por la mitad de la varilla. Haciendo referencia a la Figura\(\PageIndex{9}\), podemos ver fácilmente que:\[\begin{aligned} \sin\theta_0=\frac{L/2}{\sqrt{\left(\frac{L}{2}\right)^2+R^2}}\end{aligned}\] Así que el campo eléctrico total viene dado por:\[\begin{aligned} E_x &=\frac{2k\lambda}{R}\sin\theta_0=\frac{k\lambda}{R}\frac{L}{\sqrt{\left(\frac{L}{2}\right)^2+R^2}}\end{aligned}\] como se encontró antes. Además, en el límite de una varilla infinitamente larga, el ángulo\(\theta_0\) tiende a\(\frac{\pi}{2}\), de manera que el campo eléctrico se convierte en:\[\begin{aligned} E_x=\lim_{\theta_0\to\frac{\pi}{2}}\frac{2k\lambda}{R}\sin\theta_0=\frac{2k\lambda}{R}\end{aligned}\] Discusión:

En este ejemplo, vimos cómo aplicar el principio de superposición para determinar el campo eléctrico cerca de una línea de carga finita y una infinita con carga constante por unidad de longitud. Demostramos que era relativamente sencillo establecer la integral en términos de\(dy\), pero no tan fácil de resolver la integral. Luego demostramos que al usar\(\theta\) como variable de integración, podríamos llegar a una integral mucho más fácil. Este cambio de variable corresponde a una variable física en nuestro problema, pero también es la base del método más abstracto de “sustitución trigonométrica” utilizado para resolver integrales en cálculo.

Ejemplo\(\PageIndex{4}\)

Calcular el campo eléctrico a distancia,\(a\), above a infinite plane that carries uniform charge per unit area, \(\sigma\).

Solución:

En este caso, necesitamos determinar el campo por encima de un objeto que es bidimensional (un plano). En los ejemplos anteriores (un anillo, una línea de carga), modelamos un objeto unidimensional (por ejemplo, la línea), como hecho de muchas cargas puntuales (objetos 0-dimensionales). Tratamos esas cargas puntuales que tiene una longitud infinitesimal a lo largo del objeto para que pudiéramos sumarlas juntas para obtener el objeto (por ejemplo,\(dy\) era la longitud de la carga para la varilla/línea de carga).

Para modelar el objeto bidimensional (el plano), lo modelizamos ha sido la suma de muchos objetos unidimensionales. Podemos modelar un plano ya sea como un rectángulo de ancho,\(W\), y largo\(L\), como se muestra en el panel izquierdo de la Figura\(\PageIndex{10}\) o como un disco de radio,\(R\), como se muestra en el panel derecho. Para modelar un plano infinito, entonces podemos tomar el límite de cualquiera\(L\) e\(W\) ir al infinito (rectángulo), o de\(R\) ir al infinito (disco). Podemos modelar el rectángulo como la suma de muchas líneas de longitud finita,\(L\), y ancho infinitesimal,\(dx\). Del mismo modo, podemos modelar el disco como la suma de anillos infinitesimalmente delgados de radio finito,\(r\), y grosor,\(dr\). En ambos casos, sabemos modelar el campo a partir de una línea de carga (Ejemplo 16.3.3) o desde un anillo (Ejemplo 16.3.2).

Figura\(\PageIndex{10}\): Un objeto bidimensional como un plano modelado como una suma de líneas infinitamente delgadas (panel izquierdo) o como la suma de anillos infinitamente delgados (panel derecho).

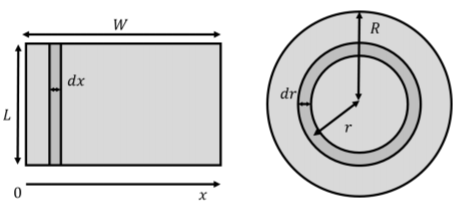
Se procede modelando el plano como un disco compuesto por anillos infinitesimales. Nuestra carga infinitesimal,\(dq\), es así la carga sobre un anillo de radio\(r\) y grosor\(dr\), como se ilustra en la Figura\(\PageIndex{11}\).

Figura\(\PageIndex{11}\): Modelado del campo a partir de un disco como la suma de campos de anillos delgados concéntricos.

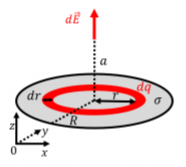
Sabemos por el Ejemplo 16.3.2 que la magnitud del campo eléctrico a una\(a\) distancia del centro del anillo, a lo largo de su eje de simetría (el\(z\) eje en la Figura\(\PageIndex{11}\)), viene dada\[\begin{aligned} dE = kdq\frac{a}{(r^2+a^2)^\frac{3}{2}} \end{aligned}\] por: Por simetría, para todos los diferentes anillos infinitesimales que conforman el disco, el campo siempre apuntará a lo largo del\(z\) eje. Para determinar el campo total, sumamos (integramos) los valores de\(dE\), sobre todos los anillos, de un radio de\(r=0\) a un radio\(r=R\). Para cada anillo, el valor de\(r\) será diferente, por lo que necesitamos expresarnos\(dq\) en términos de\(dr\) para poder realizar la integral. Sabemos que el avión tiene una carga uniforme por unidad de área dada por\(\sigma\). La carga\(dq\) de un anillo infinitesimal viene dada por:\[\begin{aligned} dq = \sigma dA=\sigma 2\pi r dr\end{aligned}\] dónde\(dA=2\pi r dr\) está el área del anillo infinitesimal de radio\(r\) y grosor\(dr\) (piense en desplegar el anillo en un rectángulo de altura \(dr\)y longitud\(2\pi r\), la circunferencia del círculo, para determinar el área). Ahora tenemos todos los ingredientes para determinar el campo eléctrico total:\[\begin{aligned} E &= \int dE = \int_0^R kdq\frac{a}{(r^2+a^2)^\frac{3}{2}} = 2\pi k a \sigma \int_0^R \frac{r}{(r^2+a^2)^\frac{3}{2}}dr\\ &=2\pi k a \sigma \left[ \frac{-1}{\sqrt{r^2+a^2}}\right]_0^R=2\pi k \sigma\left(1-\frac{a}{R^2+a^2} \right)\end{aligned}\] Finalmente, podemos tomar el límite de\(R\to\infty\) para conseguir el campo eléctrico por encima de un plano infinito:\[\begin{aligned} E=\lim_{R\to\infty}2\pi k \sigma\left(1-\frac{a}{R^2+a^2} \right)=2\pi k\sigma=\frac{\sigma}{2\epsilon_0}\end{aligned}\] donde usamos\(\epsilon_0\) en la última igualdad como resultado es un poco más limpio sin los factores de\(\pi\). Tenga en cuenta que para un plano de carga infinito, ¡el campo eléctrico no depende de la distancia (nuestra variable\(a\)) desde el plano!

Discusión:

En este ejemplo, mostramos cómo podemos modelar una distribución de carga bidimensional como la suma de distribuciones de carga unidimensionales. En particular, demostramos que un plano infinito de carga puede modelarse como la suma de muchas líneas de carga o de muchos anillos de carga (elegimos este último en lo anterior). También encontramos que el campo eléctrico por encima de un plano infinito de carga no depende de la distancia del plano; es decir, el campo eléctrico es constante por encima de un plano infinito de carga.

Pensamientos de josh

Una fuente común de confusión es el proceso de solución para el campo eléctrico producido por cargas continuas. Las cargas puntuales están bien definidas en el espacio como que están completamente contenidas dentro de un solo punto, mientras que las cargas continuas son objetos que ocupan 1, 2 o 3 dimensiones. El campo eléctrico producido por las cargas puntuales se modela fácilmente\(\vec E = \frac{kQ}{r^2}\hat r\), pero los campos eléctricos producidos por cargas continuas generalmente deben obtenerse de una integral.

Cuando se distribuye una carga, la carga sobre el objeto debe desglosarse en muchos cargos pequeños que se escriben como\(dq\). A partir de ahí,\(dq\) se reescribe en términos de una variable de posición sobre la cual es conveniente integrar. Piense en la variable de posición como una variable que puede utilizar para distinguir cargas,\(dq\), ubicadas en diferentes posiciones a lo largo del objeto.

Por ejemplo, refiriéndose a la Figura\(\PageIndex{12}\), si quisiera determinar\(E\) en la parte superior de una varilla (panel izquierdo), sería lo más conveniente para mí integrarlo sobre\(x\), pero si quisiera determinar\(E\) en el lado de una varilla, sería lo más conveniente para integrar sobre\(\theta\).

Figura\(\PageIndex{12}\): Cálculo del campo eléctrico producido por una varilla en diferentes posiciones.

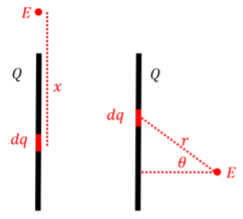
Para determinar los límites de la integral, piense en la variable de rango en posición que se requiere para cubrir todo el objeto. Recomiendo prestar mucha atención a los Ejemplos 16.3.2, 16.3.3 y 16.3.4, e intentar preguntas que requieran integración en la Biblioteca de Preguntas.