22.3: Ley de Ampere

La Ley de Ampere es similar a la Ley de Gauss, ya que nos permite determinar (analíticamente) el campo magnético que produce una corriente eléctrica en configuraciones que tienen un alto grado de simetría. La Ley de Ampere establece:

\[\oint\vec B\cdot d\vec l=\mu_{0}I^{enc}\]

donde la integral de la izquierda es una “integral de camino”, similar a como calculamos el trabajo realizado por una fuerza sobre un camino particular. El signo de círculo en la integral significa que esta es una integral sobre un camino “cerrado”; un camino donde los puntos de inicio y final son los mismos. \(I^{enc}\)es la corriente neta que cruza la superficie que está definida por el camino cerrado, a menudo llamado la “corriente encerrada” por el camino. Esto es diferente de la Ley de Gauss, donde la integral está sobre una superficie cerrada (no un camino cerrado, como es aquí). En el contexto de la Ley de Gauss, nos referimos a “calcular el flujo del campo eléctrico a través de una superficie cerrada”; en el contexto de la Ley de Ampere, nos referimos a “calcular la circulación del campo magnético a lo largo de un camino cerrado”.

Aplicamos la Ley de Ampere de la misma manera que aplicamos la Ley de Gauss.

Aplicación de la Ley de Ampere

1. Hacer un buen diagrama, identificar simetrías.
2. Elija una ruta cerrada sobre la que calcular la circulación del campo magnético (vea a continuación cómo elegir la ruta). El camino a menudo se llama un “bucle Amperiano” (piense en “superficie gaussiana”).
3. Evaluar la integral de circulación.
4. Determinar cuánta corriente está “encerrada” por el bucle Amperiano.
5. Aplicar Ley de Ampere.

De manera similar a la Ley de Gauss, necesitamos elegir el camino (en lugar de la superficie) sobre el que evaluaremos la integral. La integral será fácil de evaluar si:

1. El ángulo entre\(\vec B\) y\(d\vec l\) es constante a lo largo de la trayectoria, de modo que:

\[\begin{aligned} \oint\vec B\cdot d\vec l=\oint Bdl\cos\theta=\cos\theta\oint Bdl \end{aligned}\]

donde\(\theta\) esta el angulo entre\(\vec B\) y\(d\vec l\).

2. La magnitud de\(\vec B\) es constante a lo largo del camino, de manera que:

\[\begin{aligned} \cos\theta\oint Bdl=B\cos\theta\oint dl \end{aligned}\]

Elegir un camino que cumpla con estas dos condiciones sólo es posible si existe un alto grado de simetría.

Considera un cable recto infinitamente largo, llevando corriente,\(I\), fuera de la página, como se ilustra en la Figura\(\PageIndex{1}\). El campo magnético del cable debe tener el mismo aspecto independientemente del ángulo desde el que veamos el cable (“simetría acimutal”). Así, el campo magnético debe formar círculos concéntricos alrededor del alambre (que sabemos es el caso de la Ley Biot-Savart) o bien debe estar en la dirección radial (apuntando hacia o lejos del alambre). Estas dos posibilidades se ilustran en Figura\(\PageIndex{1}\), y vamos a pretender, por ahora, que no sabemos cuál es la correcta.

Figura\(\PageIndex{1}\): Por simetría, el campo magnético de un cable infinito portador de corriente (ilustrado con la corriente que sale de la página), debe formar círculos concéntricos (panel izquierdo), o estar en la dirección radial (panel derecho). Sabemos que el primero (círculos, panel izquierdo) es la elección correcta. Las líneas punteadas muestran “bucles Amperianos” que se pueden utilizar para calcular la integral en la Ley de Ampere.

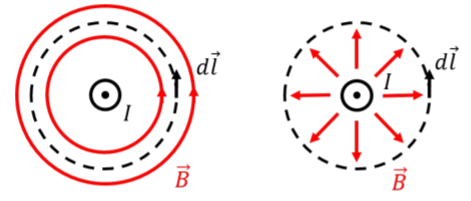
Para aplicar la Ley de Amp`ere, elegimos un bucle Amperiano (en lugar de una “superficie gaussiana”). En el caso de un cable portador de corriente infinito, un círculo que es concéntrico con el alambre cumplirá con las propiedades anteriores, independientemente de las dos configuraciones posibles del campo magnético: con un bucle circular Amperiano, el ángulo entre el campo magnético y el elemento\(d\vec l\) es constante a lo largo del bucle entero, y la magnitud del campo magnético es constante a lo largo del bucle. Nuestra elección de bucle se ilustra en la Figura\(\PageIndex{2}\), donde hemos ilustrado el campo magnético para el caso en el que forma círculos concéntricos.

Figura\(\PageIndex{2}\): Un bucle Amperiano que es un círculo de radio\(h\),, nos permitirá determinar el campo magnético a una distancia,\(h\), a partir de un cable portador de corriente infinitamente largo.

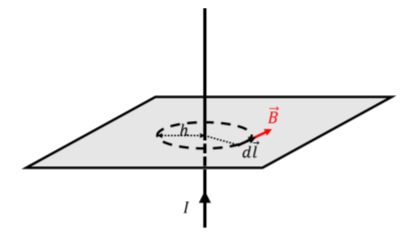
La circulación del campo magnético a lo largo de una trayectoria circular de radio,\(h\), viene dada por:

\[\begin{aligned} \oint\vec B\cdot d\vec l=\oint Bdl\cos\theta =\cos\theta\oint Bdl=B\cos\theta\oint dl=B\cos\theta (2\pi h) \end{aligned}\]

donde\(\cos θ\) es\(1\) si el campo forma círculos (correcto) o\(0\) si el campo es radial (incorrecto). Ahora podemos evaluar la corriente que está encerrada por el bucle Amperiano. La corriente que se encierra viene dada por la corriente neta que atraviesa la superficie definida por el bucle Amperiano (en este caso, un círculo de radio\(h\)). Dado que el bucle encierra todo el cable, la corriente encerrada es simplemente,\(I\). Aplicando la Ley de Ampere:

\[\begin{aligned} \oint\vec B\cdot d\vec l&=\mu_{0}I^{enc} \\ B\cos\theta (2\pi h)&=\mu_{0}I \end{aligned}\]

En este punto, es claro que cos θ no puede ser cero, ya que el lado derecho de la ecuación no es cero. Podemos concluir así que el campo magnético debe efectivamente hacer círculos concéntricos, como habíamos determinado previamente. La magnitud del campo magnético viene dada por:

\[\begin{aligned} B=\frac{\mu_{0}I}{2\pi h} \end{aligned}\]

como encontramos anteriormente con la Ley Biot-Savart. Nuevamente, en analogía con la Ley de Gauss, es necesario aplicar algunos conocimientos de simetría y argumentar en qué dirección debería apuntar el campo magnético, para poder utilizar la Ley de Ampere de manera efectiva.

Ejercicio\(\PageIndex{1}\)

La ley de Ampere demuestra que el campo magnético en el centro de un bucle portador de corriente es cero porque no hay corriente cerrada:

1. Cierto.
2. Falso

Responder

Ejemplo\(\PageIndex{1}\)

Un cable uniforme sólido largo de radio,\(R\), transporta corriente,\(I\), con una densidad de corriente que es uniforme a través de la sección transversal del cable. Determinar la intensidad del campo magnético en función de,\(r\), la distancia desde el centro del cable, dentro y fuera del cable.

Solución:

En este caso, necesitamos determinar el campo magnético tanto dentro como fuera del cable. La figura\(\PageIndex{3}\) muestra dos bucles circulares de Amperiano que podemos usar para aplicar la Ley de Amperios para determinar el campo magnético dentro y fuera del cable.

Figura\(\PageIndex{3}\): Dos bucles circulares Amperianos para determinar la magnitud del campo magnético dentro y fuera de un cable de radio portador de corriente,\(R\) (con corriente uniforme que sale de la página).

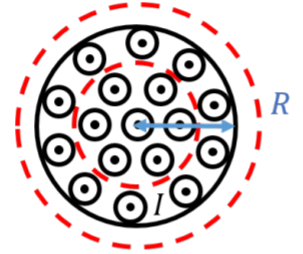
Por simetría, y siguiendo la discusión en este capítulo, sabemos que el campo magnético debe formar círculos concéntricos, tanto dentro como fuera del cable. Fuera del cable, procedemos de la misma manera que anteriormente, eligiendo un bucle Amperiano de radio,\(r > R\), de tal manera que la circulación viene dada por:

\[\begin{aligned} \oint\vec B\cdot d\vec l=B2\pi r \end{aligned}\]

Todo el cable está encerrado por el bucle, de manera que la corriente encerrada es,\(I\). Así, la Ley de Ampere da:

\[\begin{aligned} \oint\vec B\cdot d\vec l&=\mu_{0}I^{enc} \\ B(2\pi r)&=\mu_{0}I \\ \therefore B&=\frac{\mu_{0}I}{2\pi r}\quad(r\geq R) \end{aligned}\]

Dentro del cable, la circulación integral alrededor de una trayectoria circular de radio,\(r < R\), es la misma:

\[\begin{aligned} \oint\vec B\cdot d\vec l=B2\pi r \end{aligned}\]

Sin embargo, en este caso, el bucle Amperiano más pequeño no encierra toda la corriente que fluye a través del cable. Nos dicen que la densidad de corriente,\(j\), es uniforme en el cable. Podemos así determinar la corriente por unidad de área (es decir, la densidad de corriente) que fluye a través de todo el cable, y usarla para determinar cuánta corriente fluye a través de la superficie con área\(πr^{2}\) que es definida por el bucle Amperiano:

\[\begin{aligned} j&=\frac{I}{A}=\frac{I}{\pi R^{2}} \\ \therefore I^{enc}&=j(\pi r^{2})=\frac{I}{\pi R^{2}}(\pi r^{2})=I\frac{r^{2}}{R^{2}} \end{aligned}\]

Finalmente, podemos aplicar la Ley de Amp`ere para determinar la magnitud del campo magnético dentro del cable:

\[\begin{aligned} \oint\vec B\cdot d\vec l&=\mu_{0}I^{enc} \\ B(2\pi r)&=\mu_{0}I\frac{r^{2}}{R^{2}} \\ \therefore B&=\frac{\mu_{0}I}{2\pi R^{2}}r \end{aligned}\]

y encontramos que el campo magnético es cero en el centro del cable (r = 0), y aumenta linealmente hasta el borde del cable\((r = R)\).

Discusión:

En este ejemplo, utilizamos la Ley de Ampere para modelar la fuerza del campo magnético dentro y fuera de un cable portador de corriente. Para aplicar la Ley de Ampere dentro del cable, tomamos en cuenta que sólo una fracción de la corriente está encerrada por el bucle Amperiano. Este problema es análogo a aplicar la Ley de Gauss para determinar el campo eléctrico dentro y fuera de una esfera con carga uniforme.

Interpretación de la Ley de Ampere y cálculo vectorial

En esta sección, discutimos la Ley de Amp`ere en el contexto del cálculo vectorial y brindamos una perspectiva diferente, principalmente con fines informativos. La integral que aparece en la Ley de Ampere se llama la “circulación” del campo vectorial,\(\vec B\):

\[\begin{aligned} \oint\vec B\cdot d\vec l \end{aligned}\]

La circulación, como su nombre lo indica, es una medida de “cuánta rotación hay en el campo”. Para visualizar esto, imagine que el campo vectorial es un campo de velocidad para puntos en un fluido. Las regiones del fluido donde hay pequeños remolinos (los llamados “remolinos”), corresponden a regiones del campo con circulación distinta de cero (el signo de la integral nos indica el sentido de rotación, usando la regla de la derecha para vectores axiales). En la Figura se muestran ejemplos de campo con y sin circulación\(\PageIndex{4}\). Reconocerá que las cargas eléctricas estáticas crean campos eléctricos sin circulación (panel derecho), mientras que las corrientes estáticas crean campos magnéticos con circulación.

Figura\(\PageIndex{4}\): Ejemplos de campo con circulación (panel izquierdo) y sin (panel derecho), evaluados a lo largo del bucle cerrado que se muestra con la línea discontinua.

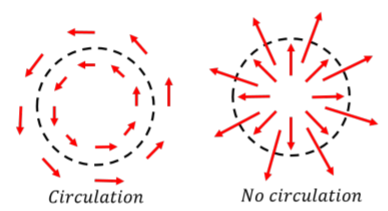
La Ley de Ampere es así una afirmación de que una corriente eléctrica dará como resultado un campo con una magnitud proporcional a la corriente, que tiene cierto grado de rotación a la misma. El sentido de rotación de ese campo corresponde a la regla de la derecha para vectores axiales tal como se aplica a la corriente (tu pulgar apunta en la dirección de la corriente para que tus dedos se doblen en la dirección de la rotación del campo asociado).

La circulación, como la define la integral sobre un bucle cerrado, no es una propiedad local del campo, ya que depende de lo que el campo esté haciendo en su conjunto sobre la trayectoria del bucle. Así como se puede obtener una versión “local” de la Ley de Gauss, también se puede obtener una versión local de la Ley de Amp`ere utilizando técnicas de cálculo vectorial avanzado (que están más allá del alcance de este libro de texto).

El teorema de Stokes permite convertir la integral de circulación (una integral de ruta en un bucle cerrado) en una integral sobre la superficie (abierta) que es definida por el bucle:

\[\begin{aligned} \oint_{C}\vec Bd\vec l=\int_{S}(\nabla\times\vec B)\cdot d\vec A \end{aligned}\]

donde el subíndice\(C\) indica que la integral está sobre una trayectoria unidimensional, mientras que el subíndice\(S\) indica que la integral está sobre una superficie bidimensional. El término,\(∇ × \vec B\), se llama el “rizo” del campo magnético y es una medida local de la cantidad de rotación en el campo. Aplicando el teorema de Stokes al rendimiento de la Ley de Ampere:

\[\begin{aligned} \oint\vec B\cdot d\vec l&=\mu_{0}I^{enc} \\ \int_{S}(\nabla\times\vec B)\cdot d\vec A=\mu_{0}I^{enc} \end{aligned}\]

Tenga en cuenta que también podemos escribir la corriente,\(I^{enc}\), que está encerrada por el bucle como la integral de la densidad de corriente\(\vec j\),, sobre la superficie definida por el bucle:

\[\begin{aligned} I^{enc}=\int_{S}\vec j\cdot d\vec A \end{aligned}\]

Así, podemos escribir la Ley de Ampere con integrales sobre la misma superficie a cada lado de la ecuación, implicando que los enteros deben ser los mismos:

\[\begin{aligned} \int_{S}(\nabla\times\vec B)\cdot d\vec A=\mu_{0}\int_{S}\vec j\cdot d\vec A \end{aligned}\]

\[\therefore\nabla\times\vec B=\mu_{0}\vec j\]

Esta última ecuación relaciona ahora una propiedad local (densidad de corriente) con el campo magnético en ese punto, y es la forma habitual en la que se presenta la Ley de Ampere (la llamada “forma diferencial”, más que la “forma integral”).

El rizo del campo magnético,\(∇ × \vec B\), es un vector que viene dado por lo siguiente:

\[\begin{aligned} \nabla\times\vec B=\left(\frac{\partial B_{z}}{\partial y}-\frac{\partial B_{y}}{\partial z} \right)\hat x+\left(\frac{\partial B_{x}}{\partial z}-\frac{\partial B_{z}}{\partial x} \right)\hat y +\left( \frac{\partial B_{y}}{\partial x}-\frac{\partial B_{x}}{\partial y} \right)\hat z \end{aligned}\]

y se elige el nombre “curl” porque esta es una medida de la cantidad de rotación (curl) en el campo. En forma diferencial, la Ley de Ampere puede leer como: “una densidad de corriente creará un campo (magnético) que tiene un rizo distinto de cero”.

Dado que la Ley de Ampere en forma diferencial es una ecuación vectorial (ambos lados son vectores), realmente corresponde a tres ecuaciones en coordenadas cartesianas, una por componente. Por ejemplo, el\(x\) componente de la ecuación es una “ecuación diferencial parcial” para los\(z\) componentes\(y\) y del campo magnético:

\[\begin{aligned} \left(\frac{\partial B_{z}}{\partial y}-\frac{\partial B_{y}}{\partial z} \right)=\mu_{0}j_{x} \end{aligned}\]

que en general es difícil de resolver sin una computadora (y se requieren las tres ecuaciones, ya que éstas están “acopladas”, ya que un componente dado del campo magnético aparece en dos de tres ecuaciones).