10.E: Postulados de Einstein (Ejercicios)

10.1

Supongamos que se despierta en Rotterdam (a 10 km de Delft) 1 minuto antes de que comience la clase en Delft (es decir, a las 8:44). Te vistes rápido, pero solo te quedan 10 segundos para llegar a Delft. Resulta que eres un motociclista muy rápido, lo que lo hace exactamente cuando tu reloj muestra las 8:45. ¿El resto de la clase estará de acuerdo en que llegaste justo a tiempo?

10.2

Una cita conocida (pero probablemente apócrifa) de Einstein es 'Siéntate en una estufa caliente durante cinco minutos, y se siente como una hora. Habla con una chica guapa durante una hora, y se siente como cinco minutos. Eso es la relatividad”.

(a) Einstein (en reposo, marco\(S\)) se sienta sobre alfileres y agujas durante cinco minutos. ¿Podría haber un marco móvil\(S_0\) en el que este mismo periodo dure una hora? Si es así, determinar la velocidad de ese cuadro con respecto a\(S\), si no, explicar por qué no.

b) Einstein conversa con Marilyn Monroe durante una hora. (Según otra anécdota conocida, durante esta conversación Marilyn Monroe le habría dicho a Einstein 'Si tuviéramos hijos, y ellos tendrían tu cerebro y mi apariencia, ¿no sería fantástico? ' , a lo que Einstein respondió 'Sí, pero ¿y si ellos tuvieran tu cerebro y mi apariencia? '). Tanto Einstein como Monroe están en reposo en marco\(S\). ¿Podría haber un marco móvil\(S_0\) en el que este mismo periodo dure cinco minutos? Si es así, determinar la velocidad de ese cuadro con respecto a S, si no, explique por qué no.

10.3

¿Qué tan rápido tendrías que volar de tal manera que cubras exactamente un año luz (medido por un observador estacionario) en un año (medido en tu reloj)?

10.4

Añadiendo velocidades Einstein postuló que la velocidad de la luz (en vacío, pero ignoraremos ese punto) es la misma en cualquier marco de referencia inercial. En consecuencia, para cualquier objeto con masa, la velocidad de la luz es también el límite absoluto: nunca se puede llegar a él, y mucho menos superarlo. Eso no encaja bien con la experiencia cotidiana: si estás en un tren que se mueve a velocidad\(u\) y lanzas una pelota a velocidad\(v\), un observador externo (estacionario) medirá la velocidad de la pelota para ser\(u + v\). Parece que no hay ninguna razón fundamental por la que no pudiéramos tomar, digamos,\(u=v=0.8c\), lo que implicaría que el observador externo mide el balón para ir a\(1.6c\). Lo extraño es que (es) no lo hace -el observador externo te dirá que midieron una velocidad de sólo\(0.976c\). El motivo es que aunque tanto tú como el observador externo consideran que la velocidad es la distancia recorrida dividida por el tiempo que tardó en recorrer esa distancia, ya no mides ni la misma distancia ni el mismo tiempo a velocidades tan altas. En este ejercicio, derivaremos una nueva ecuación para sumar velocidades, lo que demuestra que nunca se puede romper el límite de velocidad de la luz.

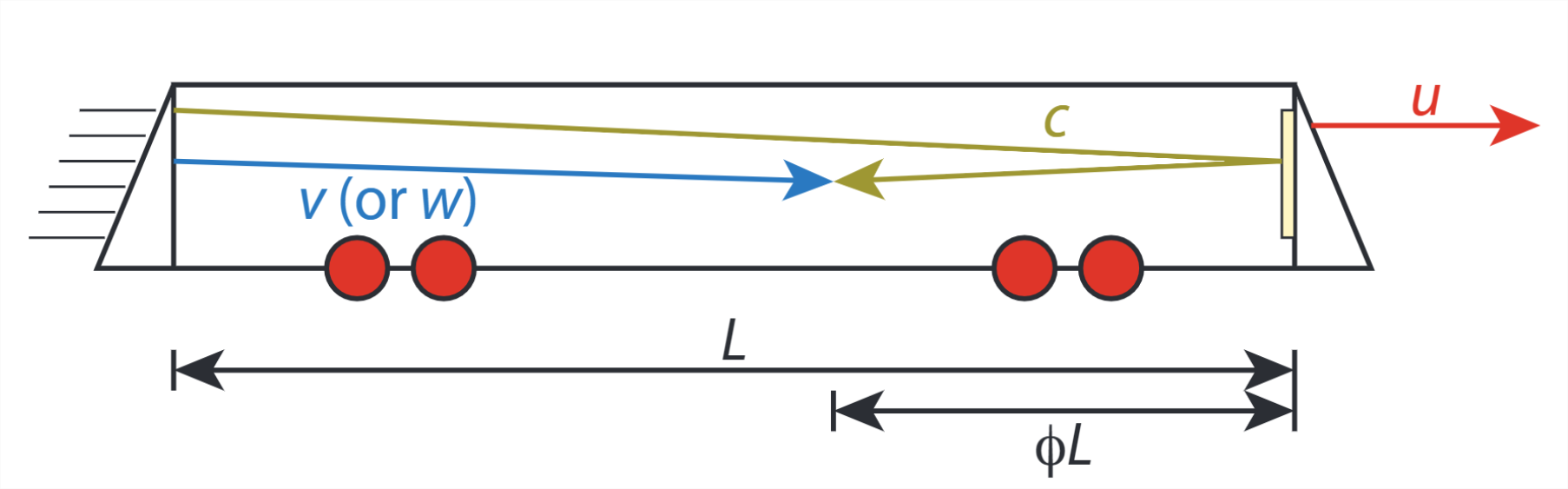
Consideramos la situación esbozada en figura\(\PageIndex{1}\). Un tren se mueve con velocidad\(u\). Alguien parado en la parte trasera del vagón del tren dispara un fotón (amarillo, velocidad\(c\)) y una bala (azul) al mismo tiempo. Según se mide en el tren, la bala tiene velocidad\(v\); para un observador externo, la bala tiene velocidad\(w\). El fotón es reflejado por un espejo en la parte delantera del automóvil, y se encuentra con la bala en un punto a una\(\phi L\) distancia del frente. Tenga en cuenta que\(L\), la longitud del automóvil, se mide de manera diferente por el observador comoving y estacionario (exterior), al igual que el intervalo de tiempo entre el disparo y la reunión del fotón y la bala. No obstante, ambos observadores coinciden en que ante los eventos de disparo y encuentro el fotón y la bala están en el mismo lugar en el espacio y en el tiempo. Usaremos estos dos puntos para encontrar una relación entre las velocidades de la bala observadas en el marco estacionario y comoving, y la velocidad del tren.

(a) Primero, tomarás el punto de vista (y las coordenadas espacio-tiempo) del observador externo. Denote la longitud del tren (según lo observado por ti) por\(L\), el tiempo que tarda el fotón en llegar al frente del tren\(t_1\), y el tiempo que tarda en regresar al punto de encuentro\(t_2\). El tren se mueve a velocidad\(u\), la velocidad observada de la bala es\(w\) y la del fotón es (obviamente)\(c\). Express\(ct_1\), la distancia recorrida por el fotón en\(t_1\), en términos de\(L\)\(u\), y\(t_1\).

(b) Ahora exprese\(ct_2\), la distancia recorrida por el fotón en\(t_2\), en términos de\(L\)\(u\),\(t_2\), y\(\phi\).

(c) A partir de las dos ecuaciones que tiene, elimine\(L\) y luego reescriba la ecuación resultante en una expresión para\(t_2/t_1\).

d) Argumentar que\(w\left(t_{1}+t_{2}\right)=c\left(t_{1}-t_{2}\right)\) al considerar dónde se encuentran la bala y el fotón.

(e) Reescribir la expresión en (4d) para dar también una expresión para\(t_2/t_1\).

(f) Equipar las expresiones que encontraste en (4c) y (4e), luego vuelve a escribirlas como una expresión para\(\phi\).

(g) Ahora tomaremos el punto de vista comoving. Encuentra otra expresión para\(\phi\). Sugerencia: puede repetir el procedimiento anterior para el observador comoving, o 'traducir' la expresión en (4f) directamente al marco comoving.

(h) Equiparar las dos expresiones\(\phi\) para obtener una expresión para\(w\) que sólo contenga\(u\),\(v\) y\(c\).

(i) El resto es álgebra: mostrar que la expresión que encontraste en (4h) se puede reescribir como:\[w=\frac{v+u}{1+u v / c^{2}}\].

Figura\(\PageIndex{1}\): Una persona parada en la parte trasera de un vagón de tren en movimiento dispara un fotón y una bala al mismo tiempo. El fotón se refleja en un espejo en la parte delantera del tren, y se encuentra con la bala algún tiempo después.

10.5

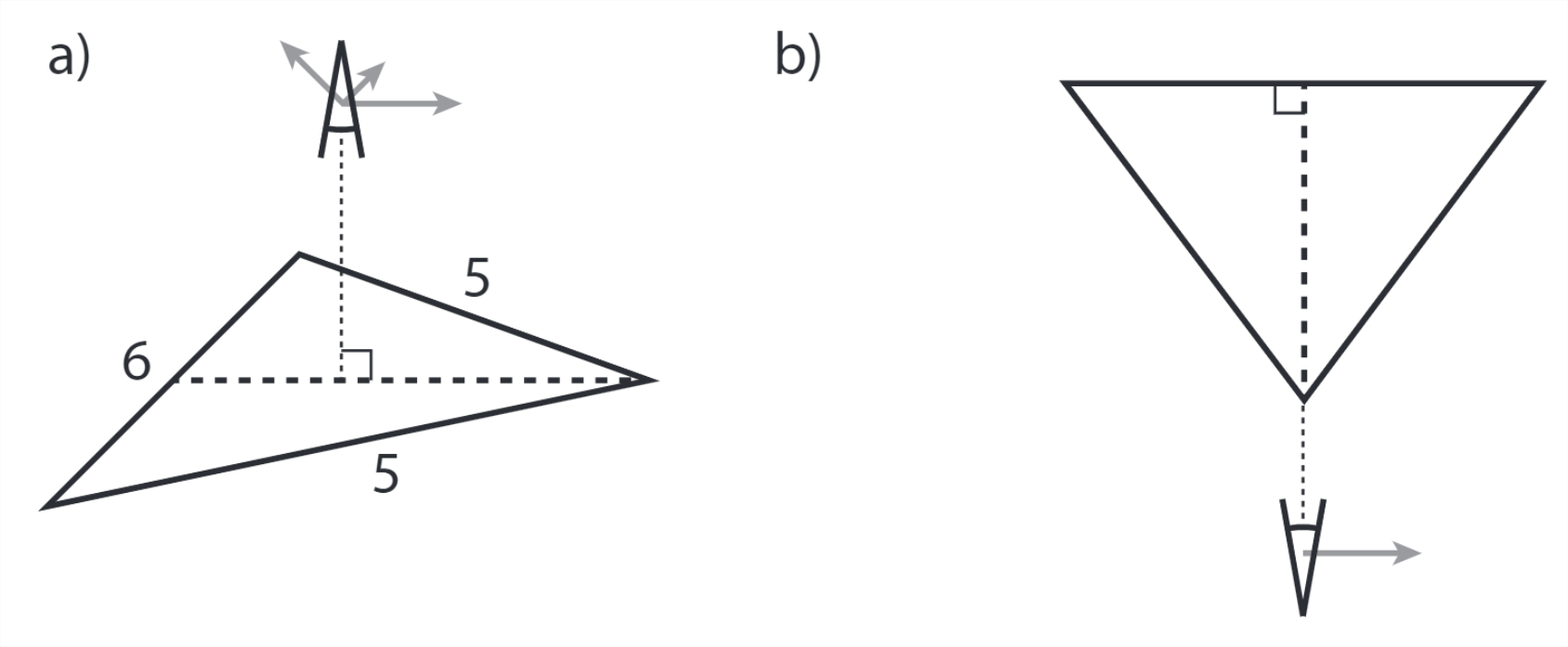
[Desafiante] Tres barras se sueldan juntas en forma de triángulo isósceles con relaciones laterales 5:5:6. Un observador mira nuestro triángulo desde una dirección perpendicular al plano que abarca, como en la figura A. El observador se mueve con velocidad relativista\(v\) en una dirección paralela al plano del triángulo.

a) ¿En qué dirección y a qué velocidad debería moverse el observador para que según él, el triángulo sea equilátero?

(b) Ahora giramos el triángulo de tal manera que todas sus esquinas y el observador estén en un plano. El lado más largo del triángulo está dispuesto perpendicular a la línea de visión del observador, y en el extremo más alejado, como en la figura b. El observador se mueve con velocidad\(v\) (no necesariamente la misma velocidad que en la parte (a) en la dirección paralela a este borde largo. Mostrar que el observador ve un triángulo distorsionado.

(c) A medida que el observador siga moviéndose por la misma línea que en (b), mostrar que le parece como si el triángulo estuviera girando, y determinar en qué dirección gira.