10.2: Consecuencias de los postulados de Einstein
- Page ID
- 129660
La combinación de los dos postulados en la sección 10.1 lleva a una serie de consecuencias que parecen estar en desacuerdo con la experiencia cotidiana. Implican que no existen cosas como medidas universales de tiempo y duración, ni siquiera un acuerdo sobre si los eventos son simultáneos o no. La razón por la que no observamos estas consecuencias todo el tiempo es que sus efectos son muy pequeños para objetos que se mueven lentamente (en comparación con la velocidad de la luz). Sin embargo, sí existen y se pueden medir -y importan mucho en situaciones donde las velocidades son altas, como en aceleradores de partículas y radiación cósmica.
PÉRDIDA DE SIMULTANEIDAD
Considera el siguiente experimento (pensamiento). Alguien se para en medio de un vagón de tren con espejos en cada extremo. El carro se mueve a velocidad constante\(v\) con respecto a la plataforma, en la que colocamos un segundo observador. La persona en el tren sostiene dos punteros láser, que presiona al mismo tiempo (o tal vez un dispositivo con un solo botón que envía dos haces, para evitar el sesgo del experimentador). Según la persona del tren, las vigas llegan a ambos espejos simultáneamente, ya que viajan a la misma velocidad, y cubren la misma distancia. Ahora según la persona en la plataforma, las vigas también viajan a la misma velocidad (!) - El postulado de luz de Einstein nos dice que todos los observadores miden la velocidad de la luz para ser iguales. No obstante, según este observador estacionario, el tren también se mueve, y así el haz de luz que viaja al frente del tren tiene que cubrir una distancia mayor que la que va a la parte trasera del tren. En consecuencia, la viga que viaja hacia atrás llega a su espejo antes que la que viaja hacia adelante. Nos vemos obligados a concluir que los eventos que son simultáneos en un marco de referencia inercial no son necesariamente simultáneos en otro.
Afortunadamente, hay un evento en el que ambos observadores coinciden: el hecho de que los dos haces de luz, una vez reflejados, regresen a la persona en medio del tren al mismo tiempo. Desde el punto de vista de la persona en el tren esto es obvio. Para la persona en la plataforma, un cálculo simple muestra que la distancia que gana el rayo hacia atrás en el viaje de ida es igual a la distancia que pierde en el viaje de regreso, y viceversa. Diferentes observadores no están de acuerdo en general en la simultaneidad (o incluso el orden) de los eventos que ocurren en diferentes puntos del espacio, pero sí coinciden en el orden de los eventos en un punto dado del espacio, lo que significa que la relatividad preserva la causalidad (el concepto que causa precede a los efectos).
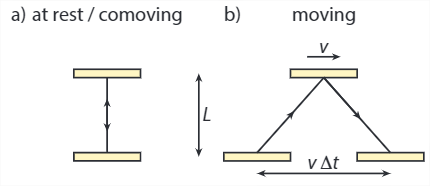
DILATACIÓN DEL TIEMPO
Dado que todos coinciden en la velocidad de la luz (y muy poco más), tiene sentido usar la velocidad de la luz para determinar otras cantidades físicas, como el intervalo de tiempo entre dos eventos. Para ello, podemos construir un reloj de luz: colocamos dos espejos en paralelo, y dejamos que un haz de luz rebote de un lado a otro entre ellos (Figura\(\PageIndex{1}\)). Ya que estamos de acuerdo en al menos el orden de los eventos en el mismo punto en el espacio, tomemos como nuestro intervalo de tiempo el tiempo que tarda la luz en viajar de un lado a otro entre los espejos una vez (es decir, un viaje de ida y vuelta). Según el observador comoving (cuyas coordenadas denotaremos con primos, y cuyo sistema de coordenadas llamaremos\(S'\)), este intervalo de tiempo viene dado por\(\Delta t' = 2L/c\), ya que la distancia recorrida por la luz es simplemente el doble de la distancia perpendicular entre los espejos. Sin embargo, para el observador estacionario parece que la luz también se ha movido en dirección paralela a los espejos (ver figura\(\PageIndex(1)\) b). Denotaremos su sistema de coordenadas como\(S\), con intervalo de tiempo\(\Delta\). La distancia total recorrida por la luz es (invocando el teorema de Pitágoras)\(\sqrt{(2L)^2 + (v\Delta t)^2)}\), que debe ser igual\(c\Delta t\). Resolviendo para\(\Delta t\), encontramos\( (\Delta t)^2 = (2L)^2/(c^2 -v^2) \), que es más largo que el intervalo de tiempo medido por el observador comoving (eso tiene sentido - si la luz viaja a la misma velocidad, una distancia mayor debería tomar más tiempo). Los dos intervalos de tiempo están relacionados por:
\[ \Delta t = \frac{1}{\sqrt{1-v^2/c^2}}\Delta t' = \gamma (v) \Delta t' \]
El factor\(\gamma (v)\) volverá frecuentemente en este capítulo. Su valor es uno si\(v = 0\), y se hace progresivamente más grande a medida que\(v\) aumenta, para explotar en\(v = c\). Para 'pequeño' (comparado con c) valores\(v\) del valor de\(\gamma (v)\) es muy cercano a uno, razón por la cual los efectos de la relatividad especial casi nunca aparecen en la vida cotidiana.
Hemos establecido que los intervalos de tiempo entre dos eventos son diferentes para dos observadores diferentes (comoving y estacionarios). Hay un punto sutil pero importante que hacer sobre cómo se percibe el tiempo para progresar según un solo observador. Empecemos con el observador estacionario. Supongamos que este observador mide el tiempo con un reloj de luz en su propio marco de referencia, y observa un reloj de luz idéntico en un tren en movimiento. Dado que el intervalo de tiempo para el viaje de ida y vuelta de la luz en el reloj de luz comoving (o en este caso, coestacionario) se mide para que sea menor que el del reloj en movimiento, el observador estacionario concluye que el reloj en movimiento está funcionando lento. Esta observación es universal, y se conoce como dilatación temporal. Para enfatizar lo universal que es la dilatación del tiempo, considera el punto de vista de la persona en el tren: según ella, su reloj está funcionando 'normal', mientras que el reloj en la plataforma corre lento -lo cual está en perfecta concordancia con la afirmación anterior, ya que desde el punto de vista del tren, es la plataforma la que es en movimiento.
Experimento Michelson-Morley
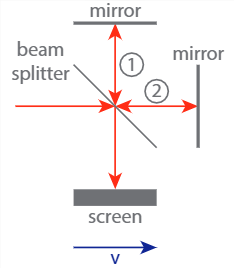
El experimento Michelson-Morley (1887) fue un intento de medir el movimiento relativo de la Tierra con respecto al éter, sustancia que se postuló para llenar todo el espacio. Era bien sabido en el siglo XIX que la atmósfera de la Tierra sólo se extiende a unos 100 km de altura, y dado que la luz solar puede llegar a la Tierra, se postuló que debe haber otra sustancia que actuara como medio para la propagación de la luz (al igual que el sonido se propaga a través del aire, el agua, o incluso los sólidos, pero no a través del vacío). Dado que la Tierra se mueve alrededor del sol, debe moverse relativamente al éter, o desde el punto de vista de un observador en la Tierra, el éter debe fluir a través del espacio ('viento etére'). En consecuencia, el éter debe afectar la velocidad de la luz para un haz que viaja en la misma dirección que el viento, pero no uno que viaje perpendicular a esta dirección. Michelson y Morley intentaron utilizar este principio para medir la velocidad del viento etéreo, con un dispositivo ahora conocido como interferómetro Michelson (en la foto). Sin embargo, no encontraron ninguna diferencia, para ningún ángulo de los brazos del interferómetro. Lorentz (ver cuadro siguiente) inicialmente intentó explicar este resultado introduciendo el concepto de 'tiempo local', lo que llevaría a una contracción Lorentz de uno de los brazos con respecto al otro, cancelando el efecto del viento etéreo. Einstein tomó un enfoque más radical, dejando caer por completo el concepto del éter, y reemplazándolo por sus dos postulados, que tienen la contracción de Lorentz como una de sus consecuencias. Recientemente se han utilizado tres interferómetros Michelson (muy sensibles) para detectar pequeñas vibraciones en el propio espacio-tiempo, las ondas gravitacionales predichas por la teoría general de la relatividad de Einstein.
Si el aparato se mueve hacia la derecha con velocidad\(v\), la velocidad de la luz en la trayectoria 1 (arriba-abajo) viene dada por\( u_1 = |\textbf{u}_1| = \sqrt{c^2 - v^2}\). Si la distancia entre el divisor de haz y el espejo es\(L\), el tiempo que tarda en atravesar la trayectoria 1 (ida y vuelta) viene dado por
\[ t_{1}=\frac{2 L}{u_{1}}=\frac{2 L}{\sqrt{c^{2}-v^{2}}}=\frac{2 L / c}{\sqrt{1-(v / c)^{2}}} .\]
Para la trayectoria 2, la velocidad de la luz al salir al espejo es igual\( u_{out} = c-v\), mientras que la velocidad en la trayectoria de retorno es igual\(u_{in} = c+v\). El tiempo total para la trayectoria (también de longitud\(L\)) por lo tanto es igual a
\[ t_{2}=\frac{L}{c-v}+\frac{L}{c+v}=\frac{2 L / c}{1-(v / c)^{2}}=\frac{1}{\sqrt{1-(v / c)^{2}}} t_{1},\]
así que el camino 2 siempre toma menos tiempo que el camino 1. (Tenga en cuenta que el factor de proporcionalidad es exactamente el mismo que el que encontraremos relacionando el tiempo observado por un observador comoving y un observador estacionario en la imagen relativista - ¡Lorentz no estaba tan lejos!). Sin embargo, si la velocidad de la luz es idéntica en las trayectorias 1 y 2, el tiempo que lleva atravesar cualquiera de ellas también es idéntico, y no esperamos ninguna interferencia.
Un ejemplo bastante famoso del efecto de la dilatación del tiempo es la observación del número de muones de alta velocidad (partículas similares a los electrones, pero mucho más pesadas e inestables) en la superficie de la tierra. Los muones se crean en la atmósfera superior (unos 20 km arriba), cuando los rayos cósmicos chocan con los átomos atmosféricos. Los muones tienen un medio tiempo de decaimiento de 2.2\(\mu\) s (lo que significa que después de este tiempo la mitad de los muones originales han decaído). Los muones se crean a muy alta velocidad, cerca de la de light (\(v = 0.999c\)). Aun así, clásicamente sólo pueden recorrer unos 650 m antes de que la mitad de ellos se hayan ido, y casi ninguno llegará a la superficie de la tierra. No obstante, dado que según nosotros los observadores estacionarios en la tierra los relojes de los muones corren lentos, esperamos que el medio tiempo se extienda efectivamente con un factor\(\gamma (0.999c)=22\), resultando en una distancia de unos 15 km antes de que la mitad de ellos hayan decaído, y que un número significativo llegue a la superficie, como se observa.
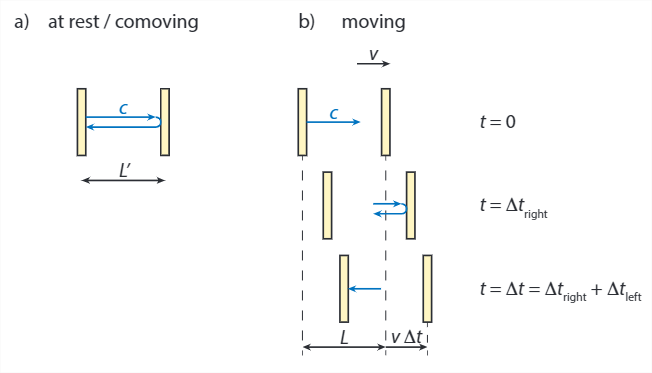
CONTRACCIÓN LORENTZ
No solo los observadores en diferentes marcos inerciales no están de acuerdo sobre la duración en intervalos de tiempo, tampoco coinciden en la longitud de los objetos (es decir, el tamaño de los intervalos espaciales). Para distancias perpendiculares a una dirección de movimiento no hay problema: para el reloj de luz en la figura\(\PageIndex{1}\), ambos observadores miden una distancia\(L\) entre los dos espejos. No obstante, si se les preguntara sobre, digamos, la longitud del vagón del tren en el que estamos imaginando estar el observador en movimiento, sus respuestas no estarían de acuerdo.
Para ver cómo se produce esta diferencia en la longitud medida y cómo se relacionan las longitudes, volvemos al reloj de luz, pero ahora lo giramos de lado (figura\(\PageIndex{3}\)) 1. Para ambos observadores, la medición de la distancia entre los espejos se puede hacer midiendo el tiempo que tarda un rayo de luz en hacer un viaje de ida y vuelta entre ellos. Para el observador comoving, lo encontramos\( L' = \frac{1}{2}c\Delta t' \). Para el observador estacionario, la imagen es más complicada, ya que los espejos se mueven mientras la luz viaja. Al salir, la distancia que tiene que recorrer la luz es la distancia\(L\) entre los espejos, más la distancia que se mueve\(v\Delta t_{right}\) el espejo lejano. Esta distancia total debe ser igual\( c\Delta t_{right}\), así que obtenemos\( \Delta t_{right} = L/(c-v) \). En el camino de regreso, obtenemos una distancia recorrida de\(L\) menos\( v\Delta t_{left} \), que debería ser igual\(c\Delta t_{left}\), así que obtenemos\( \Delta t_{left} = L/(c+v) \). El tiempo total recorrido es la suma de estos dos, que viene dada por:
\[\Delta t = \Delta t_{right} + \Delta t_{left} = \frac{L}{c-v} + \frac{L}{c+v} = \frac{2Lc}{c^2-v^2}\]
o
\[L=\frac{c^{2}-v^{2}}{2 c} \Delta t=\frac{c^{2}-v^{2}}{2 c} \gamma(v) \Delta t^{\prime}=\frac{c^{2}-v^{2}}{c^{2}} \gamma(v) L^{\prime}=\frac{1}{\gamma(v)} L^{\prime} \label{eq:1}\]
Las dos longitudes están así relacionadas por la inversa del\(\gamma\) factor que relaciona dos intervalos de tiempo. Usando un argumento similar al de los relojes (relacionando la longitud de dos palos idénticos, uno estacionario y otro móvil), podemos concluir que las longitudes móviles se contraen, un efecto conocido como contracción de Lorentz. Existe una interesante simetría entre la dilatación del tiempo y la contracción de Lorentz, lo que da una forma alternativa de obtener la ecuación (\(\ref{eq:1}\)) una vez que se conoce el efecto de la dilatación del tiempo. Consideremos de nuevo el ejemplo de los muones, pero ahora van al marco co-moviéndose con los muones. En este marco, el medio tiempo de decaimiento sigue siendo de 2.2\(\mu\) s, pero el mismo número de muones alcanzan la superficie de la tierra que en el marco estacionario. El motivo es que según los muones, la distancia desde la atmósfera superior a la superficie se contrae, exactamente por un factor 1/\(\gamma (v)\), lo que da la misma distancia de 15 km a la que la mitad de ellos han decaído.
1 Alternativamente, podemos decir que medimos la longitud del vagón del tren enviando un haz de luz de ida y vuelta en el vagón, rebotando en un espejo al final.

