11.E: Transformaciones de Lorentz (Ejercicios)
- Page ID
- 129698
11.1
Supongamos que el sistema\(S^\prime\) se mueve\(S\) con respecto a la velocidad\(u\), y\(S^{\prime\prime}\) se mueve con respecto a\(S^\prime\) con la velocidad\(v\). Mostrar ese sistema\(S^{\prime\prime}\) y\(S\) están relacionados a través de una transformación de Lorentz con la velocidad
\[w=\frac{u+v}{1+\frac{uv}{c^2}}.\]
11.2
La ecuación (11.13) da la transformación de Lorentz para un observador que se mueve en una dirección arbitraria\(\textbf{u}\).
(a) Demostrar que si se emite un rayo de luz en el marco de reposo\(S\) en una dirección arbitraria, de tal manera que su trayectoria se describe por\(\textbf{x}=\textbf{c}t\) (dónde\(\textbf{c}\cdot\textbf{c}=c^2\)), entonces en el marco móvil\(S^\prime\), la trayectoria del rayo de luz es también una línea recta, dada por\(\textbf{x}^\prime=\textbf{c}^\prime t^\prime\), con\(\textbf{c}^\prime\cdot\textbf{c}^\prime=c^2\).
b) ¿Cuál es la dirección del rayo de luz\(S^\prime\)?
11.3
a) Tanto un estudiante como una alumna asisten a conferencias sobre relatividad. Después, regresan a casa en tren, moviéndose en direcciones opuestas, cada una en\((4/5)c\). Antes de irse, prometieron enviarse mensajes entre ellos mientras estaban en el tren. Desafortunadamente hay interferencia en la red telefónica, por lo que no pueden usar sus teléfonos para hacerlo. Sin embargo, sí tienen pluma y papel, así podrían anotar su mensaje y tirarlo al otro tren. El chico, habiendo solo prestado atención durante la primera parte de la conferencia (siendo distraído por la niña después) recuerda que nada puede ir más rápido que la velocidad de la luz, y concluye que lanzar algo no tiene sentido, ya que la velocidad relativa (clásica) de los trenes supera a la velocidad de la luz. La niña, que prestó atención en todo momento, se da cuenta de que este no es el caso, y explica por qué en su nota al niño. ¿A qué velocidad mínima debería lanzar la nota para que pueda llegar al tren del chico?
(b) El niño, habiendo recibido el mensaje de la niña, se da cuenta de que tiene muchas más posibilidades de completar las tareas si puede hacerle algunas preguntas más. Por lo tanto, abandona su tren, y toma el siguiente de regreso (por lo que ahora viaja en la misma dirección que la niña). Desafortunadamente, este tren solo se mueve en\((3/5)c\), por lo que no alcanzará el tren de la niña. El chico se consuela con la idea de que respecto a él, la niña se mueve, por lo que su reloj va lento, y al menos no se habrá olvidado de él para cuando salga de su tren. Pasa una hora en el reloj del niño. ¿Cuánto tiempo (según él) ha avanzado el reloj de la niña en ese periodo (suponiendo que ambos permanezcan en sus trenes)?
11.4
Un observador en la Tierra ve dos naves espaciales (o trenes, lo que prefieras) acercándose desde direcciones opuestas. El observador mide sus velocidades en su propio marco de descanso, y al no conocer la relatividad, utiliza la adición de velocidad galilea para concluir que las dos naves espaciales tienen una velocidad relativa de\((7/5)v\). Sin embargo, un observador en una de las naves espaciales mide la velocidad relativa de la otra como\((35/37)c\). Encuentra las velocidades de las dos naves espaciales relativas a la Tierra.
11.5
Tanto un estudiante como una alumna asisten a conferencias de relatividad. El chico sin embargo está más interesado en la niña que en la conferencia. Frustrado, el maestro arroja una esponja mojada hacia él, a gran velocidad\(c/2\). La niña, con la esperanza de salvar al niño, intenta interceptar la esponja, arrojándole su marcador desde un lado (haciendo un ángulo recto, es decir, llegando a la esponja desde una dirección perpendicular a su dirección de movimiento, como se ve en el marco de referencia (estacionario) de la sala de conferencias) con velocidad\(c/3\). Para una araña que pasa a sentarse sobre la esponja, ¿cuál es la velocidad medida del marcador?
11.6
Una nave espacial vuela lejos de la Tierra con velocidad\(c/3\). Después de algún tiempo un pequeño transbordador parte de la nave espacial, en una dirección que hace un ángulo recto con el de la nave principal, y una velocidad de\(c/4\), medida en el resto del marco de la nave principal. ¿Cuál es la magnitud y dirección de la velocidad de la lanzadera medida desde la Tierra?
Ángulos en transformaciones de Lorentz
(a) Una varilla se mueve con velocidad\(v\) en línea recta con relación a un marco inercial\(S\). En su marco de reposo la varilla hace un ángulo de\(\theta^\prime\) con la dirección hacia delante de su movimiento. Encuentra el ángulo que\(\theta\) la varilla parece hacer con la dirección del movimiento medida en el marco\(S\). Determinar el valor numérico de este ángulo para\(\theta^\prime=60^\circ\) y\(v=3c/5\).
(b) Como se observa desde un marco inercial\(S\), un espejo se mueve con velocidad\(v\) en la\(x\) dirección con su superficie plana perpendicular a\(x\). También como se observa en el marco\(S\), un fotón que viaja en el\(xy\) plano incide sobre la superficie del espejo con un ángulo con respecto\(theta\) a la normal del espejo. Demostrar que, como se ve desde\(S\), el fotón reflejado tiene un ángulo\(\bar{\theta}\) con el espejo normal, donde
\[\cos \bar{\theta}=\frac{\cos \theta+\cos \alpha}{1+\cos \theta \cos \alpha},\]
y\(\cos\alpha=2(v/c)/(1+(v/c)^2)\).
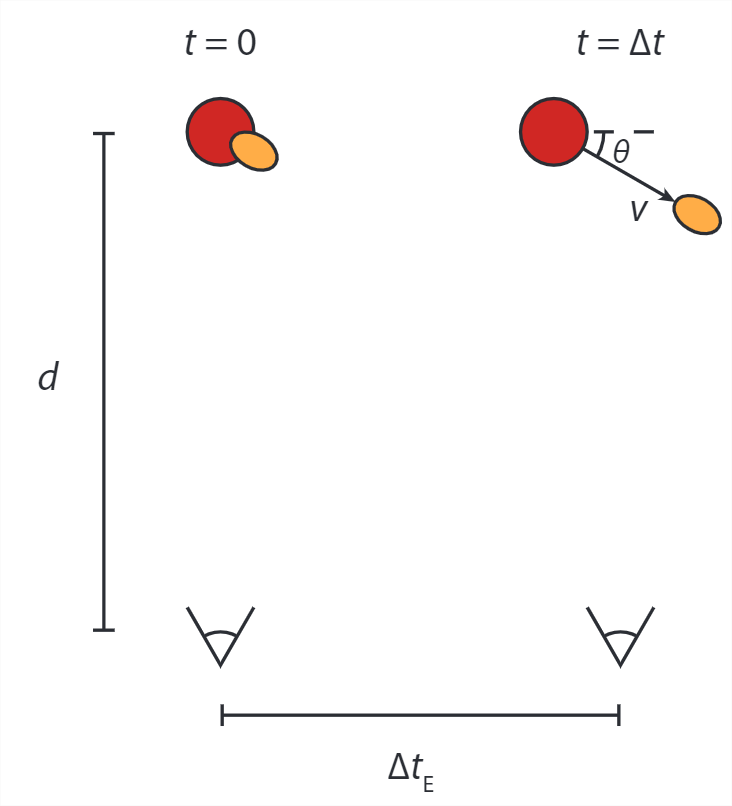
Figura\(\PageIndex{1}\): Observando la explosión de un cuásar a gran distancia.
11.8
Los cuásares son núcleos galácticos activos que pueden emitir grandes cantidades de materia, generalmente gas. Afortunadamente están lo suficientemente lejos como para no afectarnos nunca, pero lo suficientemente cerca como para que podamos medir por ejemplo la velocidad del gas emitido. Estas velocidades ocasionalmente parecen superar la velocidad de la luz. Para ver cómo puede suceder esto, considere un cuásar a una\(d\) distancia de la Tierra (medido en el marco de descanso colectivo de la Tierra y el cuásar), y una explosión en el cuásar que resulte en tal emisión en\(t=0\), ver figura\(\PageIndex{1}\). La luz emitida en el momento de la explosión llega a la Tierra en\(t=d/c\). Si el gas emitido se mueve en una trayectoria como la que se muestra en la figura de abajo, la luz emitida por el gas tiene que viajar una distancia más corta a la Tierra que la luz emitida en el momento de la explosión. La luz emitida por una explosión en un cuásar distante llega a la Tierra después de un intervalo de tiempo\(d/c\). La luz emitida por el gas expulsado tiene que recorrer una distancia más corta. Obsérvese que la distancia recorrida por el gas es mucho menor que la distancia entre la Tierra y el cuásar, por lo que la luz que llega de ambos puede tomarse como proveniente de la misma dirección. Supongamos que el gas viaja a velocidad\(v\).
(a) Determinar el intervalo\(\Delta t_E\) entre los eventos 'El observador de la Tierra ve la explosión inicial' (que ocurre en el cuásar en\(t=0\), pero se observa más tarde) y 'El observador de la Tierra ve la luz emitida por el gas en el\(t\) momento'.
(b) Determinar la velocidad del gas que mediría un astrónomo de la Tierra si no toma\(theta\) en cuenta el ángulo (a esta velocidad la llamamos\(v_{obs}\)).
(c) Demostrar que la velocidad observada puede superar la velocidad de la luz.
(d) Demostrar que para dada la velocidad real\(v\) del gas, la velocidad observada se maximiza si\(\sin\theta = v/c\), y que en ese caso obtenemos\(v_{obs}=\gamma(v)v\).
e) ¿Cuál es la velocidad mínima\(v\) para el gas a la que puede parecer tener una velocidad igual a la de la luz?
11.9
[Para la sección 11.4] Demostrar la última igualdad en la ecuación (11.4.6) expandiendo las tangentes hiperbólicas en la fracción en funciones exponenciales.
11.10
[Para la sección 11.4] Probar la ecuación (11.4.9) por inducción. Si esta es la primera vez que demuestras algo por inducción: el paso 1 es demostrar que la ecuación se mantiene para\(n=1\) (completamente trivial en la mayoría de los casos); el paso 2 es demostrar que si la ecuación se mantiene para todos los valores hasta\(n\), también se mantiene para\(n+1\). En este caso, así hay que calcular\(u_{n+1}\) (relativisticamente) sumando\(u\) y\(u_n\).

