13.7: Poder Aplicado por una Fuerza Constante

Supongamos que una fuerza aplicada\(\overrightarrow{\mathbf{F}}^{a}\) actúa sobre un cuerpo durante un intervalo de tiempo\(\Delta t\) y el desplazamiento del punto de aplicación de la fuerza es en la dirección x en una cantidad\(\Delta x\). El trabajo realizado,\(\Delta W^{a}\), durante este intervalo es

\[\Delta W^{a}=F_{x}^{a} \Delta x \nonumber \]

donde\(F_{x}^{a}\) es el componente x de la fuerza aplicada. (La Ecuación (13.7.1) es lo mismo que la Ecuación (13.4.2).)

La potencia media de una fuerza aplicada se define como la velocidad a la que se realiza el trabajo,

\[P_{a v e}^{a}=\frac{\Delta W^{a}}{\Delta t}=\frac{F_{x}^{a} \Delta x}{\Delta t}=F_{x}^{a} v_{\text {ave }, x} \nonumber \]

La potencia promedio entregada al cuerpo es igual al componente de la fuerza en la dirección del movimiento multiplicado por el componente de la velocidad promedio del cuerpo. La potencia es una cantidad escalar y puede ser positiva, cero o negativa dependiendo del signo de trabajo. Las unidades SI de potencia se denominan vatios [W] y\([1 \mathrm{W}]=\left[1 \mathrm{J} \cdot \mathrm{s}^{-1}\right]\).

La potencia instantánea en el tiempo t se define como el límite de la potencia promedio a medida que el intervalo de tiempo\([t, t+\Delta t]\) se acerca a cero,

\[P^{a}=\lim _{\Delta t \rightarrow 0} \frac{\Delta W^{a}}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{F_{x}^{a} \Delta x}{\Delta t}=F_{x}^{a}\left(\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}\right)=F_{x}^{a} v_{x} \nonumber \]

La potencia instantánea de una fuerza aplicada constante es el producto de la componente de la fuerza en la dirección del movimiento y la velocidad instantánea del objeto en movimiento.

Ejemplo\(\PageIndex{1}\): Gravitational Power for a Falling Object

Supongamos que una bola\(m=0.2 \mathrm{kg}\) de masa parte del reposo a una altura\(y_{0}=15 \mathrm{m}\) por encima de la superficie de la tierra y cae a una altura\(y_{f}=5.0 \mathrm{m}\) por encima de la superficie de la tierra. ¿Cuál es el poder promedio que ejerce la fuerza de gravitación? ¿Cuál es el poder instantáneo cuando la pelota está a una altura\(y_{f}=5.0 \mathrm{m}\) por encima de la superficie de la Tierra? Haz una gráfica de potencia vs. tiempo. Puede ignorar los efectos de la resistencia al aire.

Solución

Hay dos formas de resolver este problema. Ambos enfoques requieren calcular el intervalo de tiempo\(\Delta t\) para que la pelota caiga. Establecido\(t_{0}=0\) para el momento en que se soltó la pelota. Podemos resolver para el intervalo de tiempo\(\Delta t=t_{f}\) que tarda la pelota en caer usando la ecuación para un objeto que cae libremente que parte del descanso,

\[y_{f}=y_{0}-\frac{1}{2} g t_{f}^{2} \nonumber \]

Así, el intervalo de tiempo para la caída es

\[t_{f}=\sqrt{\frac{2}{g}\left(y_{0}-y_{f}\right)}=\sqrt{\frac{2}{9.8 \mathrm{m} \cdot \mathrm{s}^{-2}}(15 \mathrm{m}-5 \mathrm{m})}=1.4 \mathrm{s} \nonumber \]

Primer acercamiento: podemos calcular el trabajo realizado por gravedad,

\ [\ begin {alineado}
W^ {g} &=-m g\ izquierda (y_ {f} -y_ {0}\ derecha)\\
&=\ izquierda (-2.0\ veces 10^ {-1}\ mathrm {kg}\ derecha)\ izquierda (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ derecha) (5\ mathrm {m} -15\ mathrm {m}) =2.0\ veces 10^ {1}\ mathrm {J}
\ final {alineado}\ nonumber\]

Entonces la potencia promedio es

\[P_{\text {ave }}^{g}=\frac{\Delta W}{\Delta t}=\frac{2.0 \times 10^{1} \mathrm{J}}{1.4 \mathrm{s}}=1.4 \times 10^{1} \mathrm{W} \nonumber \]

Segundo Enfoque. Calculamos la fuerza de gravitación y la velocidad promedio. La fuerza de gravitación es

\[F_{y}^{g}=-m g=-\left(2.0 \times 10^{-1} \mathrm{kg}\right)\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)=-2.0 \mathrm{N} \nonumber \]

La velocidad promedio es

\[v_{\text {ave } y}=\frac{\Delta y}{\Delta t}=\frac{5 \mathrm{m}-15 \mathrm{m}}{1.4 \mathrm{s}}=-7.0 \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

Por lo tanto, la potencia promedio es

\ [\ begin {alineado}
P_ {\ text {ave}} ^ {g} &=F_ {y} ^ {g} v_ {\ text {ave} y} =( -m g) v_ {\ texto {ave}, y}\\
& =( -2.0\ mathrm {N})\ left (-7.0\ mathrm {m}\ cdot\ mathrm {s} ^ ^ -1}\ derecha) =1.4\ veces 10^ {1}\ mathrm {W}
\ final {alineado}\ nonumber\]

Para encontrar la potencia instantánea en cualquier momento, necesitamos encontrar la velocidad instantánea en ese momento. El balón tarda un tiempo\(t_{f}=1.4 \mathrm{s}\) en alcanzar la altura\(y_{f}=5.0 \mathrm{m}\). La velocidad a esa altura viene dada por

\[v_{y}=-g t_{f}=-\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(1.4 \mathrm{s})=-1.4 \times 10^{1} \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

Entonces la potencia instantánea en el momento\(t_{f}=1.4 \mathrm{s}\) es

\ [\ begin {alineado}
P^ {g} &=F_ {y} ^ {g} v_ {y} =( -m g)\ izquierda (-g t_ {f}\ derecha) =m g^ {2} t_ {f}\\
& =( 0.2\ mathrm {kg})\ izquierda (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ -2 {}\ derecha) ^ {2} (1.4\ mathrm {s}) =2.7\ times 10^ {1}\ mathrm {W}
\ end {alineado}\ nonumber\]

Si este problema se hiciera simbólicamente, las respuestas dadas en la Ecuación (13.7.11) y la Ecuación (13.7.12) diferirían en un factor de dos; las respuestas se han redondeado a dos cifras significativas.

La potencia instantánea crece linealmente con el tiempo. La gráfica de potencia vs. tiempo se muestra en la Figura 13.8. De la figura, se debe ver que la potencia instantánea en cualquier momento es el doble de la potencia promedio entre t = 0 y ese tiempo.

Figura 13.8 Gráfico de potencia vs tiempo

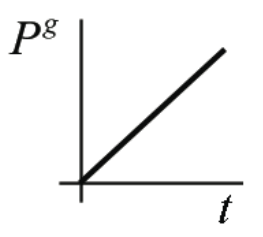
Ejemplo\(\PageIndex{2}\): Power Pushing a Cup

Una persona empuja una taza de masa 0.2 kg a lo largo de una mesa horizontal con una fuerza de magnitud 2.0 N en un ángulo de\(30^{\circ}\) con respecto a la horizontal para una distancia de 0.5 m, como en el Ejemplo 13.4. El coeficiente de fricción entre la mesa y la copa es\(\mu_{k}=0.1\). ¿Cuál es la potencia promedio de la fuerza de empuje? ¿Cuál es la potencia promedio de la fuerza de fricción cinética?

Solución

Utilizaremos los resultados de los Ejemplos 13.4 y 13.7 pero manteniendo cifras extra significativas en los cálculos intermedios. El trabajo realizado por la fuerza de empuje es

\[W^{a}=F_{x}^{a}\left(x_{f}-x_{0}\right)=(1.732 \mathrm{N})(0.50 \mathrm{m})=8.660 \times 10^{-1} \mathrm{J} \nonumber \]

La velocidad final de la copa es\(v_{x, f}=2.860 \mathrm{m} \cdot \mathrm{s}^{-1}\). Asumiendo una aceleración constante, el tiempo durante el cual se empujó la copa es

\[t_{f}=\frac{2\left(x_{f}-x_{0}\right)}{v_{x, f}}=0.3496 \mathrm{s} \nonumber \]

El poder promedio de la fuerza de empuje es entonces, con\(\Delta t=t_{f}\),

\[P_{\text {ave }}^{a}=\frac{\Delta W^{a}}{\Delta t}=\frac{8.660 \times 10^{-1} \mathrm{J}}{0.3496 \mathrm{s}}=2.340 \mathrm{W} \nonumber \]

o 2.3W a dos cifras significativas. El trabajo realizado por la fuerza de fricción es

\ [\ begin {alineado}
W^ {f} &=f_ {\ mathrm {k}}\ izquierda (x_ {f} -x_ {0}\ derecha)\\
&=-\ mu_ {\ mathrm {k}} N\ izquierda (x_ {f} -x_ {0}\ derecha) =-\ izquierda (9.6\ veces 10^ {-2}\ mathrm {N}\ derecha) (0.50\ mathrm {m}) =-\ izquierda (4.8\ veces 10^ {-2}\ mathrm {J}\ derecha)
\ end {alineado}\ nonumber\]

La potencia promedio de la fricción cinética es

\[P_{\text {ave }}^{f}=\frac{\Delta W^{f}}{\Delta t}=\frac{-4.8 \times 10^{-2} \mathrm{J}}{0.3496 \mathrm{s}}=-1.4 \times 10^{-1} \mathrm{W} \nonumber \]

La tasa de cambio temporal de la energía cinética para un cuerpo de masa m que se mueve en la dirección x es

\[\frac{d K}{d t}=\frac{d}{d t}\left(\frac{1}{2} m v_{x}^{2}\right)=m \frac{d v_{x}}{d t} v_{x}=m a_{x} v_{x} \nonumber \]

Por la Segunda Ley de Newton,\(F_{x}=m a_{x}\) y así la Ecuación (13.7.18) se convierte en

\[\frac{d K}{d t}=F_{x} v_{x}=P \nonumber \]

La potencia instantánea entregada al cuerpo es igual a la tasa temporal de cambio de la energía cinética del cuerpo.