13.8: El trabajo y el producto escalar

Introduciremos una operación vectorial, llamada el producto escalar o “producto punto” que toma dos vectores cualesquiera y genera una cantidad escalar (un número). Veremos que el concepto físico de trabajo puede ser descrito matemáticamente por el producto escalar entre los vectores de fuerza y desplazamiento.

Producto Escalar

Dejar\(\overrightarrow{\mathbf{A}}\) y\(\overrightarrow{\mathbf{B}}\) ser dos vectores. Debido a que dos vectores no colineales forman un plano, definimos el ángulo θ para que sea el ángulo entre los vectores\(\overrightarrow{\mathbf{A}}\) y\(\overrightarrow{\mathbf{B}}\) como se muestra en la Figura 13.9. Tenga en cuenta que θ puede variar de 0 a\(\pi\).

Figura 13.9 Geometría escalar del producto.

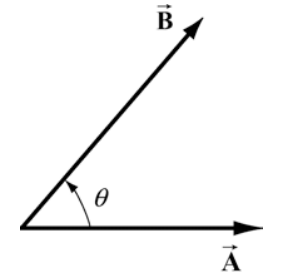
El producto escalar\(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}\) de los vectores\(\overrightarrow{\mathbf{A}}\) y\(\overrightarrow{\mathbf{B}}\) se define como producto de la magnitud de los vectores\(\overrightarrow{\mathbf{A}}\) y\(\overrightarrow{\mathbf{B}}\) con el coseno del ángulo θ entre los dos vectores:

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A B \cos (\theta) \nonumber \]

donde\(A=|\overrightarrow{\mathbf{A}}| \text { and } B=\mid \overrightarrow{\mathbf{B}}\) representan la magnitud de\(\overrightarrow{\mathbf{A}}\) y\(\overrightarrow{\mathbf{B}}\) respectivamente. El producto escalar puede ser positivo, cero o negativo, dependiendo del valor de\(\cos \theta\). El producto escalar es siempre una cantidad escalar.

Por lo tanto, el ángulo formado por dos vectores es

\[\theta=\cos ^{-1}\left(\frac{\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}}{|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}|}\right) \nonumber \]

La magnitud de un vector\(\overrightarrow{\mathbf{A}}\) viene dada por la raíz cuadrada del producto escalar del vector\(\overrightarrow{\mathbf{A}}\) consigo mismo.

\[|\overrightarrow{\mathbf{A}}|=(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})^{1 / 2} \nonumber \]

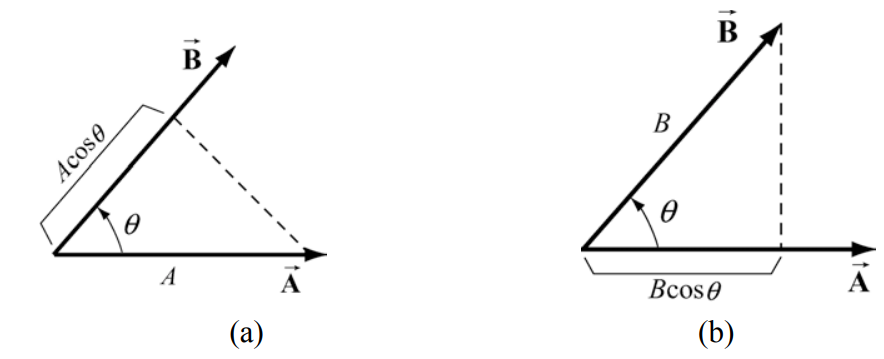
Podemos dar una interpretación geométrica al producto escalar escribiendo la definición como

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=(A \cos (\theta)) B \nonumber \]

En esta formulación, el término Acosθ es la proyección del vector\(\overrightarrow{\mathbf{B}}\) en la dirección del vector\(\overrightarrow{\mathbf{B}}\). Esta proyección se muestra en la Figura 13.10a. Entonces el producto escalar es el producto de la proyección de la longitud de\(\overrightarrow{\mathbf{A}}\) en la dirección de\(\overrightarrow{\mathbf{B}}\) con la longitud de\(\overrightarrow{\mathbf{B}}\). Tenga en cuenta que también podríamos escribir el producto escalar como

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A(B \cos (\theta)) \nonumber \]

Ahora el término\(B \cos (\theta)\) es la proyección del vector\(\overrightarrow{\mathbf{B}}\) en la dirección del vector\(\overrightarrow{\mathbf{A}}\) como se muestra en la Figura 13.10b. Desde esta perspectiva, el producto escalar es el producto de la proyección de la longitud de\(\overrightarrow{\mathbf{B}}\) en la dirección de\(\overrightarrow{\mathbf{A}}\) con la longitud de\(\overrightarrow{\mathbf{A}}\).

Figura 13.10 (a) y (b) Proyección de vectores y el producto escalar

De nuestra definición del producto escalar vemos que el producto escalar de dos vectores que son perpendiculares entre sí es cero ya que el ángulo entre los vectores es\(\pi / 2\) y\(\cos (\pi / 2)=0\).

Podemos calcular el producto escalar entre dos vectores en un sistema de coordenadas cartesianas de la siguiente manera. Considerar dos vectores\(\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}}\) y\(\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}}+B_{y} \hat{\mathbf{j}}+B_{z} \hat{\mathbf{k}}\). Recordemos que

\ [\ begin {array} {l}
\ hat {\ mathbf {i}}\ cdot\ hat {\ mathbf {i}} =\ hat {\ mathbf {j}}\ cdot\ hat {\ mathbf {j}} =\ hat {\ mathbf {k}}\ cdot\ hat {\ mathbf {k}} =1\
\ hat {\ mathbf {i}\ cdot\ sombrero {\ mathbf {j}} =\ sombrero {\ mathbf {j}}\ cdot\ sombrero {\ mathbf {k}} =\ sombrero {\ mathbf {i}}\ cdot\ sombrero {\ mathbf {k}} =0
\ fin {matriz}\ nonumber\]

El producto escalar entre\(\overrightarrow{\mathbf{A}}\) y\(\overrightarrow{\mathbf{B}}\) es entonces

\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z} \nonumber \]

La derivada temporal del producto escalar de dos vectores viene dada por

\ [\ begin {array} {l}
\ frac {d} {d t} (\ overrightarrow {\ mathbf {A}}\ cdot\ overrightarrow {\ mathbf {B}}) =\ frac {d} {d} {d t}\ left (A_ {x} B_ {x} +A_ {y} B_ {y} +A_ {z} B_ {z}\ derecha)\\
=\ frac {d} {d t}\ izquierda (A_ {x}\ derecha) B_ {x} +\ frac {d} {d} {d t}\ izquierda (A_ {y}\ derecha) B_ {y} +\ frac {d} {d} {d t}\ izquierda (A_ {z}\ derecha) B_ {z} +A_ {x}\ frac {d} {d t}\ izquierda (B_ {x}\ derecha) +A_ {y}\ frac {d} {d} {d t}\ izquierda (B_ {y}\ derecha) +A_ {z}\ frac {d} {d t}\ izquierda (B_ {z}\ derecha)\\
=\ izquierda (\ frac {d} {d}\ overtarright fila {\ mathbf {A}}\ derecha)\ cdot\ overrightarrow {\ mathbf {B}} +\ overrightarrow {\ mathbf {A}}\ cdot\ izquierda (\ frac {d} {d} {d t}\ overrightarrow {\ mathbf {B}}\ derecha)
\ end {array}\ nonumber\]

En particular cuando\(\overrightarrow{\mathbf{A}}=\overrightarrow{\mathbf{B}}\), entonces la derivada temporal del cuadrado de la magnitud del vector\(\overrightarrow{\mathbf{A}}\) viene dada por

\[\frac{d}{d t} A^{2}=\frac{d}{d t}(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})=\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{A}} \cdot\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right)=2\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{A}} \nonumber \]

La energía cinética y el producto escalar

Para un objeto sometido a movimiento tridimensional, la velocidad del objeto en componentes cartesianos viene dada por\(\overrightarrow{\mathbf{v}}=v_{x} \hat{\mathbf{i}}+v_{y} \hat{\mathbf{j}}+v_{z} \hat{\mathbf{k}}\). Recordemos que la magnitud de un vector viene dada por la raíz cuadrada del producto escalar del vector consigo mismo,

\[A \equiv|\overrightarrow{\mathbf{A}}| \equiv(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})^{1 / 2}=\left(A_{x}^{2}+A_{y}^{2}+A_{z}^{2}\right)^{1 / 2} \nonumber \]

Por lo tanto, el cuadrado de la magnitud de la velocidad viene dado por la expresión

\[v^{2} \equiv(\overrightarrow{\mathbf{v}} \cdot \overrightarrow{\mathbf{v}})=v_{x}^{2}+v_{y}^{2}+v_{z}^{2} \nonumber \]

De ahí que la energía cinética del objeto viene dada por

\[K=\frac{1}{2} m(\overrightarrow{\mathbf{v}} \cdot \overrightarrow{\mathbf{v}})=\frac{1}{2} m\left(v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\right) \nonumber \]

El trabajo y el producto escalar

El trabajo es un ejemplo físico importante de la operación matemática de tomar el producto escalar entre dos vectores. Recordemos que cuando una fuerza constante actúa sobre un cuerpo y el punto de aplicación de la fuerza sufre un desplazamiento a lo largo del eje x, solo la componente de la fuerza a lo largo de esa dirección contribuye al trabajo,

\[W=F_{x} \Delta x \nonumber \]

Supongamos que estamos tirando de un cuerpo a lo largo de una superficie horizontal con una fuerza\(\overrightarrow{\mathbf{F}}\). Elija coordenadas de tal manera que la dirección horizontal sea el eje x y la fuerza\(\overrightarrow{\mathbf{F}}\) forme un ángulo\(\beta\) con la dirección x positiva. En la Figura 13.11 se muestra el vector de fuerza\(\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}\) y el vector de desplazamiento del punto de aplicación de la fuerza\(\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}\). Tenga en cuenta que\(\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}\) es el componente del desplazamiento y por lo tanto puede ser mayor, igual o menor que cero (pero se muestra como mayor que cero en la figura para mayor claridad). El producto escalar entre el vector de fuerza\(\overrightarrow{\mathbf{F}}\) y el vector de desplazamiento\(\Delta \overrightarrow{\mathbf{x}}\) es

\[\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}}=\left(F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}\right) \cdot(\Delta x \hat{\mathbf{i}})=F_{x} \Delta x \nonumber \]

Figura 13.11 Vectores de fuerza y desplazamiento

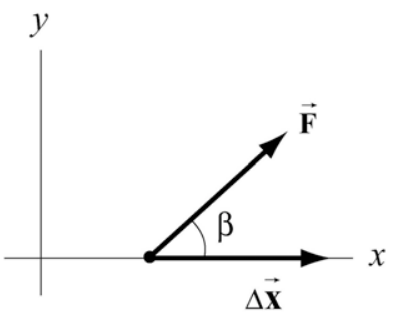
El trabajo realizado por la fuerza es entonces

\[\Delta W=\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}} \nonumber \]

En general, el ángulo\(\beta\) toma valores dentro del rango\(-\pi \leq \beta \leq \pi\) (en la Figura 13.11,\(0 \leq \beta \leq \pi / 2\)). Debido a que el componente x de la fuerza es\(F_{x}=F \cos (\beta)\) donde\(F=|\overrightarrow{\mathbf{F}}|\) denota la magnitud de\(\overrightarrow{\mathbf{F}}\), el trabajo realizado por la fuerza es

\[W=\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}}=(F \cos (\beta)) \Delta x \nonumber \]

Ejemplo 13.10 Objeto Deslizándose por un Plano Inclinado

Un objeto de masa m = 4.0 kg, partiendo del reposo, se desliza hacia abajo por un plano inclinado de longitud l = 3.0 m. El plano está inclinado por un ángulo con respecto\(\theta=30^{\circ}\) al suelo. El coeficiente de fricción cinética es\(\mu_{k}=0.2\) (a) ¿Cuál es el trabajo realizado por cada una de las tres fuerzas mientras el objeto se desliza por el plano inclinado? b) Por cada fuerza, ¿el trabajo realizado por la fuerza es positivo o negativo? c) ¿Cuál es la suma del trabajo realizado por las tres fuerzas? ¿Esto es positivo o negativo?

Solución: (a) y (b) Elija un sistema de coordenadas con el origen en la parte superior del plano inclinado y la dirección x positiva apuntando hacia abajo del plano inclinado, y la dirección y positiva apuntando hacia la parte superior derecha como se muestra en la Figura 13.12. Mientras el objeto se desliza por el plano inclinado, tres fuerzas uniformes actúan sobre el objeto, la fuerza gravitacional que apunta hacia abajo y tiene magnitud\(F_{g}=m g\), la fuerza normal N que es perpendicular a la superficie del plano inclinado, y la fuerza de fricción que se opone al movimiento y es igual en magnitud a\(f_{k}=\mu_{k} N\). En la Figura 13.13 se muestra un diagrama de fuerza sobre el objeto.

Figura 13.12 Sistema de coordenadas para el objeto que se desliza por el plano inclinado

Figura 13.13 Diagrama de fuerza de cuerpo libre para objeto

Para poder calcular el trabajo necesitamos determinar qué fuerzas tienen un componente en la dirección del desplazamiento. Solo la componente de la fuerza gravitacional a lo largo de la dirección x positiva\(F_{g x}=m g \sin \theta\) y la fuerza de fricción se dirigen a lo largo del desplazamiento y por lo tanto contribuyen al trabajo. Necesitamos usar la Segunda Ley de Newton para determinar las magnitudes de la fuerza normal. Debido a que el objeto está restringido a moverse a lo largo de la dirección x positiva,\(a_{y}=0\), La Segunda Ley de Newton en la\(\hat{\mathbf{j}}\) dirección -dirección\(N-m g \cos \theta=0\). Por lo tanto\(N=m g \cos \theta\) y la magnitud de la fuerza de fricción es\(f_{k}=\mu_{k} m g \cos \theta\).

Con nuestra elección del sistema de coordenadas con el origen en la parte superior del plano inclinado y la dirección x positiva apuntando hacia abajo del plano inclinado, el desplazamiento del objeto viene dado por el vector\(\Delta \overrightarrow{\mathbf{r}}=\Delta x \hat{\mathbf{i}}\) (Figura 13.14).

Figura 13.14 Vectores de fuerza y vector de desplazamiento para objeto

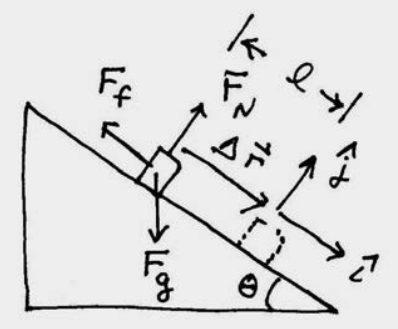
La descomposición vectorial de las tres fuerzas son\(\overrightarrow{\mathbf{F}}^{g}=m g \sin \theta \hat{\mathbf{i}}-m g \cos \theta \hat{\mathbf{j}}\),\(\overrightarrow{\mathbf{F}}^{f}=-\mu_{k} m g \cos \theta \hat{\mathbf{i}}\), y\(\overrightarrow{\mathbf{F}}^{N}=m g \cos \theta \hat{\mathbf{j}}\). El trabajo realizado por la fuerza normal es cero porque la fuerza normal es perpendicular al desplazamiento

\[W^{N}=\overrightarrow{\mathbf{F}}^{N} \cdot \Delta \overrightarrow{\mathbf{r}}=m g \cos \theta \hat{\mathbf{j}} \cdot l \hat{\mathbf{i}}=0 \nonumber \]

Entonces el trabajo realizado por la fuerza de fricción es negativo y dado por

\[W^{f}=\overrightarrow{\mathbf{F}}^{f} \cdot \Delta \overrightarrow{\mathbf{r}}=-\mu_{k} m g \cos \theta \hat{\mathbf{i}} \cdot l \hat{\mathbf{i}}=-\mu_{k} m g \cos \theta l<0 \nonumber \]

Sustituir en los valores apropiados rendimientos

\[W^{f}=-\mu_{k} m g \cos \theta l=-(0.2)(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(3.0 \mathrm{m})\left(\cos \left(30^{\circ}\right)(3.0 \mathrm{m})=-20.4 \mathrm{J}\right. \nonumber \]

El trabajo realizado por la fuerza gravitacional es positivo y dado por

\[W^{g}=\overrightarrow{\mathbf{F}}^{g} \cdot \Delta \overrightarrow{\mathbf{r}}=(m g \sin \theta \hat{\mathbf{i}}-m g \cos \theta \hat{\mathbf{j}}) \cdot l \hat{\mathbf{i}}=m g l \sin \theta>0 \nonumber \]

Sustituir en los valores apropiados rendimientos

\[W^{g}=m g l \sin \theta=(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(3.0 \mathrm{m})\left(\sin \left(30^{\circ}\right)=58.8 \mathrm{J}\right. \nonumber \]

c) La suma escalar del trabajo realizado por las tres fuerzas es entonces

\ [\ begin {array} {l}
W=W^ {g} +W^ {f} =m g l\ izquierda (\ sin\ theta-\ mu_ {k}\ cos\ theta\ derecha)\\
W =( 4.0\ mathrm {kg})\ izquierda (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ derecha) (3.0\ mathrm {m})\ izquierda (\ sin\ izquierda (30^ {\ circ}\ derecha) - (0.2)\ izquierda (\ cos\ izquierda (30^ {\ circ}\ derecha)\ derecha) =38.4\ mathrm {J}. \ derecho.
\ end {array}\ nonumber\]