25.2: Órbitas Planetarias

Comenzamos ahora un estudio del Problema Kepler. Determinaremos la ecuación de movimiento para los movimientos de dos cuerpos que interactúan a través de una fuerza gravitacional (problema de dos cuerpos) utilizando métodos de fuerza y leyes de conservación.

Reducir el problema de dos cuerpos en un problema de un solo cuerpo

Comenzaremos por mostrar cómo el movimiento de dos cuerpos que interactúan a través de una fuerza gravitacional (problema de dos cuerpos) es matemáticamente equivalente al movimiento de un solo cuerpo sobre el que actúa una fuerza gravitacional central externa, donde la masa del solo cuerpo es la masa reducida\(\mu\),

\[\frac{1}{\mu}=\frac{1}{m_{1}}+\frac{1}{m_{2}} \Rightarrow \mu=\frac{m_{1} m_{2}}{m_{1}+m_{2}} \nonumber \]

Una vez que resolvemos el movimiento del cuerpo reducido en este problema equivalente de un solo cuerpo, entonces podemos volver al problema real de dos cuerpos y resolver el movimiento real de los dos cuerpos originales. La masa reducida se introdujo en el Capítulo 13 Apéndice A de estas notas. Ese apéndice utilizó una notación similar pero ligeramente diferente a la utilizada en este capítulo.

Considere la interacción gravitacional entre dos cuerpos con masas m y como 1 m2 que se muestra en la Figura 25.1.

Figura 25.1 Fuerza gravitacional entre dos cuerpos

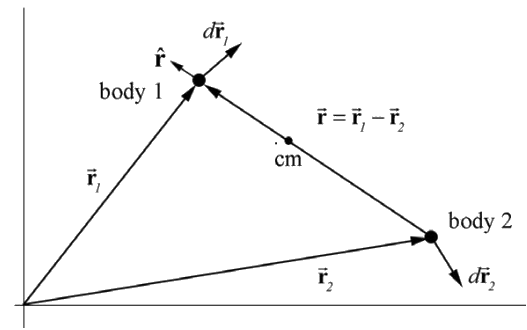
Elija un sistema de coordenadas con elección de origen de tal manera que el cuerpo 1 tenga posición\(\overrightarrow{\mathbf{r}}_{1}\) y el cuerpo 2 tenga posición\(\overrightarrow{\mathbf{r}}_{2}\) (Figura 25.2). El vector de posición relativa\(\overrightarrow{\mathbf{r}}\) que apunta desde el cuerpo 2 al cuerpo 1 es\(\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{1}-\overrightarrow{\mathbf{r}}_{2}\) Denotamos la magnitud de\(\overrightarrow{\mathbf{r}} \text { by }|\overrightarrow{\mathbf{r}}|=r\), donde r es la distancia entre los cuerpos, y\(\hat{\mathbf{r}}\) es el vector unitario apuntando desde el cuerpo 2 al cuerpo 1, de manera que\(\overrightarrow{\mathbf{r}}=r \hat{\mathbf{r}}\).

Figura 25.2 Sistema de coordenadas para el problema de dos cuerpos

La fuerza sobre el cuerpo 1 (debido a la interacción de los dos cuerpos) puede ser descrita por la Ley Universal de Gravitación de Newton

\[\overrightarrow{\mathbf{F}}_{2,1}=-F_{2,1} \hat{\mathbf{r}}=-G \frac{m_{1} m_{2}}{r^{2}} \hat{\mathbf{r}} \nonumber \]

Recordemos que la Tercera Ley de Newton requiere que la fuerza sobre el cuerpo 2 sea igual en magnitud y opuesta en dirección a la fuerza sobre el cuerpo 1,

\[\overrightarrow{\mathbf{F}}_{1,2}=-\overrightarrow{\mathbf{F}}_{2,1} \nonumber \]

La Segunda Ley de Newton se puede aplicar individualmente a los dos cuerpos:

\ [\ begin {array} {l}
\ overrightarrow {\ mathbf {F}} _ {2,1} =m_ {1}\ frac {d^ {2}\ overrightarrow {\ mathbf {r}} _ {1}} {d t^ {2}}\
\ overrightarrow {\ mathbf {F}} _ {1,2} =m_ {2} frac {d^ {2}\ overrightarrow {\ mathbf {r}} _ {2}} {d t^ {2}}
\ end {array}\ nonumber\]

Dividiendo por la masa en cada una de las Ecuaciones (25.2.4) y (25.2.5) rinde

\[\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}} \nonumber \]

\[\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}} \nonumber \]

Restar la expresión en la Ecuación (25.2.7) de la de la Ecuación (25.2.6) rinde

\[\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}-\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}}-\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}}{d t^{2}} \nonumber \]

Usando la Tercera Ley de Newton, la Ecuación (25.2.3), la Ecuación (25.2.8) se convierte

\[\overrightarrow{\mathbf{F}}_{2,1}\left(\frac{1}{m_{1}}+\frac{1}{m_{2}}\right)=\frac{d^{2} \overrightarrow{\mathbf{r}}}{d t^{2}} \nonumber \]

Usando la masa reducida µ, como se define en la Ecuación (25.2.1), la Ecuación (25.2.9) se convierte

\ [\ begin {array} {l}
\ frac {\ overrightarrow {\ mathbf {F}} _ {2,1}} {\ mu} =\ frac {d^ {2}\ overrightarrow {\ mathbf {r}}} {d t^ {2}}\
\ overrightarrow {\ mathbf {F}} _ {2,1} =\ mu\ frac d^ {2}\ overrightarrow {\ mathbf {r}}} {d t^ {2}}
\ end {array}\ nonumber\]

donde\(\overrightarrow{\mathbf{F}}_{2,1}\) viene dada por la Ecuación (25.2.2).

Nuestro resultado tiene una interpretación especial utilizando la Segunda Ley de Newton. Dejar\(\mu\) ser la masa de un solo cuerpo con vector de posición\(\overrightarrow{\mathbf{r}}=r \hat{\mathbf{r}}\) con respecto a un origen O, donde\(\hat{\mathbf{r}}\) está el vector unitario apuntando desde el origen O al solo cuerpo. Entonces la ecuación de movimiento, Ecuación (25.2.10), implica que el único cuerpo de masa\(\mu\) se encuentra bajo la influencia de una fuerza gravitacional atractiva que apunta hacia el origen. Entonces, el problema gravitacional original de dos cuerpos ahora se ha reducido a un problema equivalente de un solo cuerpo, involucrando a un solo cuerpo con masa\(\mu\) bajo la influencia de una fuerza central\(\overrightarrow{\mathbf{F}}^{G}=-\mathrm{F}_{2,1} \hat{\mathbf{r}}\) Tenga en cuenta que en esta reformulación, no hay cuerpo localizado en el punto central (el origen O). El parámetro r en el problema de dos cuerpos es la distancia relativa entre los dos cuerpos originales, mientras que el mismo parámetro r en el problema de un solo cuerpo es la distancia entre el cuerpo único y el punto central. Esta reducción generaliza a todas las fuerzas centrales.