5.1: Un oscilador armónico obedece a la ley de Hooke
- Page ID
- 80230
El movimiento de dos átomos en una molécula diatómica se puede separar en movimientos traslacionales, vibracionales y rotacionales. Tanto los movimientos de rotación como los movimientos vibracionales son movimientos internos que no cambian el centro de masa de la molécula (Figura 5.1.1 ), que se describe por el movimiento traslacional. Los movimientos de traslación cuántica se pueden modelar con la partícula en un modelo de caja discutido anteriormente y la rotación y la vibración se pueden modelar a través de los modelos de rotor rígido y oscilador armónico, respectivamente.
Antes de adentrarnos en el oscilador armónico mecánico cuántico, introduciremos el oscilador armónico clásico (es decir, involucrando la mecánica clásica) para construir una intuición que extenderemos al mundo cuántico. Se necesita una descripción clásica de la vibración de una molécula diatómica porque la descripción mecánica cuántica comienza con la sustitución de la energía clásica con el operador hamiltoniano en la ecuación de Schrödinger. También es interesante comparar y contrastar la descripción clásica con la imagen mecánica cuántica.
El oscilador armónico clásico
Los osciladores armónicos simples sobre un mínimo de energía potencial pueden considerarse como una bola rodando sin fricción en un plato curvo o un péndulo balanceándose sin fricción de un lado a otro (Figura 5.1.2 ). Las fuerzas restauradoras son precisamente las mismas en cualquier dirección horizontal.
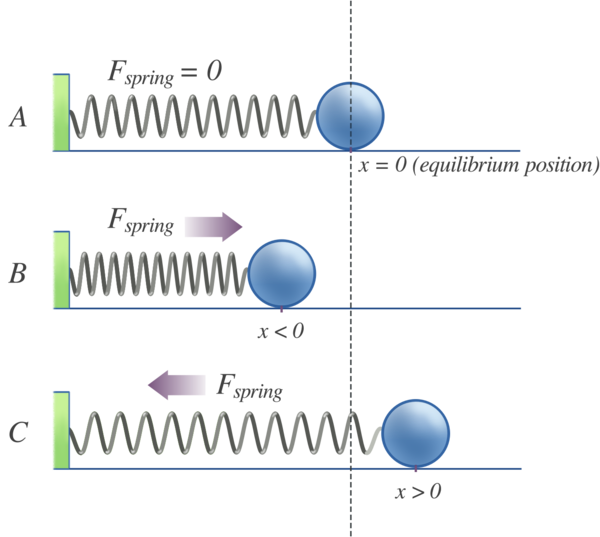
Si consideramos que el vínculo se comporta como una masa en un resorte (Figura 5.1.2 ), entonces esta fuerza restauradora (\(F\)) es proporcional al desplazamiento (\(x\)) desde la longitud de equilibrio (\(x_o\)) - esta es la Ley de Hooke:
\[ F = - kx \label {5.1.2} \]
donde\(k\) está la constante de la fuerza. La Ley de Hooke dice que la fuerza es proporcional a, pero en dirección opuesta a, el desplazamiento (\(x\)). La constante de fuerza refleja la rigidez del resorte. La idea incorporada a la aplicación de la Ley de Hooke a una molécula diatómica es que cuando los átomos se alejan de sus posiciones de equilibrio, se produce una fuerza restauradora que aumenta proporcionalmente con el desplazamiento del equilibrio. La energía potencial para dicho sistema aumenta cuadráticamente con el desplazamiento.
\[ V (x) = \dfrac {1}{2} k x^2 \label {5.1.3} \]
La Ley de Hooke o el potencial armónico (es decir cuadrático) dado por la ecuación\(\ref{5.1.3}\) es una excelente aproximación para las oscilaciones vibracionales de las moléculas. La magnitud de la constante de fuerza\(k\) depende de la naturaleza del enlace químico en los sistemas moleculares, así como depende de la naturaleza del resorte en los sistemas mecánicos. Cuanto mayor es la constante de fuerza, más rígido es el resorte o más rígido es el enlace. Dado que es la distribución de electrones entre los dos núcleos cargados positivamente lo que los mantiene unidos, un doble enlace con más electrones tiene una constante de fuerza mayor que un enlace simple, y los núcleos se mantienen unidos más fuertemente.
Un enlace rígido con una gran constante de fuerza no es necesariamente un enlace fuerte con una gran energía de disociación. Un oscilador armónico no tiene energía de disociación ya que NO PUEDE romperse; siempre hay una fuerza restauradora para mantener unida la molécula. Esta es una de las muchas deficiencias en el uso del modelo de oscilador armónico para describir las vibraciones moleculares.
¿
Es posible que haya cuestionado la aplicabilidad del modelo de oscilador armónico que involucra una masa móvil unida a una pared fija a través de un resorte como en la Figura 5.1.2 para la vibración de una molécula diatómica con dos masas móviles como en la Figura 5.1.1 . Resultó que los dos son matemáticamente iguales con el movimiento de vibración interna descrito por una sola partícula reducida con una masa reducida\(μ\).
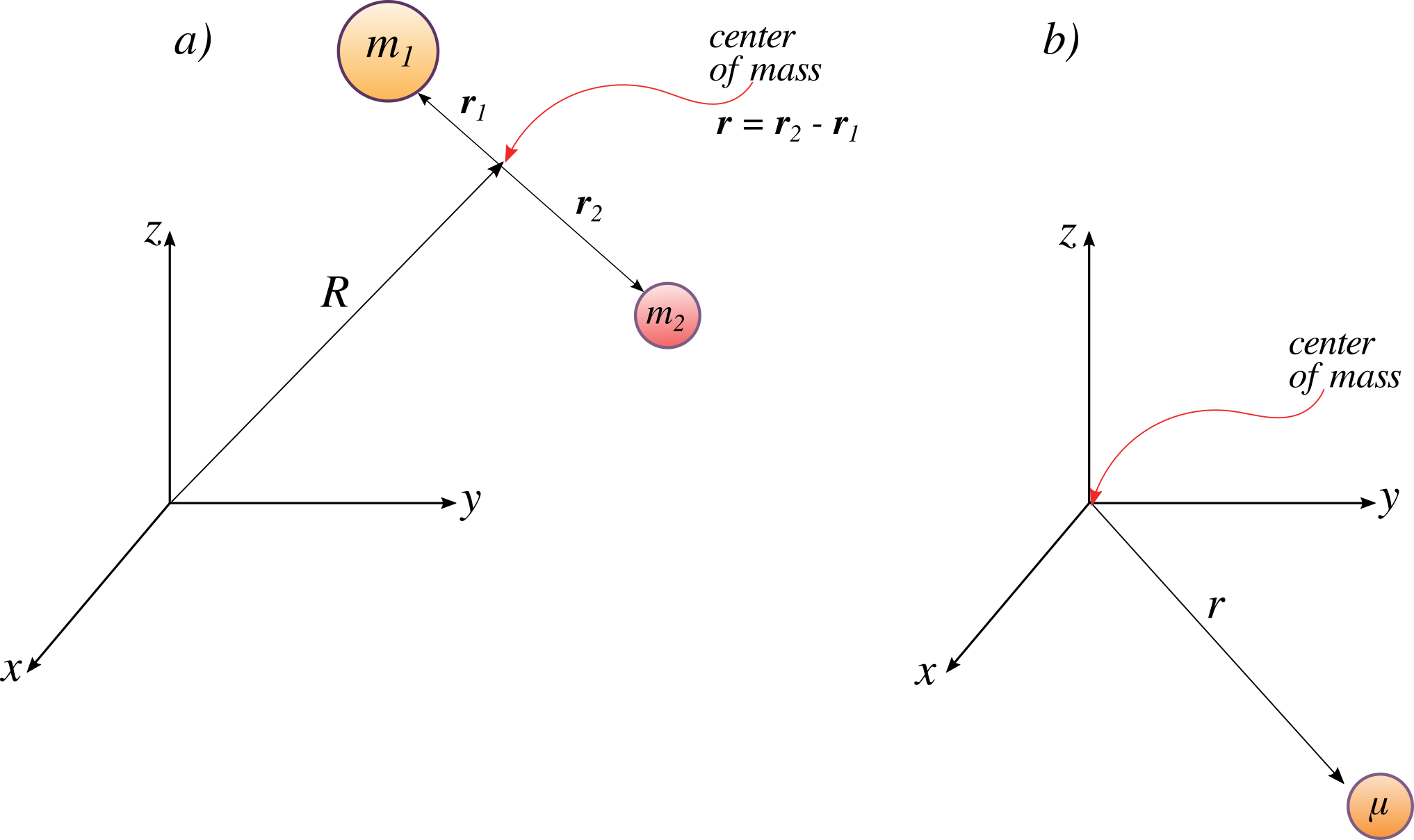
Para una molécula diatómica, Figura 5.1.3 , el vector\(\vec{r}\) corresponde al eje internuclear. La magnitud o longitud de\(r\) es la longitud del enlace, y la orientación de\(r\) en el espacio da la orientación del eje internuclear en el espacio. Los cambios en la orientación corresponden a la rotación de la molécula, y los cambios en la longitud corresponden a la vibración. El cambio en la longitud del enlace a partir de la longitud del enlace de equilibrio es la coordenada vibracional para una molécula diatómica.
- Mostrar que menos la primera derivada de la función de energía potencial armónica en la Ecuación\(\ref{5.1.3}\) con respecto a\(x\) es la fuerza de la Ley de Hooke en la Ecuación\ ref {5.1.2}.
- Demostrar que la segunda derivada es la constante de fuerza,\(k\).
- ¿A qué valor de la energía potencial\(x\) es mínima; ¿a qué valor de\(x\) es la fuerza cero?
- Croquis gráficos para comparar la energía potencial y la fuerza para un sistema con una constante de fuerza grande a uno con una constante de fuerza pequeña.
Solución a
La Ley de Hooke para un resorte implica que la fuerza aplicada sobre un resorte\(F\) es igual a la constante de fuerza,\(-k\) multiplicada por la distancia comprimida o estirada,\(x\) (Ecuación\ ref {5.1.2}). El derivado de\(V(x) = 0.5 k x^2\) es
\[V'(x) = (2)\left(\dfrac{1}{2}\right)kx = kx. \nonumber \]
Lo negativo de esto es\(-V'(x) = -kx\) que es exactamente igual a la Ley de Hooke.
Solución b
La segunda derivada
\[V"(x) = \dfrac{d}{dx} kx = k \nonumber \]
Así, la segunda derivada de esta ecuación para la energía potencial es igual a la constante de fuerza,\(k\).
Solución c
Para encontrar la energía potencial mínima, es más fácil establecer la primera derivada igual a cero y resolver para x Cuando\(V'(x) = kx = 0\) entonces x debe ser igual a cero. Así, la energía potencial mínima es cuando x=0. Conectando esto a la Ley de Hooke,\(F(0) = -k(0) = 0\) así que este es también el valor para x cuando la fuerza es cero.
Solución d
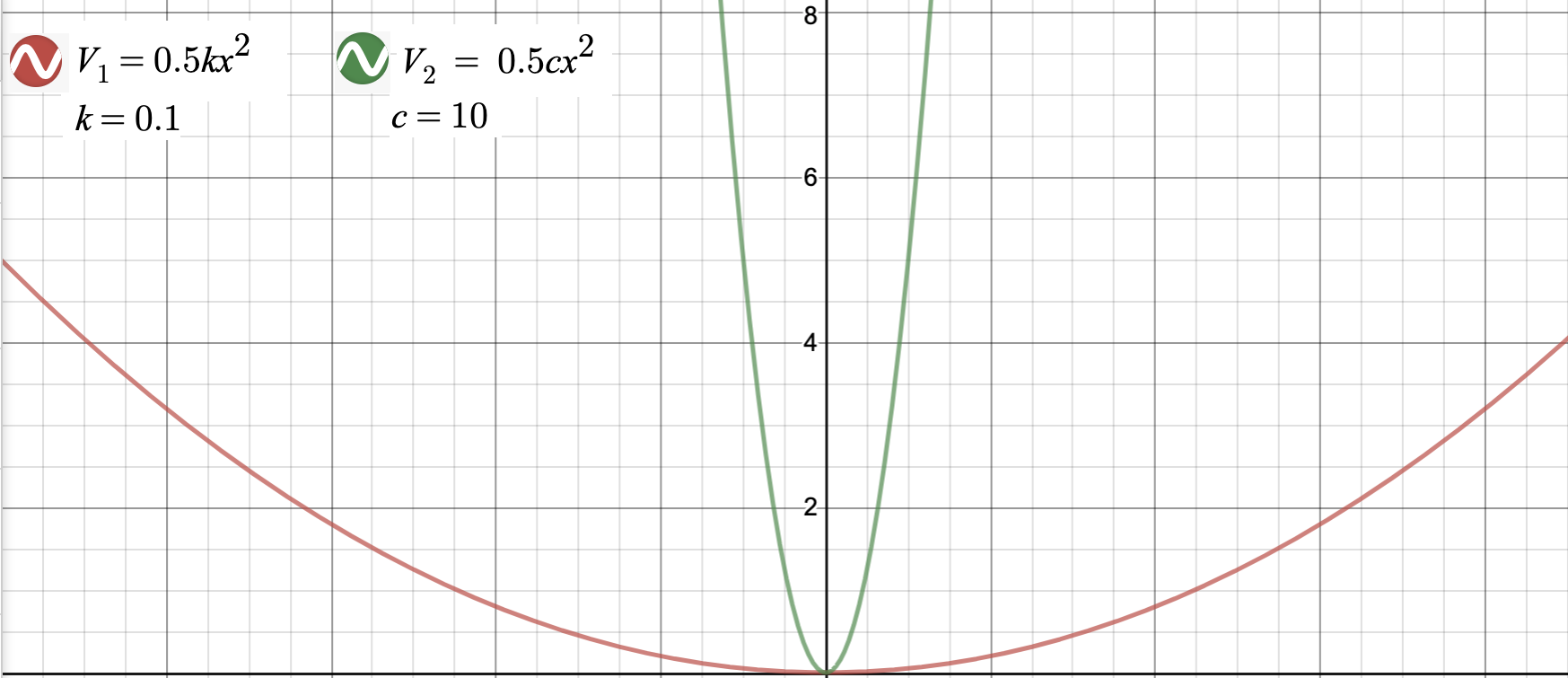
La constante de fuerza tiene un efecto drástico tanto en la energía potencial como en la fuerza. Un sistema con una constante de fuerza grande requiere un cambio mínimo\(x\) para tener un cambio drástico en la energía o fuerza potencial, mientras que un sistema con una constante de fuerza pequeña es el fenómeno exactamente opuesto.
Resolviendo el modelo de oscilador armónico
La ecuación clásica de movimiento para un oscilador armónico simple unidimensional con una partícula de masa\(m\) unida a un resorte que tiene constante de resorte\(k\) es
\[ m \dfrac{d^2x(t)}{dt^2} = -kx(t) \label{5.1.4a} \]
que se puede reescribir en el formulario estándar:
\[ \dfrac{d^2x(t)}{dt^2} + \dfrac{k}{m}x(t) = 0 \label{5.1.4b} \]
\(\ref{5.1.4a}\)La ecuación es una ecuación diferencial lineal de segundo orden que puede resolverse mediante el método estándar de factorización e integración. La solución resultante a la ecuación\(\ref{5.1.4a}\) es
\[ x(t) = x_o \sin (\omega t + \phi) \label{5.1.5} \]
con
\[\omega = \sqrt{\dfrac{k}{m}} \label{5.1.6} \]
y el impulso\(\) tiene dependencia del tiempo
\[\begin{align*} p &= mv \\[4pt] &=mx_o \omega \cos (\omega t + \phi) \label{5.1.7} \end{align*} \]
La Figura 5.1.4 muestra el desplazamiento del enlace desde su longitud de equilibrio en función del tiempo. Tal movimiento se llama armónico.
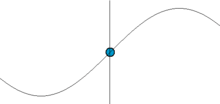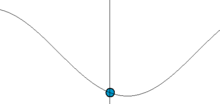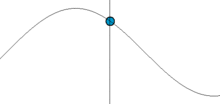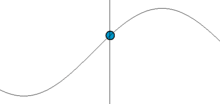
Sustituir las siguientes funciones en Ecuación\(\ref{5.1.4b}\) para demostrar que ambas son posibles soluciones a la ecuación clásica del movimiento.
- \(x(t) = x_0 e^{i \omega t} \)
- \(x(t) = x_0 e^{-i \omega t}\)
donde
\[ \omega = \sqrt {\dfrac {k}{m}} \nonumber \]
Tenga en cuenta que el símbolo griego\(\omega\) para frecuencia representa la frecuencia angular\(2π\nu\).
Solución a
Esto requiere simplemente colocar la función dada\(x(t) = x_0 e^{i \omega t} \) en Ecuación\(\ref{5.1.4b}\).
\[ \begin{align*} \frac{d^2 x(t) }{dt^2} + \frac{k}{m} x(t) &= 0 \\[4pt] \frac{d^2 }{dt^2} \left( x_o e^{i \omega t} \right)+ \frac{k}{m}x_o e^{i \omega t} &= 0\\[4pt] x_o \frac{d^2 }{dt^2} \left( e^{i \omega t} \right)+ \frac{k}{m}x_o e^{i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 \left( e^{i \omega t} \right)+ \frac{k}{m}x_o e^{i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 e^{i \omega t} + \frac{k}{m}x_o e^{i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 + \frac{k}{m}x_o &= 0 \\[4pt] -x_o \frac{k}{m}+ \frac{k}{m}x_o = 0 \; \textrm{ with } \; \omega &= \sqrt{\frac{k}{m}} \end{align*} \nonumber \]
Solución b
Esto requiere simplemente colocar la función dada\(x(t) = x_0 e^{-i \omega t}\) en Ecuación\(\ref{5.1.4b}\).
\[ \begin{align*} \frac{d^2 x(t) }{dt^2} + \frac{k}{m} x(t) &= 0 \\[4pt] \frac{d^2 }{dt^2} \left( x_o e^{-i \omega t} \right)+ \frac{k}{m}x_o e^{-i \omega t}& = 0 \\[4pt] x_o \frac{d^2 }{dt^2} \left( e^{-i \omega t} \right)+ \frac{k}{m}x_o e^{-i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 \left( e^{-i \omega t} \right)+ \frac{k}{m}x_o e^{-i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 e^{-i \omega t} + \frac{k}{m}x_o e^{-i \omega t}& = 0\\[4pt] x_o i^2 \omega^2 + \frac{k}{m}x_o &= 0 \\[4pt] -x_o \frac{k}{m}+ \frac{k}{m}x_o = 0 \; \textrm{ with } \; \omega &= \sqrt{\frac{k}{m}} \end{align*} \nonumber \]
Demostrar que las funciones seno y coseno también son soluciones a la Ecuación\(\ref{5.1.4b}\).
- Contestar
-
Usando Ecuación\(\ref{5.1.4b}\)
\[\frac{d^2x(t)}{dt^2} +\frac{k}{m}x(t)=0 \nonumber \]
con\(\omega =\sqrt{\frac{k}{m}}\).
Para
\[\begin{align*} x(t)=x_{o} \sin(\omega t+\phi) \end{align*} \nonumber \]
Toma la segunda derivada de\(x(t)\)
\[\begin{align*} \frac{d^2x(t)}{dt} &=-\omega^2x_{o}\sin(\omega t+\phi) \\[4pt] &= \omega^2 x_{o}\sin(\omega t+\phi) \\[4pt] &=-\frac{k}{m}x_{o} \sin \left(\sqrt{\frac{k}{m}}t+\phi \right) \end{align*} \nonumber \]
Plug in\(x(t)\) y la segunda derivada de\(x(t)\) en Ecuación\(\ref{5.1.4b}\)
\[\begin{align*} -\frac{k}{m}x_{o}\sin \left(\sqrt{ \frac{k}{m}} t + \phi \right) + \frac{k}{m} x_{o} \sin \left(\sqrt{\frac{k}{m}} t + \phi \right) =0 \end{align*} \nonumber \]
Por lo tanto, la ecuación sinusoidal es una solución a la Ecuación\(\ref{5.1.4b}\)
Hacemos lo mismo para la función coseno
\[x(t)=x_{o}\cos(\omega t + \phi) \nonumber \]
Toma la segunda derivada de\(x(t)\)
\[ \begin{align*} \frac{d^2x(t)}{dt} &=-\omega^2x_{o}\cos(\omega t + \phi) \\[4pt] &= -\omega^2x_{o}\cos( \omega t +\phi) \\[4pt] &=-\frac{k}{m} x_{o} \cos\left( \sqrt{\frac{k}{m}} t + \phi \right ) \end{align*} \nonumber \]
Plug in\(x(t)\) y la segunda derivada de\(x(t)\) en Ecuación\(\ref{5.1.4b}\)
\[\begin{align*} -\frac{k}{m}x_{o} \cos\left( \sqrt{\frac{k}{m}} t + \phi \right) + \frac{k}{m}x_{o} \cos\left( \sqrt{\frac{k}{m}}t + \phi \right)=0 \end{align*} \nonumber \]
La ecuación coseno es también una solución a la Ecuación\(\ref{5.1.4b}\).
Identificar qué sucede con la frecuencia del movimiento a medida que aumenta la constante de fuerza en un caso y a medida que aumenta la masa en otro caso. Si la constante de fuerza se incrementa 9 veces y la masa se incrementa en 4 veces, ¿en qué factor cambia la frecuencia?
- Contestar
-
Esta es una sencilla aplicación de la Ecuación\ ref {5.1.6}. A medida que aumenta la constante de fuerza, la frecuencia del movimiento aumenta, mientras que a medida que aumenta la masa, la frecuencia del movimiento disminuye. Si la constante de fuerza aumentó 9 veces y la masa aumentó 4 veces,
\[ω=\sqrt{\dfrac{9k}{4m}}= \dfrac{3}{2} \left(\dfrac{k}{m}\right) \nonumber \]
Toda la frecuencia de movimiento aumentaría en un factor de 3/2.
Energías del oscilador armónico
La energía de la vibración es la suma de la energía cinética y la energía potencial. El momento asociado con el oscilador armónico es
\[p = m \dfrac {dx}{dt} \label {5.1.8} \]
por lo que combinando Ecuaciones\ ref {5.1.8} y\ ref {5.1.3}, la energía total se puede escribir como
\[ \begin{align} E &= T + V \\[4pt] &= \dfrac {p^2}{2 m} + \dfrac {k}{2} x^2 \label {5.1.9} \end{align} \]
La energía total del oscilador armónico es igual a la energía potencial máxima almacenada en el resorte cuando\(x = \pm A\), llamada los puntos de inflexión (Figura 5.1.5 ). La energía total (Ecuación\(\ref{5.1.9}\)) se desplaza continuamente entre la energía potencial almacenada en la primavera y la energía cinética de la masa.
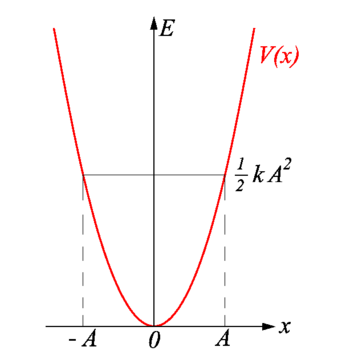
El movimiento de un oscilador clásico se limita a la región donde su energía cinética es no negativa, que es lo que dice la relación energética Ecuación\ ref {5.1.9}. Físicamente, significa que un oscilador clásico nunca se puede encontrar más allá de sus puntos de inflexión, y su energía depende únicamente de cuán lejos estén los puntos de inflexión de su posición de equilibrio. La energía de un oscilador clásico cambia de manera continua. La energía más baja que puede tener un oscilador clásico es cero, lo que corresponde a una situación en la que un objeto está en reposo en su posición de equilibrio. El estado de energía cero de un oscilador clásico simplemente significa que no hay oscilaciones ni ningún movimiento en absoluto (una partícula clásica que se encuentra en la parte inferior del pozo potencial en la Figura 5.1.5 ). Cuando un objeto oscila, por grande o pequeña que sea su energía, pasa el tiempo más largo cerca de los puntos de inflexión, porque aquí es donde ralentiza e invierte su dirección de movimiento. Por lo tanto, la probabilidad de encontrar un oscilador clásico entre los puntos de inflexión es mayor cerca de los puntos de inflexión y más baja en la posición de equilibrio. (Obsérvese que esto no es una declaración de preferencia del objeto para ir a bajar la energía. Es una declaración sobre la rapidez con la que el objeto se mueve a través de diversas regiones.)
- ¿Qué pasa con la frecuencia de la oscilación a medida que la vibración se excita con cada vez más energía?
- ¿Qué sucede con la amplitud máxima de la vibración ya que se excita con cada vez más energía?
Solución
a. Frecuencia
La energía del oscilador armónico se puede escribir como
\[E_{v}=h v\left(v+\dfrac{1}{2}\right) \nonumber \]
y la frecuencia de oscilación es\(\omega=\sqrt{\frac{k}{m}}\). Observe que la frecuencia depende únicamente de la rigidez (\(k\)) y de la masa reducida (\(\mu\)) del oscilador y no de la energía. De ahí que aumentar la energía de las vibraciones no afecta su frecuencia.
b. Amplitud
Los términos cinéticos y potenciales para la energía del oscilador armónico se pueden escribir como
\[\begin{align*} E &=K+V \\[4pt] &=\frac{1}{2} m \omega^{2} A^{2} \sin ^{2} \omega t+\frac{1}{2} k A^2 \cos^2 \omega t \end{align*} \nonumber \]
con\(\omega=\sqrt{\frac{k}{m}}\) tan
\[\begin{align*} E &=\frac{1}{2} k A^{2}\left(\sin ^{2} \omega t+\cos^2 \omega t\right) \\[4pt] &= \frac{1}{2} k A^2 \end{align*} \nonumber \]
La amplitud máxima de la vibración aumentará a medida que aumente la energía.
Si una vibración molecular se excita por colisión con otra molécula y se le da una energía total\(E_{hit}\) como resultado, ¿cuál es la amplitud máxima de la oscilación? ¿Hay alguna restricción en la magnitud de la energía que se pueda introducir?
- Contestar
-
La ecuación que define la energía de una vibración molecular puede aproximarse es:
\[E_{h i t}=T+V=\frac{p^{2}}{2 m}+\frac{k}{2} x \nonumber \]
La amplitud máxima de un oscilador armónico es igual a x cuando el término de energía cinética de la energía total es igual a cero
\[E_{hit}=\frac{k}{2}x \nonumber \]
Resolver para x da la amplitud máxima:
\[x=\sqrt{\frac{2}{k} E_{h i t}} \nonumber \]
La restricción para la energía que se puede introducir no puede ser mayor que la energía requerida para romper el enlace entre los átomos.
Colaboradores y Atribuciones
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski

