4.10: Colisiones entre moléculas de gas Coordenadas de velocidad relativa

La presión de un gas depende de la frecuencia con la que las moléculas chocan con la pared de su contenedor. La velocidad a la que las moléculas de gas escapan a través de una abertura muy pequeña en su contenedor se llama tasa de derrame. La tasa de derrame también depende de la frecuencia de colisiones con la pared. (Ver problema 4.12.) Otras propiedades del gas no dependen de la velocidad de colisión con la pared, sino de la velocidad con la que las moléculas de gas chocan entre sí. Pasamos ahora a algunas de estas propiedades. Para estas consideraciones, necesitamos describir el movimiento de una molécula con respecto a otra. Necesitamos la función de densidad de probabilidad para la velocidad relativa de dos partículas.

Para describir la velocidad relativa de dos partículas, se introducen coordenadas de velocidad relativa. Comencemos considerando un marco de coordenadas cartesianas, con\(x\) ejes\(y\) -, -, y z, cuyo origen está en un punto\(O\); utilizaremos\(Oxyz\) para designar este conjunto de ejes. Especificamos la ubicación de la partícula\(1\) por el vector\({\mathop{r}\limits^{\rightharpoonup}}_1=\left(x_1,y_1,z_1\right)=x_1\mathop{i}\limits^{\rightharpoonup}+y_1\mathop{j}\limits^{\rightharpoonup}+z_1\mathop{k}\limits^{\rightharpoonup}\) y la de partícula\(2\) por\({\mathop{r}\limits^{\rightharpoonup}}_2=\left(x_2,y_2,z_2\right)\). Dejamos que la ubicación del centro de masa de esta dos partículas

sistema ser especificado por\({\mathop{r}\limits^{\rightharpoonup}}_0=\left(x_0,y_0,z_0\right)\). El vector de partícula\(1\) a partícula\(2\),\({\mathop{r}\limits^{\rightharpoonup}}_{12}=\left(x_{12},y_{12},z_{12}\right)\), es la diferencia de vector

\[{\mathop{r}\limits^{\rightharpoonup}}_{12}={\mathop{r}\limits^{\rightharpoonup}}_2-{\mathop{r}\limits^{\rightharpoonup}}_1=\left(x_2-x_1,y_2-y_1,z_2-z_1\right)\nonumber \]

Cuando las partículas se mueven, estos vectores y sus componentes son funciones del tiempo. Usando la notación\({\dot{x}}_1={dx_1}/{dt}\), podemos especificar la velocidad de partícula\(1\), por ejemplo, como\({\mathop{v}\limits^{\rightharpoonup}}_1={d{\mathop{r}\limits^{\rightharpoonup}}_1}/{dt}=\left({\dot{x}}_1,{\dot{y}}_1,{\dot{z}}_1\right)\). Nuestro objetivo es encontrar el vector de velocidad relativa,\({\mathop{v}\limits^{\rightharpoonup}}_{12}={d{\mathop{r}\limits^{\rightharpoonup}}_{12}}/{dt}\). Llamamos a los componentes de\({\mathop{v}\limits^{\rightharpoonup}}_{12}\) las coordenadas de velocidad relativa.

Figura 7. El marco del centro de masa

La idea esencial subyacente a las coordenadas de velocidad relativa es que los vectores\({\mathop{r}\limits^{\rightharpoonup}}_0\) y\({\mathop{r}\limits^{\rightharpoonup}}_{12}\) contienen la misma información que los vectores\({\mathop{r}\limits^{\rightharpoonup}}_1\) y\({\mathop{r}\limits^{\rightharpoonup}}_2\). Esto equivale a decir que podemos transformar las ubicaciones según lo especificado por\(\left(x_1,y_1,z_1\right)\) y\(\left(x_2,y_2,z_2\right)\) a las mismas ubicaciones especificadas por\(\left(x_0,y_0,z_0\right)\) y\(\left(x_{12},y_{12},z_{12}\right)\), y viceversa. Para lograr esto, escribimos la ecuación que define el\(x\) componente -del centro de masa,\(x_0\):

\[m_1\left(x_1-x_0\right)+m_2\left(x_2-x_0\right)=0\nonumber \]

a la que reorganizamos

\[\frac{x_1}{m_2}+\frac{x_2}{m_1}=\left(\frac{1}{m_1}+\frac{1}{m_2}\right)x_0\nonumber \]

Las relaciones correspondientes se pueden escribir para los componentes\(y\) - y\(z\) -componentes. Resulta útil introducir la masa reducida,\(\mu\), definida por

\[\frac{1}\mu=\frac{1}{m_1}+\frac{1}{m_2}\nonumber \]

Usando la masa reducida, podemos expresar las coordenadas del centro de masa en términos de las coordenadas de las partículas individuales. Es decir,

\[x_0=\left(\frac\mu{m_2}\right)x_1+\left(\frac\mu{m_1}\right)x_2\nonumber \]

\[y_0=\left(\frac\mu{m_2}\right)y_1+\left(\frac\mu{m_1}\right)y_2\nonumber \]

\[z_0=\left(\frac\mu{m_2}\right)z_1+\left(\frac\mu{m_1}\right)z_2\nonumber \]

Ya que, por definición, también tenemos

\[x_{12}=x_2-x_1\nonumber \]\[y_{12}=y_2-y_1\nonumber \]\[z_{12}=z_2-z_1\nonumber \]

hemos desarrollado la transformación desde\(\left(x_0,y_0,z_0\right)\) y\(\left(x_{12},y_{12},z_{12}\right)\) hacia\(\left(x_1,y_1,z_1\right)\) y\(\left(x_2,y_2,z_2\right)\). Se encuentra fácilmente que la transformación inversa es

\[x_1=x_0-\left(\mu/{m_1}\right)x_{12}\nonumber \]

\[y_1=y_0-\left(\mu/{m_1}\right)y_{12}\nonumber \]

\[z_1=z_0-\left(\mu/{m_1}\right)z_{12}\nonumber \]

\[x_2=x_0+\left(\mu/{m_2}\right)x_{12}\nonumber \]

\[y_2=y_0+\left(\mu/{m_2}\right)y_{12}\nonumber \]

\[z_2=z_0+\left(\mu/{m_2}\right)z_{12}\nonumber \]

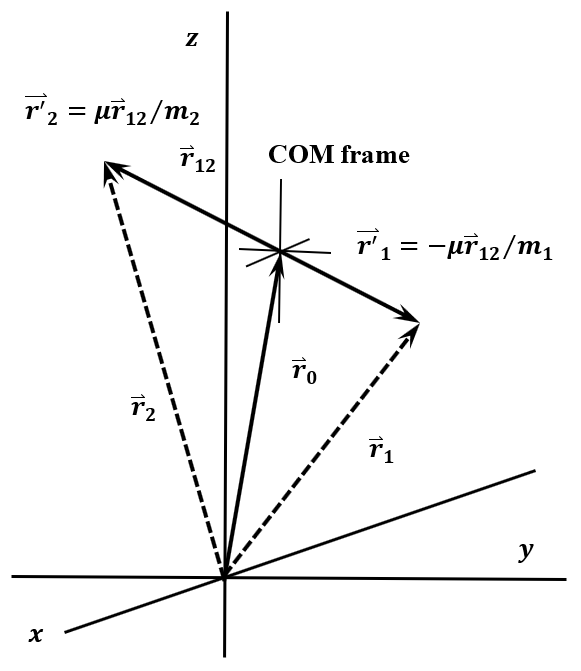
Ahora podemos crear dos nuevos marcos de coordenadas cartesianas. Cuál de estos es más útil depende del objetivo del análisis particular que tengamos a la mano. Llamamos al primero el marco de centro de masa,\(O_Ox^{'}y^{'}z^{'}\). Se esboza en la Figura 7. Los\(z{'}\) ejes\(x{'}\)\(y{'}\) -, -, y -de\(O_Ox^{'}y^{'}z^{'}\) son paralelos a los ejes correspondientes de\(Oxyz\), pero su origen,\(O_O\), está siempre en el punto ocupado por el centro de masa del sistema de dos partículas. En este marco de referencia, las coordenadas de las partículas\(1\) y\(2\) son sus desplazamientos desde el centro de masa:

\[x^{'}_1=x_1-x_0=-\left(\mu/{m_1}\right)x_{12}\nonumber \]

\[y^{'}_1=y_1-y_0=-\left(\mu/{m_1}\right)y_{12}\nonumber \]

\[z^{'}_1=z_1-z_0=-\left(\mu/{m_1}\right)z_{12}\nonumber \]

\[x^{'}_2=x_2-x_0=\left(\mu/{m_2}\right)x_{12}\nonumber \]

\[y^{'}_2=y_2-y_0=\left(\mu/{m_2}\right)y_{12}\nonumber \]

\[z^{'}_2=z_2-z_0=\left(\mu/{m_2}\right)z_{12}\nonumber \]

El marco del centro de masa es particularmente útil para analizar las interacciones entre partículas colisionantes.

Figura 8. El marco centrado en partícula-uno.

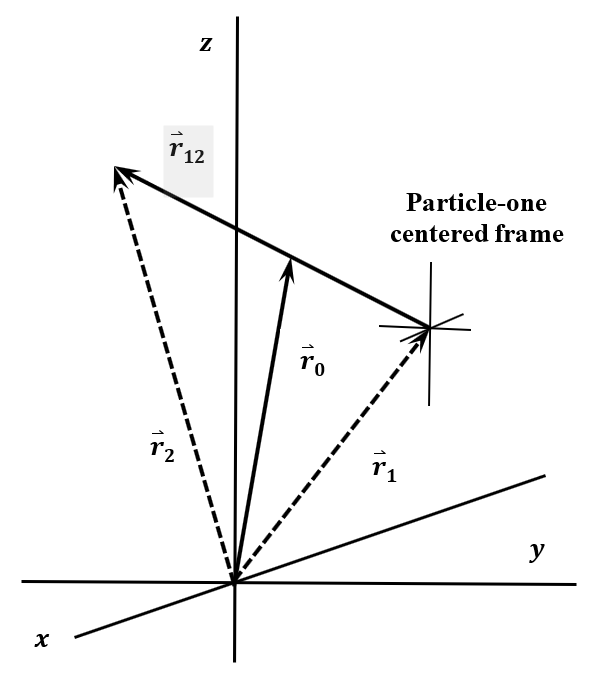
Para nuestros propósitos, es más útil un tercer marco de coordenadas cartesianas, que denotaremos el\(O_1x^{''}y^{''}z^{''}\) marco. Se esboza en la Figura 8. Los\(z^{''}\) ejes\(x^{''}\) -,\(y^{''}\) -, y -de\(O_1x^{''}y^{''}z^{''}\) son paralelos a los ejes correspondientes de\(Oxyz\), pero su origen,\(O_1\), está siempre en el punto ocupado por la partícula 1. En este marco de referencia, las coordenadas de las partículas 1 y 2 son

\[x^{''}_1=0\nonumber \]

\[y^{''}_1=0\nonumber \]

\[z^{''}_1=0\nonumber \]

\[x^{''}_2=x_2-x_1=x_{12}\nonumber \]

\[y^{''}_2=y_2-y_1=y_{12}\nonumber \]

\[z^{''}_2=z_2-z_1=z_{12}\nonumber \]

y las coordenadas del centro de masa son

\[x^{''}_0=x_0-x_1={\mu x_{12}}/{m_1}\nonumber \]

\[y^{''}_0=y_0-y_1={\mu y_{12}}/{m_1}\nonumber \]

\[z^{''}_0=z_0-z_1={\mu z_{12}}/{m_1}\nonumber \]

El\(O_1x^{''}y^{''}z^{''}\) marco a veces también se llama marco de centro de masa. Para evitar confusiones, llamamos\(O_1x^{''}y^{''}z^{''}\) al marco centrado en partícula-uno. En el marco centrado en la partícula una, la partícula\(1\) es estacionaria en el origen. Con su cola en el origen, el vector\({\mathop{r}\limits^{\rightharpoonup}}_{12}=\left(x_{12},y_{12},z_{12}\right)\) especifica la posición de la partícula\(2\).

Nos interesa la velocidad relativa de las partículas\(1\) y\(2\). Los componentes de velocidad para las partículas\(1\) y\(2\), y para su velocidad relativa, se obtienen al encontrar los derivados del tiempo de los componentes de desplazamiento correspondientes. Dado que las transformaciones de las coordenadas de desplazamiento son lineales, los componentes de velocidad se transforman de un marco de referencia a otro exactamente de la misma manera que lo hacen los componentes de desplazamiento. Tenemos

\[{\mathop{v}\limits^{\rightharpoonup}}_0={d{\mathop{r}\limits^{\rightharpoonup}}_0}/{dt}=\left({\dot{x}}_0,{\dot{y}}_0,{\dot{z}}_0\right)\nonumber \]

y

\[{\mathop{v}\limits^{\rightharpoonup}}_{12}={d{\mathop{r}\limits^{\rightharpoonup}}_{12}}/{dt}=\left({\dot{x}}_{12},{\dot{y}}_{12},{\dot{z}}_{12}\right)\nonumber \]

El vector\({\mathop{v}\limits^{\rightharpoonup}}_{12}\) especifica la velocidad de la partícula\(2\), relativa a una partícula estacionaria\(1\). Así como\({\mathop{r}\limits^{\rightharpoonup}}_0\) y\({\mathop{r}\limits^{\rightharpoonup}}_{12}\) contienen la misma información que los vectores\({\mathop{r}\limits^{\rightharpoonup}}_1\) y\({\mathop{r}\limits^{\rightharpoonup}}_2\), los vectores\({\mathop{v}\limits^{\rightharpoonup}}_0\) y\({\mathop{v}\limits^{\rightharpoonup}}_{12}\) contienen la misma información que\({\mathop{v}\limits^{\rightharpoonup}}_1\) y\({\mathop{v}\limits^{\rightharpoonup}}_2\). Dado que un desplazamiento paralelo deja un vector sin cambios, cada uno de estos vectores es el mismo en cualquiera de los tres marcos de referencia. En § 11, encontramos la función de densidad de probabilidad para la magnitud de la velocidad relativa escalar,\(v_{12}=\left|{\mathop{v}\limits^{\rightharpoonup}}_{12}\right|\). Dado que la probabilidad es independiente de la dirección, la probabilidad de que dos moléculas tengan velocidad relativa\({\mathop{v}\limits^{\rightharpoonup}}_{12}\) es la misma que la que tienen velocidad relativa\({-\mathop{v}\limits^{\rightharpoonup}}_{12}\). (En coordenadas esféricas, si\({\mathop{v}\limits^{\rightharpoonup}}_{12}=\left(v_{12},\theta ,\varphi \right)\), entonces\(-{\mathop{v}\limits^{\rightharpoonup}}_{12}=\left(v_{12},\theta +\pi ,\varphi +\pi \right)\).) La probabilidad y magnitud de la velocidad relativa son independientes de qué partícula, si la otra, elegimos ver como estacionarias; son independientes de si las partículas se acercan o retroceden entre sí.