26.3: Esfuerzo cortante y deformación

La superficie del material también puede estar sometida a fuerzas tangenciales que producen una acción de cizallamiento. Considera un bloque de altura h y área A, en el que\(\overrightarrow{\mathbf{F}}_{\mathrm{tan}}\) se aplica una fuerza tangencial a la superficie superior. La superficie inferior se mantiene fija. La superficie superior cortará un ángulo\(\alpha\) correspondiente a un desplazamiento horizontal\(\delta x\) La geometría de la acción de cizallamiento se muestra en la Figura 26.5.

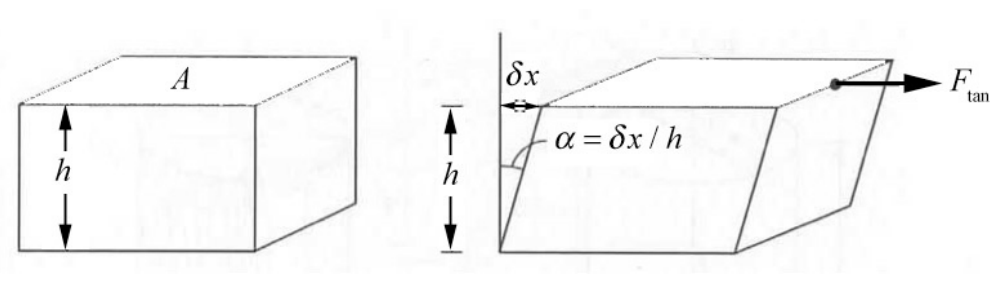
Figura 26.5: Fuerzas de corte

El esfuerzo cortante se define como la relación entre la fuerza tangencial y el área de la sección transversal de la superficie sobre la que actúa,

\ begin {ecuación}\ sigma_ {S} =\ frac {F_ {\ tan}} {A}\ fin {ecuación}

La deformación por cizallamiento se define como la relación entre el desplazamiento horizontal y la altura del bloque,

\ begin {ecuación}\ alpha=\ frac {\ delta x} {h}\ end {ecuación}

Para muchos materiales, cuando el esfuerzo cortante es suficientemente pequeño, el experimento muestra que una relación de la Ley de Hooke se mantiene en que el esfuerzo cortante es proporcional a la deformación por cizallamiento,

\ begin {ecuación}\ frac {F_ {\ text {tan}}} {A} =S\ frac {\ delta x} {h}\ quad\ text {(Ley de Hooke)}\ end {ecuación}

donde la constante de proporcional,\(S\), se llama el módulo de cizallamiento. Cuando el ángulo de deformación es pequeño\(\delta x / h=\tan \alpha \simeq \sin \alpha \simeq \alpha\), y la ecuación (26.3.3) se convierte en

\ begin {ecuación}\ frac {F_ {\ text {tan}}} {A}\ simeq\(S\)\ alpha\ quad\ text {(Ley de Hooke)}\ end {ecuación}

En el Cuadro 26.2 se tabula el módulo de cizallamiento para diversos materiales.

Cuadro 26.2: Módulo de cizallamiento para diversos materiales

\ begin {ecuación}\ begin {array} {|l|l|}
\ hline\ text {Material} &\ text {Módulo de cizallamiento,}\(S\)\ text {(Pa)}
\\\ hline\ text {Níquel} & 7.8\ veces 10^ {10}
\\ hline\ texto {Hierro} & 7.7\ veces 10^ {10}\
\ hline\ texto {Acero} & 7.5\ times 10^ {10}\
\ hline\ text {Cobre} & 4.4\ veces 10^ {10}\
\ hline\ texto {Latón} & 3.5\ veces 10^ {10}\
\ hline\ texto {Aluminio} & 2.5\ veces 10^ {10}\\ hline
\ texto {Cristal de Corona} & 2.5\ veces 10^ {10}\\
\ hline\ text {Lead} & 0.6\ times 10^ {10}\
\ hline\ text {Rubber} & 2\ times 10^ {5} -10\ times 10^ {5}\
\ hline
\ end {array}\ end {ecuación}

Ejemplo 26.1: Alambre estirado

Un objeto de masa\(1.5 \times 10^{1} \mathrm{kg}\) está colgando de un extremo de un alambre de acero. El alambre sin la masa tiene una longitud no estirada de 0.50 m. ¿Cuál es la deformación y elongación resultantes del alambre? El área de la sección transversal del cable es\(1.4 \times 10^{-2} \mathrm{cm}^{2}\).

Solución: Cuando el objeto colgante está unido al cable, la fuerza al final del cable que actúa sobre el objeto equilibra exactamente la fuerza gravitacional. Por lo tanto, según la Tercera Ley de Newton, la fuerza de tracción que tensa el alambre es

\ begin {ecuación} F_ {\ perp} =m g\ end {ecuación}

Podemos calcular la tensión en el alambre a partir de la Ley de Hooke (Ecuación (26.2.3)) y el valor del módulo de Young para el acero\(20 \times 10^{10} \mathrm{Pa} \text { (Table } \left.26.1\right)\).

\ begin {ecuación}\ frac {\ delta l} {l_ {0}} =\ frac {F_ {\ perp}} {Y A} =\ frac {m g} {Y A} =\ frac {\ izquierda (1.5\ veces 10^ {1}\ mathrm {kg}\ derecha)\ izquierda (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ derecha)} {\ izquierda (2.0\ veces 10^ {11}\ mathrm {Pa}\ derecha)\ izquierda (1.4\ veces 10^ {-6}\ mathrm {m} ^ {2}\ derecha)} =5.3\ veces 10^ {-4}\ final {ecuación}

El alargamiento\(\delta l\) del alambre es entonces

\ begin {ecuación}\ delta l=\ frac {m g} {Y A} l_ {0} =\ left (5.3\ times 10^ {-4}\ right) (0.50\ mathrm {m}) =2.6\ times 10^ {-4}\ mathrm {m}\ end {ecuación}