4.6: Movimiento sin fuerza de una parte superior rígida asimétrica

Por “top asimétrico” me refiero a un cuerpo cuyos tres momentos principales de inercia son desiguales. Si bien a menudo pensamos en un “top” como un cuerpo simétrico que gira sobre una mesa, en esta sección el “top” no necesariamente será simétrico, y no estará en contacto con ninguna mesa, ni de hecho sometido a fuerzas externas o pares.

Una descripción completa del movimiento de un top asimétrico es bastante complicada, y por lo tanto todo lo que intentaremos en este capítulo es una descripción cualitativa de ciertos aspectos del movimiento. Que nuestra descripción vaya a ser “cualitativa” no implica de ninguna manera que esta sección no vaya a estar repleta de ecuaciones o que podamos darle un descanso a nuestros pobres cerebros.

El primer punto que podemos hacer es que, siempre que no actúen pares externos sobre el cuerpo, su momento angular\(\bf L \) es constante en magnitud y dirección. Un segundo punto es que, siempre que el cuerpo sea rígido y no tenga grados internos de libertad, la energía cinética rotacional\(T\) es constante. Me ocupo brevemente de los cuerpos no rígidos en la Sección 4.7. Aunque el vector de velocidad angular no\( \boldsymbol\omega \) se fija en ninguna magnitud y dirección, y el cuerpo puede voltear una y otra vez, estas dos condiciones imponen algunas restricciones de la magnitud y dirección de\( \boldsymbol\omega \).

Vamos a examinar estas dos condiciones para ver qué limitaciones se imponen\( \boldsymbol\omega \). Una de las cosas que encontraremos es que la rotación de un cuerpo alrededor de un eje principal de mayor o menor momento de inercia es estable frente a pequeños desplazamientos, mientras que la rotación alrededor del eje principal del momento intermedio de inercia es inestable.

La ausencia de un par externo significa que el momento angular es constante:

\[ L^{2} = L^{2}_{1} + L^{2}_{2} + L^{2}_{3} = constant, \tag{4.6.1}\label{eq:4.6.1} \]

para que, en todo momento,

\[ I^{2}_{1}\omega_{1}^{2}+I^{2}_{2}\omega_{2}^{2}+I^{2}_{3}\omega_{3}^{2} = L^{2} \tag{4.6.2}\label{eq:4.6.2} \]

Así, para un dado\( L\). los componentes de velocidad angular siempre satisfacen

\[ \frac{\omega^{2}_{1}}{(L/I_{1})^{2}} + \frac{\omega^{2}_{2}}{(L/I_{2})^{2}} + \frac{\omega^{2}_{3}}{(L/I_{3})^{2}}= 1. \tag{4.6.3}\label{eq:4.6.3} \]

Es decir, el vector de velocidad angular está restringido de tal manera que la punta del vector\( \boldsymbol\omega\) está siempre en la superficie de un elipsoide de semiejes\( \frac{L}{I_{1}}\),\( \frac{L}{I_{2}}\),\( \frac{L}{I_{3}}\),

Además de la constancia del momento angular, la energía cinética también es constante:

\[ \frac{1}{2}I_{1}\omega_{1}^{2} + \frac{1}{2}I_{2}\omega_{2}^{2} + \frac{1}{2}I_{3}\omega_{3}^{2}= T \tag{4.6.4}\label{eq:4.6.4} \]

Así, la punta del vector de velocidad angular también debe estar en la superficie del elipsoide

\[ \frac{\omega^{2}_{1}}{(\sqrt{2T/I_{1}})^{2}}+\frac{\omega^{2}_{2}}{(\sqrt{2T/I_{2}})^{2}} +\frac{\omega^{2}_{3}}{(\sqrt{2T/I_{3}})^{2}} = 1. \tag{4.6.5}\label{eq:4.6.5} \]

Este elipsoide (que es similar en forma al elipsoide momental) tiene semiejes\( \sqrt{2T/I_{1}}, \sqrt{2T/I_{2}}, \sqrt{2T/I_{3}}. \)

Así, la forma en que el cuerpo cae una y otra vez,\( \boldsymbol\omega \) se restringe en magnitud y dirección para que su punta esté en la curva donde se cruzan estas dos elipses.

Ejemplo\(\PageIndex{1}\)

Supongamos, que tenemos un cuerpo rígido con

• \( I_{1}\)= 0.2 kgm ²
• \( I_{2}\)= 0.3 kgm ²
• \( I_{3}\)= 0.5 kgm ²

y que lo pusimos en movimiento de tal manera que el momento angular y la energía cinética sean L = 4 J s y T = 20 J.

(El momento angular y la energía cinética estarán determinados por la magnitud y dirección del vector de velocidad inicial por el cual se pone en movimiento).

La punta de\( \boldsymbol\omega \) está restringida para estar en la curva de intersección de los dos elipsoides

\[ \frac{\omega_{1}^{2}}{20^{2}}+\frac{\omega_{2}^{2}}{13.3^{2}}+ \frac{\omega_{3}^{2}}{8^{2}} = 1 \tag{4.6.6}\label{eq:4.6.6} \]

y

\[ \frac{\omega_{1}^{2}}{14.14^{2}}+\frac{\omega_{2}^{2}}{11.55^{2}}+ \frac{\omega_{3}^{2}}{8.94^{2}} = 1 \tag{4.6.7}\label{eq:4.6.7} \]

No es fácil (o no lo encuentro así) imaginar cómo se ve esta curva de intersección en el espacio tridimensional, pero uno de mis alumnos, Leif Petersen, preparó el dibujo a continuación, y le agradezco el permiso para reproducirlo aquí. Se puede ver que la curva de intersección no es una curva plana.

En caso de que sea de alguna ayuda, es posible que desee señalar que las ecuaciones\( \ref{eq:4.6.6}\) y se\( \ref{eq:4.6.7}\) pueden escribir

\[ 4 \omega^{2}_{1} + 9 \omega^{2}_{2} + 25 \omega^{2}_{3} = 1600 \tag{4.6.8}\label{eq:4.6.8} \]

y

\[ 2 \omega^{2}_{1} + 3 \omega^{2}_{2} + 5 \omega^{2}_{3} = 400 \tag{4.6.9}\label{eq:4.6.9} \]

pero voy a dejar las ecuaciones en la forma\( \ref{eq:4.6.6}\) y\( \ref{eq:4.6.7}\), y en la figura IV.7, voy a esbozar un octante de las dos superficies elipsoidales.

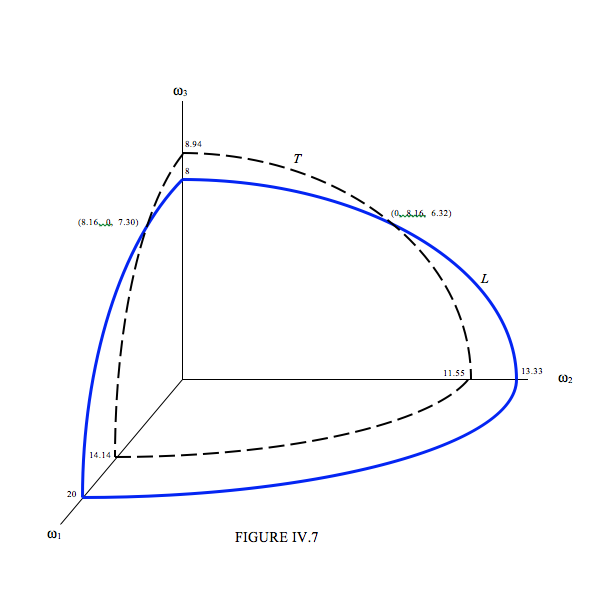
La curva azul continua muestra un octante del elipsoide\( L\) = constante, y la curva negra discontinua muestra un octante del elipsoide\( T\) = constante. El vector de momento angular puede terminar solo en la curva (no dibujada) donde se cruzan los dos elipsoides. En la Figura IV.7 se indican dos puntos en la curva. Si, por ejemplo,\( \boldsymbol\omega \) se orienta de manera que\( \omega_{1} \) = 0, los otros dos componentes deben ser\( \omega_{2} \) = 8.16 y\( \omega_{3} \) = 6.32. Si está orientado de manera que\( \omega_{3} \) = 0, los otros dos componentes deben ser\( \omega_{3} \) = 7.30 y\( \omega_{1} \) = 8.16. Si\( \omega_{3} \) = 0, no hay soluciones reales para\( \omega_{1} \) y\( \omega_{2} \). Esto significa que, para los valores dados de\( L\) y\( T\),\( \omega_{3} \) no puede ser cero.

Ahora voy a dirigirme a la estabilidad de rotación cuando inicialmente se establece una parte superior simétrica para girar alrededor de uno de sus ejes principales, que tomaré como el\( z\) eje -eje. Supondremos que inicialmente\( \omega_{1} \) =\( \omega_{2} \) = 0, y\( \omega_{3} \) =\( \Omega\). En ese caso el momento angular y la energía cinética son\( L = I_{3}\Omega \) En cualquier movimiento posterior, la punta de\( T = I_{3}\Omega^{2} \) se restringe a moverse a lo largo de la curva de intersección de los elipsoides dada por las ecuaciones\( \ref{eq:4.6.3}\) y\( \ref{eq:4.6.5}\). Es decir, a lo largo de la curva de intersección de los elipsoides

\ [\ frac {\ omega_ {1} ^ {2}} {(\ frac {I_ {3}} {I_ {1}}\ Omega) ^2} +\ frac {\ omega_ {2} ^ {2}} {(\ frac {I_ {3}} {I_ {2}}\ Omega) ^2} +
\ frac {\ omega_ {3} ^ {2}} {\ Omega^ {2}} = 1\ tag {4.6.10}\ etiqueta {eq:4.6.10}\]

y

\ [\ frac {\ omega_ {1} ^ {2}} {(\ sqrt {\ frac {I_ {3}} {I_ {1}}\ Omega) ^2} +\ frac {\ omega_ {2} ^ {2}} {(\ sqrt {\ frac {I_ {3}} {I_ {2}}\ Omega) ^2} +
\ frac {\ omega_ {3} ^ {2}} {\ Omega^ {2}} = 1\ tag {4.6.11}\ etiqueta {eq:4.6.11}\]

Para un ejemplo específico, supongo que los momentos de inercia están en la proporción\( 2:3:5\), y consideraremos tres casos a su vez.

Caso I. Rotación alrededor del eje de menor momento de inercia. Es decir, vamos a tomar\( I_{3}=2\), \( I_{1}=3\), \( I_{2}=5\). Since \( I_{3}\) is the smallest moment of inertia, each of the ratios \( \frac{I_{3}}{I_{1}}\) and \( \frac{I_{3}}{I_{2}}\) are less than 1, and \( \sqrt{\frac{I_{3}}{I_{1}}} > \frac{I_{3}}{I_{1}} \quad and \sqrt{\frac{I_{3}}{I_{2}}} > \frac{I_{3}}{I_{2}} \) The two ellipsoids are

\[ \frac{\omega^{2}_{1}}{(0.667 \Omega)^2} + \frac{\omega^{2}_{2}}{(0.400 \Omega)^2} + \frac{\omega^{2}_{3}}{\Omega^{2}} = 1 \tag{4.6.12}\label{eq:4.6.12} \]

y

\[ \frac{\omega^{2}_{1}}{(0.816\Omega)^2} + \frac{\omega^{2}_{2}}{(0.632 \Omega)^2} + \frac{\omega^{2}_{3}}{\Omega^{2}} = 1 \tag{4.6.13}\label{eq:4.6.13} \]

Voy a tratar de bosquejar estos:

Inicialmente, suponemos, el cuerpo se puso en movimiento girando alrededor del\( z\) eje -con velocidad angular\( \Omega \), lo que determina los valores de\( L\) y\( T\), que permanecerán constantes. La punta del vector\( \omega \) está restringida a permanecer en la superficie del elipsoide\( L\) = 0 y en el elipsoide\( T\) = 0, y por lo tanto en la intersección de estas dos superficies. Pero estas dos superficies tocan sólo en un punto, a saber (\( \omega_{1}, \omega_{2}, \omega_{3} \)) = (0, 0,\( \Omega \)). Así ahí el vector\( \omega \) permanece, y la rotación es estable.

Caso II. Rotación alrededor del eje de mayor momento de inercia. Es decir, vamos a tomar\( I_{3}=5\),\( I_{1}=2\),\( I_{2}=3\). Dado que\( I_{3}\) es el mayor momento de inercia, cada una de las proporciones\( \frac{I_{3}}{I_{1}}\) y\( \frac{I_{3}}{I_{2}}\) son mayores que 1, y\( \sqrt{\frac{I_{3}}{I_{1}}} < \frac{I_{3}}{I_{1}}\) y\( \sqrt{\frac{I_{3}}{I_{2}}} < \frac{I_{3}}{I_{2}}\) Los dos elipsoides son

\[ \frac{\omega_{1}^{2}}{(2.50\Omega)^{2}} + \frac{\omega_{2}^{2}}{(1.67\Omega)^{2}} + \frac{\omega_{3}^{2}}{\Omega^{2}}=1 \tag{4.6.14}\label{eq:4.6.14} \]

y

\[ \frac{\omega_{1}^{2}}{(1.58\Omega)^{2}} + \frac{\omega_{2}^{2}}{(1.29\Omega)^{2}} + \frac{\omega_{3}^{2}}{\Omega^{2}}=1 \tag{4.6.15}\label{eq:4.6.15} \]

Voy a tratar de bosquejar estos:

Nuevamente, y por la misma razón que para el Caso I, vemos que esta moción es estable.

Caso III. Rotación alrededor del eje intermedio. Es decir, vamos a tomar\( I_{3}=3\), \( I_{1}=5\), \( I_{2}=2\). This time \( \frac{I_{3}}{I_{1}}\) is less than 1 and \( \frac{I_{3}}{I_{2}}\) is less than 1, y\( \sqrt{\frac{I_{3}}{I_{1}}} < \frac{I_{3}}{I_{1}}\) y\( \sqrt{\frac{I_{3}}{I_{2}}} < \frac{I_{3}}{I_{2}} \) Los dos elipsoides son

\[ \frac{\omega^{2}_{1}}{(0.60 \Omega)} + \frac{\omega^{2}_{2}}{(1.50 \Omega)^2} + \frac{\omega^{2}_{3}}{\Omega^{2}} = 1 \tag{4.6.16}\label{eq:4.6.16} \]

y

\[ \frac{\omega^{2}_{1}}{(0.77\Omega)^2} + \frac{\omega^{2}_{2}}{(1.22 \Omega)^2} + \frac{\omega^{2}_{3}}{\Omega^{2}} = 1 \tag{4.6.17}\label{eq:4.6.17} \]

Voy a tratar de bosquejar estos:

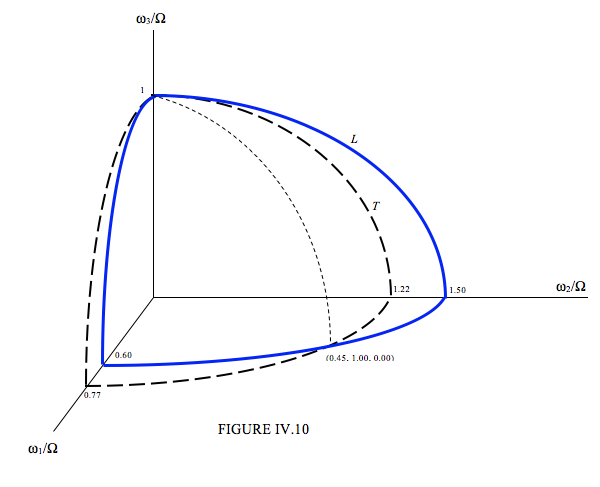
A diferencia de la situación para los Casos I y II, en los que los dos elipsoides tocan en un solo punto, las dos elipses para el Caso III se cruzan en la curva que se muestra como una línea punteada en la figura IV.10. Por lo tanto, no\( \omega\) se restringe a mentir a lo largo del\( z\) eje, sino que puede moverse a cualquier parte a lo largo de la línea La moción, por lo tanto, no es estable.

Debes experimentar lanzando un cuerpo al aire de tal manera que lo dejes girar alrededor de uno de sus ejes principales. Un bloque rectangular servirá, aunque el efecto es particularmente notable con algo así como una bate de tenis de mesa.

Aquí hay otro enfoque para alcanzar el mismo resultado. Imaginamos una peonza asimétrica girando alrededor de uno de sus ejes principales con velocidad angular\ (\ negrita\ omega\ =\ omega\ hat {\ bf z}). Entonces se le da una pequeña perturbación, de manera que su velocidad angular es ahora.

\[ \omega = \epsilon \hat{ \bf x} + \eta\hat{\bf y} + \omega_{z}\hat{ \bf z} \tag{4.6.18}\label{eq:4.6.18} \]

Aquí las cantidades “sombreadas” son los vectores ortogonales unitarios;\( \epsilon \) y\( \eta \) se supone que son pequeñas comparadas con\( \omega_{z} \). Las ecuaciones de Euler son:

\[ I_{1} \dot{\epsilon} = \eta \omega_{Z} (I_{2} - I_{3}), \tag{4.6.19}\label{eq:4.6.19} \]

\[ I_{1} \dot{\eta} = \omega_{Z} \epsilon (I_{3} - I_{1}), \tag{4.6.20}\label{eq:4.6.20} \]

\[ I_{1} \dot{\omega_{Z}} = \epsilon \eta (I_{1} - I_{2}). \tag{4.6.21}\label{eq:4.6.21} \]

Si\( \epsilon \eta << \dot{\omega_{Z}} , \) entonces\( \omega_{Z}\) es aproximadamente constante. Eliminación\( \eta \) de los rendimientos de las dos primeras ecuaciones

\[ \ddot{\epsilon} = - [\frac{(I_{2} - I_{3})(I_{1}-I_{3})\omega_{z}^{2}}{I_{1}I_{2}}]\epsilon \tag{4.6.22}\label{eq:4.6.22} \]

La eliminación de\( \epsilon \) en su lugar da como resultado una ecuación similar en\( \eta \).

Si\( I_{3}\) es el mayor o el menor de los tres momentos de inercia, los dos paréntesis en el denominador tienen el mismo signo, por lo que la expresión entre paréntesis es positiva. La ecuación\( \ref{eq:4.6.22}\) es entonces la ecuación para el movimiento armónico simple, y el movimiento es estable. Si, sin embargo,\( I_{3}\) es intermedio entre los otros dos, los dos paréntesis tienen signo opuesto, y la expresión entre paréntesis en negativo. En ese caso\( \epsilon\) y\( \eta\) aumentar exponencialmente, y el movimiento es inestable.

El señor Neil Honkanen de la Universidad de Victoria realizó un experimento para ilustrar la estabilidad de la rotación sobre los tres ejes principales. El cuerpo en cuestión era un pequeño “ladrillo” de acero dulce (densidad 7.83 g/cm ³) de dimensiones 3/8 pulgada × 3/4 pulgada × 1 1/2 pulgada, masa 54.1 g En figuras redondas, esto corresponde a momentos principales de inercia\( A_{0}\) = 2 ×10 ^{- 6} kg m ², \( B_{0}\)= 7 × 10 ^{- 6} kg m ²,\( C_{0}\) = 8 × 10 ^{- 6} kg m ². Lo suspendió de un electroimán, que puso en rotación a unas 25 revoluciones por segundo, para luego dejarlo caer, mientras lo fotografiaba estroboscopicamente. Realizó tres experimentos de rotación respectivamente sobre los tres ejes principales. Se puede ver en las fotografías de abajo que la rotación es estable cuando la rotación es alrededor de los ejes de mayor o menor momento de inercia, pero es inestable cuando la rotación es alrededor del eje de momento intermedio de inercia.