4.5: Ecuaciones de movimiento de Euler

En nuestra primera introducción a la mecánica clásica, aprendemos que cuando un par externo actúa sobre un cuerpo, su momento angular cambia (y si ningún par externo actúa sobre un cuerpo, su momento angular no cambia). Aprendemos que la tasa de cambio del momento angular es igual al par aplicado. En los primeros ejemplos simples que solemos encontrar, un cuerpo simétrico gira alrededor de un eje de simetría, y el par también se aplica alrededor de este mismo eje. El momento angular es justo\( I\omega\), y así la afirmación de que el par es igual a la tasa de cambio del momento angular es meramente\( \tau = I \dot{\omega}\) y eso es todo lo que hay que hacer.

Posteriormente, aprendemos que\( \bf{L}\) =\( I \boldsymbol\omega\), donde\( \bf{l}\) es un tensor, y\( \bf{L}\) y no\( \boldsymbol\omega\) son paralelos. Hay tres momentos principales de inercia, y\( \bf{L}\),\( \boldsymbol\omega\) y el par aplicado tiene\( \boldsymbol\tau \) cada uno tres componentes, y la declaración “torque es igual a la tasa de cambio del momento angular” de alguna manera se vuelve mucho menos fácil.

Las ecuaciones de Euler solucionan esto, y nos dan una relación entre los componentes de la\( \boldsymbol\tau \),\( \bf{l}\) y\( \boldsymbol\omega\).

Para la Figura IV.5, acabo de reproducir, con algunas pequeñas modificaciones, la Figura III.19 de mis notas en este sitio Web sobre Mecánica Celestial, donde definí ángulos eulerianos. Nuevamente se sugiere que quienes no están familiarizados con los ángulos eulerianos consulten el Capítulo III de la Mecánica Celestial.

En la Figura IV.5,\( Oxyz\) se encuentran ejes fijos al espacio, y\( Ox_{0}y_{0}z_{0}\) son los ejes principales fijos al cuerpo. El eje\( Oy_{0}\) está detrás del plano de tu pantalla; tendrás que mirar dentro de tu monitor para encontrarlo.

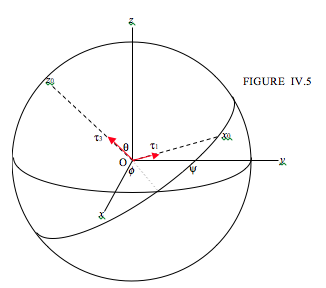
Supongo que un par externo\( \boldsymbol\tau \) actúa sobre el cuerpo, y he dibujado los componentes\( \tau_{1} \) y\( \tau_{3} \). Ahora supongamos que el cuerpo gira de tal manera que el ángulo euleriano\( \psi \) iba a aumentar por\( \delta\psi\). Creo que se acordará fácilmente que el trabajo realizado en el cuerpo es\( \tau_{3}\delta\psi\). Esto significa, siguiendo nuestra definición de fuerza generalizada en la Sección 4.4, que\( \tau_{3} \) es la fuerza generalizada asociada a la coordenada generalizada\( \psi\). Habiendo establecido eso, ahora podemos aplicar la Ecuación Lagrangiana 4.4.1:

\[ \ \frac{\text{d}}{\text{d}t} (\frac{\partial T}{\partial \dot{\psi}})-\frac{\partial T}{\partial \psi} = \tau_{3} \tag{4.5.1}\label{eq:4.5.1} \]

Aquí la energía cinética es la expresión que ya hemos establecido en la Ecuación 4.3.6. A pesar del aspecto un tanto temible de la Ecuación 4.3.6, es bastante fácil\( \ref{eq:4.5.1}\) aplicarle Ecuación. Así

\[ \ \frac{\partial T}{\partial \dot{\psi}}= I_{3}(\dot{\phi}cos\theta + \psi) = I_{3}\omega \tag{4.5.2}\label{eq:4.5.2} \]

donde he hecho uso de la Ecuación 4.2.3.

Por lo tanto

\[ \ \frac{\text{d}}{\text{d}t}(\frac{\partial T}{\partial \dot{\psi}}) = I_{3}\dot{\omega_{3}} \tag{4.5.3}\label{eq:4.5.3} \]

Y, si hacemos uso de las Ecuaciones 4.2.1,2,3, es fácil de obtener

\[ \ \frac{\partial T}{\partial \psi}) = I_{1}\omega_{1}\omega_{2}- I_{2}\omega_{2}\omega_{2} = \omega_{1}\omega_{2}(I_{1}-I_{2}) \tag{4.5.4}\label{eq:4.5.4} \]

Así Ecuación\( \ref{eq:4.5.1}\) se convierte en:

\[ \ I_{3}\dot{\omega_{3}} - (I_{1} -I_{2})\omega_{1}\omega_{1} = \tau_{3} \tag{4.5.5}\label{eq:4.5.5} \]

Esta es una de las Ecuaciones Eulerianas del movimiento.

Ahora bien, aunque vimos que esa\( \tau_{3}\) es la fuerza generalizada asociada a la coordenada y, quedaremos igualmente claros que no\( \tau_{1}\) es la fuerza generalizada asociada con q, ni\( \tau_{2}\) la fuerza generalizada asociada a\( \phi \). Sin embargo, no tenemos que pensar en cuáles son las fuerzas generalizadas asociadas a estas dos coordenadas; es mucho más fácil que eso. Para obtener las dos Ecuaciones Eulerianas restantes, todo lo que se necesita es llevar a cabo una permutación cíclica de los subíndices en la Ecuación\( \ref{eq:4.5.5}\). Así, las tres Ecuaciones Eulerianas son:

\[ \ I_{1}\dot{\omega_{1}} - (I_{2}-I_{2})\omega_{2}\omega_{3} = \tau_{1} , \tag{4.5.6}\label{eq:4.5.6} \]

\[ \ I_{2}\dot{\omega_{2}} - (I_{3}-I_{1})\omega_{3}\omega_{1} = \tau_{2} , \tag{4.5.7}\label{eq:4.5.7} \]

\[ \ I_{3}\dot{\omega_{3}} - (I_{1}-I_{2})\omega_{1}\omega_{2} = \tau_{3} . \tag{4.5.8}\label{eq:4.5.8} \]

Estos toman el lugar de los\( \tau = I \dot{\omega}\) cuales estamos más familiarizados en problemas elementales en los que un cuerpo gira alrededor de un eje principal y se aplica un par alrededor de ese eje principal.

Si no hay pares externos que actúen sobre el cuerpo, entonces tenemos las Ecuaciones de Euler de rotación libre de un cuerpo rígido:

\[ \ I_{1}\dot{\omega_{1}} = (I_{2}-I_{3})\omega_{2}\omega_{3} , \tag{4.5.9}\label{eq:4.5.9} \]

\[ \ I_{1}\dot{\omega_{2}} = (I_{3}-I_{1})\omega_{3}\omega_{1} , \tag{4.5.10}\label{eq:4.5.10} \]

\[ \ I_{3}\dot{\omega_{3}} = (I_{1}-I_{2})\omega_{1}\omega_{2} . \tag{4.5.11}\label{eq:4.5.11} \]

Ejemplo\(\PageIndex{1}\)

En el dibujo anterior, una lámina rectangular está girando con velocidad angular constante\(\boldsymbol\omega\) entre dos rodamientos sin fricción. Le vamos a aplicar las Ecuaciones de movimiento de Euler. Encontraremos que los rodamientos están ejerciendo un par sobre el rectángulo, y el rectángulo está ejerciendo un par sobre los cojinetes. El momento angular del rectángulo no es constante — al menos no es constante en dirección. Calcularemos el par (su magnitud y su dirección) y veremos qué está sucediendo con el momento angular.

Observamos que los principales (segundos) momentos de inercia son

\( I_{1} = \frac{1}{3}mb^{2} \qquad I_{2} = \frac{1}{3}ma^{2} \qquad I_{3} = \frac{1}{3}m(a^{2} +b^{2})\)

y que los componentes de la velocidad angular son

\( \omega_{1} = \omega \cos \theta \qquad \omega_{2} = \omega \sin \theta \qquad \omega_{3} = 0.\)

Además,\(\dot{\boldsymbol\omega}\) y todos sus componentes son cero. Inmediatamente obtenemos, de las ecuaciones de Euler, que\( \tau_{1}\) y\( \tau_{2}\) son cero, y que el par ejercido sobre el rectángulo por los cojinetes es

\( \tau_{3} = (I_{2}-I_{1})\omega_{1}\omega_{2} = \frac{1}{3}m(a^{2}-b^{2})\omega^{2}sin \theta \cos \theta\)

Y desde

\( \sin \theta = \frac{b}{\sqrt{a^{2} +b^{2}}} \quad and \quad \cos \theta = \frac{b}{\sqrt{a^{2} +b^{2}}},\)

obtenemos

\( \tau_{3} = \frac{m(a^{2} - b^{2})ab}{3(a^{2} + b^{2})}\omega^{2}\)

Así\( \boldsymbol\tau \), el par ejercido sobre el rectángulo por los cojinetes se dirige normal al plano del rectángulo (fuera del plano del papel en la instantánea instantánea anterior).

El momento angular viene dado por\( { \bf L} = {\bf l} \boldsymbol\omega \). Es decir:

\( \left(\begin{array}{c}L_{1}\\ L_{2}\\L_{3}\end{array}\right) = \frac{1}{3}m\left(\begin{array}{c}b^{2} \quad 0 \quad 0\\ 0 \quad a^{2} \quad 0 \\ 0 \quad 0 \quad a^{2}+b^{2}\end{array}\right)\left(\begin{array}{c}\omega \cos \theta\\ \omega \sin \theta \\ 0\end{array}\right) \)

\( L_{1} = \frac{1}{3}mb^{2}\omega \cos \theta = \frac{1}{3}m\frac{ab^{2}}{\sqrt{a^{2}+b^{2}}}\omega \)

\( L_{2} = \frac{1}{3}mb^{2}\omega \sin \theta = \frac{1}{3}m\frac{ab^{2}}{\sqrt{a^{2}+b^{2}}}\omega \)

\( L_{3} = 0 \)

\( L = \frac{1}{3} mab \omega \)

\( L_{2}/ L_{1} = \frac{a^{2}sin \theta}{b^{2}cos \theta} = \cot \theta = tan(90° - \theta) \)

Esto nos dice que\( \bf L \) está en el plano del rectángulo, y hace un ángulo de 90° -\( \theta \) con el\( x\) eje -, o q con el\( y\) -eje, y gira alrededor del vector\( \boldsymbol\tau \). \( \boldsymbol\tau \)es perpendicular al plano del rectángulo, y por supuesto el cambio de adentro\( \bf L \) tiene lugar en esa dirección. El par no funciona,\( \boldsymbol\omega \) y\( T\) son constantes. El lector podría encontrar una analogía en la situación de un planeta en órbita alrededor del Sol en una órbita circular.. El planeta experimenta una fuerza que siempre es perpendicular a su velocidad. La fuerza no funciona, y la velocidad y la energía cinética permanecen constantes.

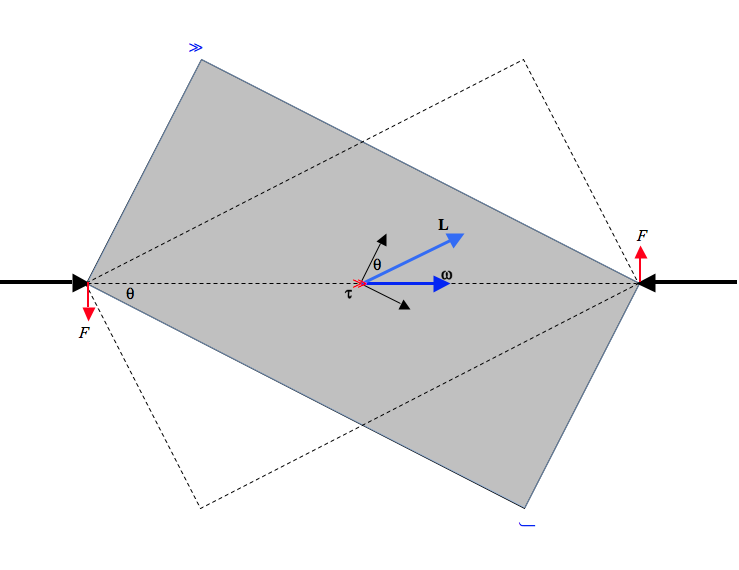
El par en la placa se puede representar como un par de fuerzas ejercidas por los cojinetes sobre la placa, cada una de magnitud\( \frac{\tau_{3}}{2\sqrt{a^{2} + b^{2}}}, \) o\( \frac{m(a^{2}-b^{2})}{6(a^{2}-b^{2})^\frac{3}{2}}\omega^{2} \) Las fuerzas ejercidas por la placa sobre los cojinetes están, por supuesto, en la dirección opuesta.

Ejemplo\(\PageIndex{2}\)

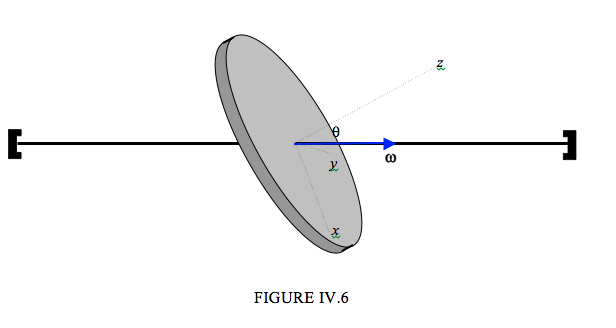
La Figura IV.6 muestra un disco de masa\( m\), radio\( a\), girando a una velocidad angular constante\( \omega\) alrededor de un eje que está inclinado en ángulo\( \theta \) con la normal al disco. He dibujado tres ejes principales fijos al cuerpo. Los ejes\( x\) - y\( y\) - están en el plano del disco\ negrita símbolo; la dirección del\( x\) -eje se elige para que el eje (y por lo tanto el vector\( \boldsymbol\omega \)) esté en el\( zx\) -plano. El disco está evidentemente desequilibrado y debe haber un par sobre él para mantener el movimiento.

Dado que\( \boldsymbol\omega \) es constante, todos los componentes de\( \dot{ \boldsymbol\omega} \) son cero, por lo que las ecuaciones de Euler son

\( \tau_{1}= (I_{3} - I_{2})\omega_{3}\omega_{2}, \)

\( \tau_{2}= (I_{1} - I_{3})\omega_{1}\omega_{3}, \)

\( \tau_{3}= (I_{2} - I_{1})\omega_{2}\omega_{1}, \)

Ahora\( \omega_{1} = \omega \sin \theta , \omega_{2} = \omega \cos \theta , I_{1} = \frac{1}{4} ma^{2} , I_{2} = \frac{1}{4} ma^{2}, I_{3} = \frac{1}{1} ma^{2} \)

Por lo tanto\( \tau_{1} = \tau_{3} = 0, and \tau_{2} = - \frac{1}{4}ma^{2}\omega ^{2}sin\theta cos\theta = -\frac{1}{8}ma^{2}\omega^{2}sin2\theta \)

(Compruebe, como siempre, que esta expresión sea dimensionalmente correcta). Así, el par que actúa sobre el disco está en la\( y\) dirección negativa.

¿Se puede conciliar el hecho de que hay un par que actúa sobre el disco con el hecho de que se mueve con velocidad angular constante? ¡Sí, lo más decididamente! Lo que no es constante es el momento angular\( \bf{L}\), que se mueve alrededor del eje en un cono tal que\( \dot{\bf L} = -\tau_{2} { \bf j} \), donde\( \bf{j}\) está el vector unitario a lo largo del\( y\) eje -eje.