4.5: Precesión inducida por par

La dinámica de rotación se vuelve aún más compleja ante la presencia de fuerzas externas. Consideremos el efecto más importante y contradictorio de la precesión inducida por par, para el caso más simple de un cuerpo axialmente simétrico (que es un caso particular de la parte superior simétrica,\(I_{1}=I_{2} \neq I_{3}\)), soportado en algún punto A de su eje de simetría, que no coincide con el centro de masa 0 - ver Figura\(9 .\)

Figura 4.9. Parte superior simétrica en el campo de gravedad: (a) una vista lateral en el sistema y (b) la vista superior en la evolución de la componente horizontal del vector de momento angular.

El campo de gravedad uniforme\(\mathbf{g}\) crea fuerzas distribuidas en masa que, como sabemos por el análisis del péndulo físico en la Sec. 3, son equivalentes a una sola fuerza\(M \mathbf{g}\) aplicada en el centro de masa - en la Figura 9, punto 0. El par de esta fuerza en relación con el punto de soporte\(\mathrm{A}\) es\[\boldsymbol{\tau}=\left.\mathbf{r}_{0}\right|_{\text {in } \mathrm{A}} \times M \mathbf{g}=M l \mathbf{n}_{3} \times \mathbf{g} .\]

De ahí que la ecuación general (33) de la evolución del momento angular (válida en cualquier marco inercial, por ejemplo el que tiene un origen en el punto A) se convierte\[\dot{\mathbf{L}}=M l \mathbf{n}_{3} \times \mathbf{g} .\] A pesar de la aparente simplicidad de esto (¡exacto!) , su análisis es sencillo solo en el límite cuando la parte superior se lanza girando alrededor de su eje de simetría\(\mathbf{n}_{3}\) con una velocidad angular muy alta\(\omega_{\text {rot. }}\). En este caso, podemos descuidar la contribución a\(\mathbf{L}\) debido a una velocidad de precesión relativamente pequeña\(\omega_{\text {pre }}\) (aún por calcular), y usar la Eq. (26) para escribir\[\mathbf{L}=I_{3} \boldsymbol{\omega}=I_{3} \omega_{\mathrm{rot}} \mathbf{n}_{3} .\] Entonces la Eq. (70) muestra que el vector\(\mathbf{L}\) es perpendicular a ambos\(\mathbf{n}_{3}\) (y por lo tanto\(\mathbf{L}\)) y\(\mathbf{g}\), es decir, se encuentra dentro del plano horizontal y es perpendicular a la componente horizontal\(\mathbf{L}_{x y}\) del vector\(\mathbf{L}-\) ver Figura\(9 \mathrm{~b}\). Dado que, según la Ec. (70), la magnitud de este vector es constante,\(|\mathbf{L}|=m g l \sin \theta\), el vector\(\mathbf{L}\) (y por lo tanto el eje principal del cuerpo) gira alrededor del eje vertical con la siguiente velocidad angular:

\(\begin{aligned}&\text { Torque- } \\&\text { induced } \\&\text { ecession: } \\&\text { fintion } \\&\text { limit }\end{aligned} \quad \omega_{\text {pre }}=\frac{|\dot{\mathbf{L}}|}{L_{x y}}=\frac{M g l \sin \theta}{L \sin \theta} \equiv \frac{M g l}{L}=\frac{M g l}{I_{3} \omega_{\text {rot }}} .\)

Así, muy contra-intuitivamente, la parte superior de rotación rápida no sigue la fuerza externa, vertical y, además de girar rápidamente alrededor del eje de simetría\(\mathbf{n}_{3}\), realiza una revolución, llamada precesión inducida por par, alrededor del eje vertical. Nótese que, de manera similar a la frecuencia de precesión libre (59), la frecuencia de precesión inducida por par\((72)\) no depende del ángulo inicial (y sostenido)\(\theta\). Sin embargo, la frecuencia de precesión inducida por par es inversamente (en lugar de directamente) proporcional a\(\omega_{\text {rot }}\). Este hecho hace que la teoría simple anterior sea válida en muchos casos prácticos. En efecto, la Ec. (71) es cuantitativamente válida si la contribución de la precesión en\(\mathbf{L}\) es relativamente pequeña:\(I \omega_{\text {pre }} \ll I_{3} \omega_{\text {rot }}\), donde\(I\) está cierto momento efectivo de inercia para la precesión -que se calculará a continuación. Usando la Ec. (72), esta condición puede ser reescrita como\[\omega_{\mathrm{rot}}>>\left(\frac{M g l I}{I_{3}^{2}}\right)^{1 / 2} .\] Según la Ec. (16), para un cuerpo de proporciones no demasiado extremas, es decir, con todas las dimensiones lineales del orden de la misma escala de longitud\(l\), todos los momentos de inercia son del orden de\(M l^{2}\), de manera que el lado derecho de la Eq. \((73)\)es del orden de\((g / l)^{1 / 2}\), es decir, comparable con la frecuencia de pequeñas oscilaciones del mismo cuerpo que el péndulo físico, es decir, a la ausencia de su rápida rotación.

Para desarrollar una teoría cualitativa que fuera válida más allá de dicho tratamiento aproximado, se pueden utilizar las ecuaciones de Euler (66), pero no son muy convenientes. Un mejor enfoque, sugerido por el mismo L. Euler, es introducir un conjunto de tres ángulos independientes entre los ejes principales\(\left\{\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}_{3}\right\}\) unidos al cuerpo rígido, y los ejes\(\left\{\mathbf{n}_{x}, \mathbf{n}_{y}, \mathbf{n}_{z}\right\}\) de un marco de referencia inercial (Figura 10), para luego expresar la ecuación básica (33) de rotación, a través de estos ángulos. Existen varias opciones posibles para la definición de dichos ángulos; la Figura 10 muestra el conjunto de ángulos de Euler, más convenientes para análisis de rotación rápida. \({ }^{18}\)Como se puede ver, el primer ángulo de Euler,\(\theta\), es el ángulo polar habitual medido desde el\(\mathbf{n}_{z}\) eje -eje hasta el\(\mathbf{n}_{3}\) eje -eje. El segundo es el ángulo azimutal\(\varphi\), medido desde el\(\mathbf{n}_{x}\) eje -eje hasta la llamada línea de nodos formada por la intersección de planos\(\left[\mathbf{n}_{x}, \mathbf{n}_{y}\right]\) y\(\left[\mathbf{n}_{1}, \mathbf{n}_{2}\right]\). El último ángulo de Euler\(\psi\),, se mide Euler dentro del plano\(\left[\mathbf{n}_{1}, \mathbf{n}_{2}\right]\), desde la línea de nodos hasta el\(\mathbf{n}_{1}\) eje-eje. Por ejemplo, en el cuadro simple de precesión lenta inducida por la fuerza de una parte superior simétrica, que se discutió anteriormente, el ángulo\(\theta\) es constante, el ángulo\(\psi\) cambia rápidamente, con la velocidad de rotación\(\omega_{\mathrm{rot}}\), mientras que el ángulo\(\varphi\) evoluciona con la frecuencia de precesión\(\omega_{\text {pre }}(72)\).

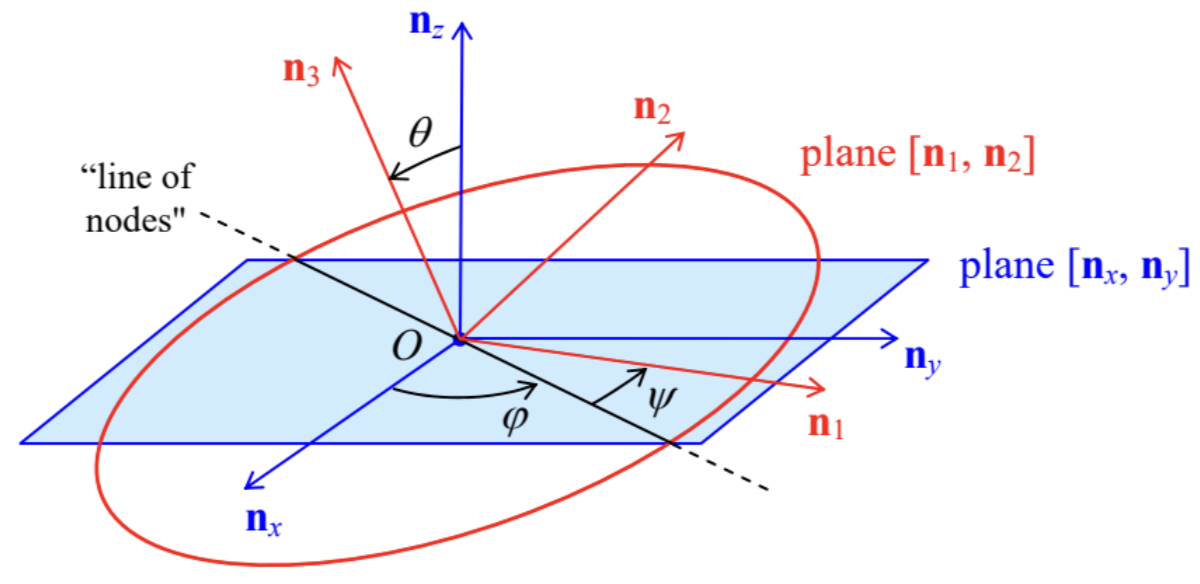Fig. 4.10. Definición de los ángulos de Euler.

Ahora podemos expresar los componentes de ejes principales del vector de velocidad angular instantánea, y\(\omega_{1}, \omega_{2}\)\(\omega_{3}\), como se mide en el marco de referencia de laboratorio, en términos de los ángulos de Euler. Esto se puede hacer fácilmente calculando, a partir de la Figura 10, las contribuciones de la evolución de los ángulos de Euler a la rotación alrededor de cada eje principal, y luego sumarlas:\[\begin{aligned} &\omega_{1}=\dot{\varphi} \sin \theta \sin \psi+\dot{\theta} \cos \psi \\ &\omega_{2}=\dot{\varphi} \sin \theta \cos \psi-\dot{\theta} \sin \psi \\ &\omega_{3}=\dot{\varphi} \cos \theta+\dot{\psi} \end{aligned}\] Estas relaciones permiten la expresión de la energía cinética de rotación\((25)\) y los componentes de momento angular (26) vía las coordenadas generalizadas\(\theta, \varphi\),\(\psi\) y sus derivadas del tiempo (es decir, las velocidades generalizadas correspondientes), y luego usar el poderoso formalismo lagrangiano para derivar sus ecuaciones de movimiento. Esto es especialmente sencillo de hacer en el caso de tops simétricos (con\(I_{1}=I_{2}\)), ya que al enchufar las ecuaciones (74) a la ecuación (25) obtenemos una expresión,\[T_{\text {rot }}=\frac{I_{1}}{2}\left(\dot{\theta}^{2}+\dot{\varphi}^{2} \sin ^{2} \theta\right)+\frac{I_{3}}{2}(\dot{\varphi} \cos \theta+\dot{\psi})^{2},\] que no incluye explícitamente\(\varphi\) ni tampoco\(\psi\). (Esto refleja el hecho de que para una parte superior simétrica siempre podemos seleccionar el\(\mathbf{n}_{1}\) -eje para que coincida con la línea de nodos, y de ahí tomar\(\psi=0\) en el momento considerado del tiempo. Tenga en cuenta que este truco no significa que podamos tomar\(\dot{\psi}=0\), porque el\(\mathbf{n}_{1}\) eje -eje, como se observa desde un marco de referencia inercial, se mueve!) Ahora no debemos olvidar que a la precesión inducida por par, el centro de masa también se mueve (ver, por ejemplo, la Figura 9), de manera que según la Ecuación (14), la energía cinética total del cuerpo es la suma de dos términos,\[T=T_{\text {rot }}+T_{\text {tran }}, \quad T_{\text {tran }}=\frac{M}{2} V^{2}=\frac{M}{2} l^{2}\left(\dot{\theta}^{2}+\dot{\varphi}^{2} \sin ^{2} \theta\right),\] mientras que su energía potencial es justa\[U=M g l \cos \theta+\text { const } \text {. }\] Ahora podríamos escribir fácilmente el Lagrange ecuaciones de movimiento para los ángulos de Euler, pero es más sencillo notar inmediatamente que según las ecuaciones (75) - (77), la función lagrangiana,\(T-U\), no depende explícitamente de las coordenadas “cíclicas”\(\varphi\) y\(\psi\), para que se conserven los momentos generalizados correspondientes (2.31): \[\begin{gathered} p_{\varphi} \equiv \frac{\partial T}{\partial \dot{\varphi}}=I_{\mathrm{A}} \dot{\varphi} \sin ^{2} \theta+I_{3}(\dot{\varphi} \cos \theta+\dot{\psi}) \cos \theta=\mathrm{const}, \\ p_{\psi} \equiv \frac{\partial T}{\partial \dot{\psi}}=I_{3}(\dot{\varphi} \cos \theta+\dot{\psi})=\mathrm{const}, \end{gathered}\]donde\(I_{\mathrm{A}} \equiv I_{1}+M l^{2}\). (Según la Ec. (29),\(I_{\mathrm{A}}\) es solo el momento de inercia del cuerpo para la rotación alrededor de un eje horizontal que pasa por el punto de soporte A.) Según la última de las ecuaciones (74),\(p_{\psi}\) es justa, es decir\(L_{3}\), la componente del momento angular a lo largo del eje de precesión\(\mathbf{n}_{3}\). Por otro lado, por su propia definición (78),\(p_{\varphi}\) es decir\(L_{z}\), el mismo componente\(\mathbf{L}\) del vector a lo largo del eje estático\(z\). (En realidad, podríamos prever de antemano la conservación de ambos componentes de\(\mathbf{L}\) para nuestro sistema, ya que el vector (69) del par externo es perpendicular a ambos\(\mathbf{n}_{3}\) y\(\mathbf{n}_{z}\).) Usando esta notación, y resolviendo el sistema simple de ecuaciones lineales (78) - (79) para las derivadas de ángulo, obtenemos\[\dot{\varphi}=\frac{L_{z}-L_{3} \cos \theta}{I_{\mathrm{A}} \sin ^{2} \theta}, \quad \dot{\psi}=\frac{L_{3}}{I_{3}}-\frac{L_{z}-L_{3} \cos \theta}{I_{\mathrm{A}} \sin ^{2} \theta} \cos \theta .\] Una cantidad más conservada en este problema es la energía mecánica completa\({ }^{19}\)\[E \equiv T+U=\frac{I_{\mathrm{A}}}{2}\left(\dot{\theta}^{2}+\dot{\varphi}^{2} \sin ^{2} \theta\right)+\frac{I_{3}}{2}(\dot{\varphi} \cos \theta+\dot{\psi})^{2}+M g l \cos \theta \text {. }\] Tapando Eqs. (80) en la Eq. (81), obtenemos una ecuación diferencial de primer orden para el ángulo\(\theta\), que puede representarse en la siguiente forma físicamente transparente:\[\frac{I_{\mathrm{A}}}{2} \dot{\theta}^{2}+U_{\mathrm{ef}}(\theta)=E, \quad U_{\mathrm{ef}}(\theta) \equiv \frac{\left(L_{z}-L_{3} \cos \theta\right)^{2}}{2 I_{\mathrm{A}} \sin ^{2} \theta}+\frac{L_{3}^{2}}{2 I_{3}}+M g l \cos \theta+\text { const }\] Así, de manera similar a los problemas planetarios considerados en la Sec. 3.4, se ha reducido la precesión inducida por par de un tope simétrico (¡sin aproximaciones!) a un problema 1D del movimiento de uno de sus grados de libertad, el ángulo polar\(\theta\), en el potencial efectivo\(U_{\mathrm{ef}}(\theta)\). De acuerdo con la Ec. (82), muy similar a la ecuación (3.44) para el problema planetario, este potencial es la suma de la energía potencial real\(U\) dada por la ecuación (77), y una contribución de la energía cinética del movimiento a lo largo de otros dos ángulos. En ausencia de rotación alrededor de los ejes\(\mathbf{n}_{z}\) y\(\mathbf{n}_{3}\) (i.e.,\(L_{z}=L_{3}=0\)), la Eq. (82) se reduce a la primera integral de la ecuación (40) de movimiento de un péndulo físico, con\(I^{\prime}=I_{\mathrm{A}}\). Si la rotación está presente, entonces (además del caso de condiciones iniciales muy especiales cuando\(\theta(0)=0\) y\(\left.L_{z}=L_{3}\right),{ }^{20}\) la primera contribución a\(U_{\mathrm{ef}}(\theta)\) diverge en\(\theta \rightarrow 0\) y\(\pi\), para que la energía potencial efectiva tenga un mínimo en algún valor distinto\(\theta_{0}\) de cero del ángulo polar \(\theta\)- ver Figura 11.

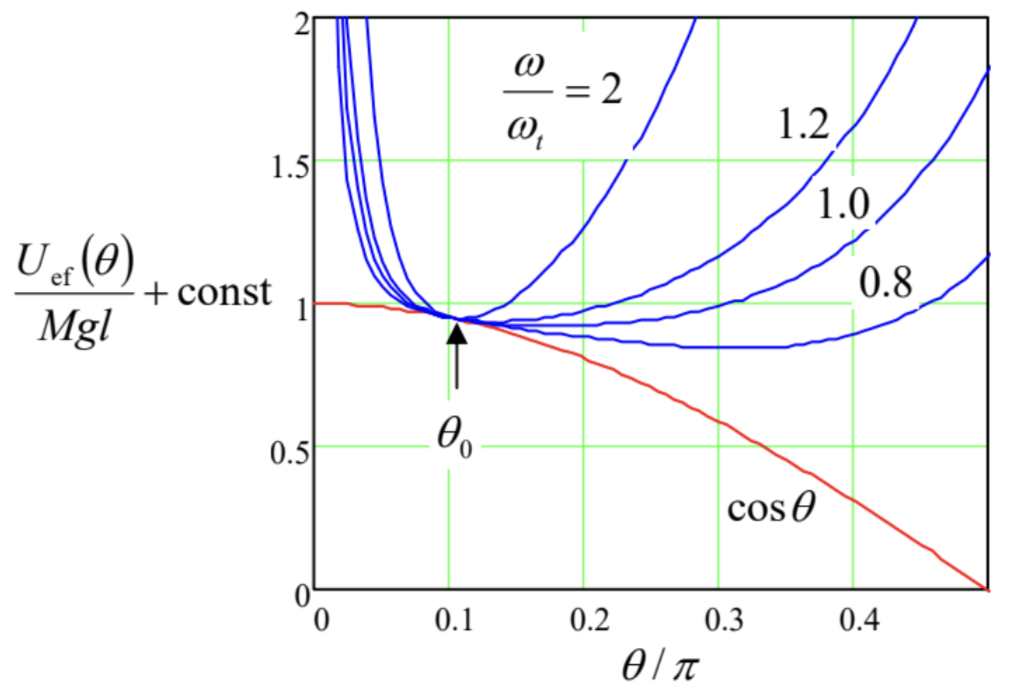
Figura 4.11. La energía potencial efectiva\(U_{\text {ef }}\) de la parte superior simétrica, dada por la Ec. (82), en función del ángulo polar\(\theta\), para un valor particular (0.95) de la relación\(r \equiv L_{z} / L_{3}\) (de manera que at\(\omega_{\text {rot }}>>\)\(\left.\omega_{\mathrm{h}}, \theta_{0}=\cos ^{-1} r \approx 0.1011 \pi\right)\), y varios valores de la relación\(\omega_{\mathrm{rot}} / \omega_{\mathrm{th}}\).

Si el ángulo inicial\(\theta(0)\) es igual a este valor\(\theta_{0}\), es decir, si la energía efectiva inicial es igual a su valor mínimo\(U_{\mathrm{ef}}\left(\theta_{0}\right)\), el ángulo polar permanece constante a través del movimiento:\(\theta(t)=\theta_{0}\). Esto corresponde a la precesión pura inducida por par cuya velocidad angular viene dada por la primera de las ecuaciones (80):\[\omega_{\mathrm{pre}} \equiv \dot{\varphi}=\frac{L_{z}-L_{3} \cos \theta_{0}}{I_{\mathrm{A}} \sin ^{2} \theta_{0}} .\] La condición para encontrar\(\theta_{0}, d U_{\mathrm{ef}} / d \theta=0\), es una ecuación algebraica trascendental que no se puede resolver analíticamente para parámetros arbitrarios. Sin embargo, en el límite de velocidad de giro alto (73), esto es posible. En efecto, en este límite la contribución\(M g l\) proporcional a\(U_{\text {ef }}\) es pequeña, y podemos analizar su efecto por aproximaciones sucesivas. En la\(0^{\text {th }}\) aproximación, es decir\(M g l=0\), at, el mínimo de\(U_{\text {ef }}\) se logra evidentemente en\(\cos \theta_{0}=L_{z} / L_{3}\), volviéndose la frecuencia de precesión (83) a cero. En la siguiente,\(1^{\text {st }}\) aproximación, podemos requerir que at\(\theta=\theta_{0}\), la derivada del primer término de la ecuación (82) para\(U_{\text {ef }}\) más\(\cos \theta\), igual a\(L_{z}\left(L_{z}-L_{3} \cos \theta\right) / I_{\mathrm{A}} \sin ^{2} \theta_{,}^{21}\) se cancele con la del término inducido por gravedad, igual a\(M g l\). Esto inmediatamente rinde\(\omega_{\text {pre }}=\left(L_{z}-L_{3} \cos \theta_{0}\right) / I_{\mathrm{A}} \sin ^{2} \theta_{0}=M g l / L_{3}\), de manera que\(\omega_{3} \equiv L_{3} / I_{3}\) identificándonos\(\omega_{\text {rot }}\) con (ver Figura 8), recuperamos la expresión simple (72).

El segundo resultado importante que se puede obtener fácilmente de la ecuación (82) es la expresión exacta para el valor umbral de la velocidad de giro para una parte superior giratoria verticalmente\(\left(\theta=0, L_{z}=L_{3}\right)\). De hecho, en el límite\(\theta \rightarrow 0\) esta expresión puede simplificarse fácilmente:\[U_{\text {ef }}(\theta) \approx \text { const }+\left(\frac{L_{3}^{2}}{8 I_{\mathrm{A}}}-\frac{M g l}{2}\right) \theta^{2} .\] Esta fórmula muestra que si\(\omega_{\mathrm{rot}} \equiv L_{3} / I_{3}\) es superior al siguiente valor umbral,

\[\ \text{Threshold rotation speed}\quad\quad\quad\quad\omega_{\mathrm{th}} \equiv 2\left(\frac{M g l I_{\mathrm{A}}}{I_{3}^{2}}\right)^{1 / 2},\]

entonces el coeficiente at\(\theta^{2}\) en la Ec. (84) es positivo, por lo que\(U_{\text {ef }}\) tiene un mínimo estable en\(\theta_{0}=0\). Por otro lado, si\(\omega_{3}\) se disminuye por debajo\(\omega_{\mathrm{th}}\), el punto fijo se vuelve inestable, de manera que la parte superior cae. Como muestran las gráficas de la Figura 11, la Ec. (85) para la frecuencia umbral funciona muy bien incluso para valores distintos de cero pero pequeños del ángulo de precesión\(\theta_{0}\). Tenga en cuenta que si tomamos\(I=I_{\mathrm{A}}\) en la condición\((73)\) del tratamiento aproximado, adquiere un sentido muy sencillo:\(\omega_{\mathrm{rot}}>>\omega_{\mathrm{th}}\).

Por último, las ecuaciones (82) dan una descripción natural de un fenómeno más. Si la energía inicial es mayor que\(U_{\mathrm{ef}}\left(\theta_{0}\right)\), el ángulo\(\theta\) oscila entre dos puntos de inflexión clásicos a ambos lados del punto fijo\(\theta_{0}\) -véase también la Figura 11. La ley y frecuencia de estas oscilaciones se pueden encontrar exactamente como en la Sec. \(3.3\)- ver Eq. (3.27) y (3.28). En\(\omega_{3} \gg \omega_{\mathrm{h}}\), este movimiento es una rotación rápida del eje de simetría\(\mathbf{n}_{3}\) del cuerpo alrededor de su posición promedio realizando la precesión lenta inducida por par. Históricamente, estas oscilaciones se llaman nutaciones, pero su física es similar a la de la libre precesión que se analizó en la sección anterior, y el orden de magnitud de su frecuencia viene dado por la Ec. (59).

Se puede probar que la pequeña fricción (no tomada en cuenta en el análisis anterior) conduce primero a la descomposición de estas nutaciones, luego a una deriva más lenta del ángulo de precesión\(\theta_{0}\) a cero y, finalmente, a una disminución gradual de la velocidad de giro\(\omega_{\mathrm{rot}}\) hasta que alcanza el umbral (85) y la parte superior cae.

---

\({ }^{19}\)De las diversas opciones más convenientes en ausencia de rotación rápida, la más común es el conjunto de los llamados ángulos Tait-Brian (llamados guiñada, cabeceo y balanceo), que se utilizan ampliamente para la navegación aérea y marítima.

\({ }^{20}\)En efecto, dado que el lagrangiano no depende del tiempo explícitamente,\(H=\) const, y dado que la energía cinética completa\(T\) (75) - (76) es una función cuadrática-homogénea de las velocidades generalizadas,\(E=H\).

\({ }^{21}\)En ese simple caso, el cuerpo sigue girando alrededor del eje de simetría vertical:\(\theta(t)=0\). Tenga en cuenta, sin embargo, que dicho movimiento es estable sólo si la velocidad de giro es suficientemente alta - véase la Ec. (85) a continuación.

\({ }^{22}\)En efecto, la derivada de la fracción\(1 / 2 I_{\mathrm{A}} \sin ^{2} \theta\), tomada en el punto\(\cos \theta=L_{z} / L_{3}\), se multiplica por el numerador\(\left(L_{z}-L_{3} \cos \theta\right)^{2}\), que se vuelve a cero en este punto.