4.7: Problemas de ejercicio

4.1. Calcule los momentos principales de inercia para los siguientes cuerpos rígidos uniformes:

(i) un aro delgado, plano, redondo, (ii) un disco redondo plano, (iii) un caparazón esférico delgado y (iv) una esfera sólida Compare los resultados, asumiendo que todos los cuerpos tienen el mismo radio\(R\) y masa\(M\).

4.2. Calcule los principales momentos de inercia para los cuerpos rígidos mostrados en la siguiente figura:

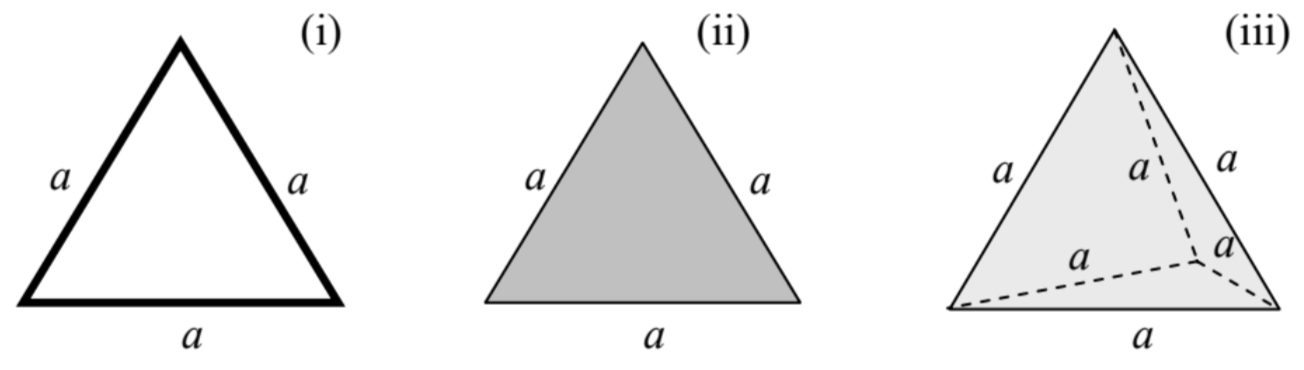
i) un triángulo equilátero hecho de varillas delgadas con una densidad de masa lineal uniforme\(\mu\),

(ii) una placa delgada en forma de triángulo equilátero, con una densidad de masa superficial uniforme\(\sigma\), y

\({ }^{32}\)Obsérvese que por la definición (1.36), los momentos angulares\(\mathbf{L}\) de las partículas se limitan a sumar. Como resultado, la forma final de la Ec. (102) es válida para un sistema arbitrario de partículas. iii) un tetraedro hecho de un material pesado con una densidad de masa aparente uniforme\(\rho\).

Suponiendo que la masa total de los tres cuerpos es la misma, comparar los resultados y dar una interpretación de su diferencia.

4.3. Demostrar que las ecuaciones (34) - (36) son válidas para la rotación de un cuerpo rígido alrededor de un eje fijo\(z\), aunque no pase por su centro de masa.

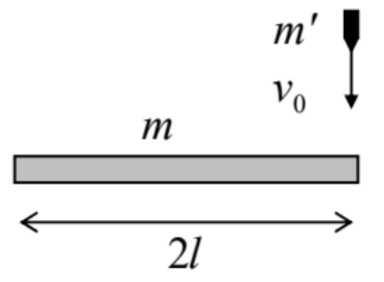
4.4. El extremo de una varilla delgada uniforme de longitud\(2 l\) y masa\(m\), inicialmente en reposo, es alcanzado por una bala de masa\(m^{\prime}\), volando con velocidad\(v_{0}\) (ver la figura de la derecha), que se atasca en la varilla. Utilice dos enfoques diferentes para calcular la velocidad del extremo opuesto de la varilla justo después de la colisión.

4.5. Una bola uniforme se coloca en un plano horizontal, mientras gira con una velocidad angular\(\omega_{0}\), pero sin velocidad lineal inicial. Calcular la velocidad angular después de que el deslizamiento de la bola se detenga, asumiendo la aproximación de Coulomb para la fuerza de fricción cinética:\(F_{f}=\mu N\), donde\(N\) es una presión entre las superficies, y\(\mu\) es un coeficiente independiente de la velocidad.

4.6. Un cuerpo puede girar alrededor de un eje horizontal fijo\(\mathrm{A}-\) ver Figura 5. Encuentra la frecuencia de sus pequeñas oscilaciones, en un campo de gravedad uniforme, en función de la distancia\(l\) del eje desde el centro de masa 0 del cuerpo, y analiza el resultado.

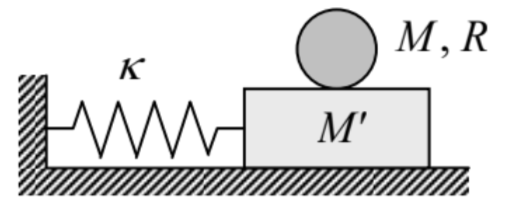
4.7. Calcular la frecuencia, y esbozar el modo de oscilaciones de un cilindro redondo uniforme de radio\(R\) y la masa\(M\), que puede rodar, sin deslizarse, sobre una superficie horizontal de un bloque de masa\(M\) '. El bloque, a su vez, puede moverse en la misma dirección, sin fricción, sobre una superficie horizontal, estando conectado a él con un resorte elástico - ver la figura a la derecha.

4.8. Una delgada barra uniforme de masa\(M\) y longitud\(l\) se cuelga de un hilo ligero de longitud\(l\) '(como una campana “campanilla” - ver la figura a la derecha). Derivar las ecuaciones de movimiento del sistema dentro del plano del dibujo.

4.9. Un cilindro de masa sólido, uniforme y redondo\(M\) puede rodar, sin deslizarse, sobre una superficie cilíndrica cóncava y redonda de un bloque de masa\(M^{\prime}\), en un campo de gravedad uniforme; vea la figura a la derecha. El bloque puede deslizarse sin fricción sobre una superficie horizontal. Utilizando el formalismo lagrangiano,

(i) encontrar la frecuencia de pequeñas oscilaciones del sistema cerca del equilibrio, y

(ii) bosquejar el modo de oscilación para el caso particular\(M^{\prime}=M, R^{\prime}=2 R\).

4.10. Un hemisferio sólido uniforme de radio\(R\) se coloca en un plano horizontal\(-\) ver la figura a la derecha. Encuentra la frecuencia de sus pequeñas oscilaciones dentro de un plano vertical, para dos casos finales:

(i) no hay fricción entre las superficies hemisféricas y planas, y

(ii) la fricción estática es tan fuerte que no hay deslizamiento entre estas superficies.

4.11. Para el problema de la “escalera deslizante”, iniciado en la Sec. 3 (ver Figura 7), encontrar el valor crítico\(\alpha_{\mathrm{c}}\) del ángulo\(\alpha\) en el que la escalera pierde su contacto con la pared vertical, asumiendo que comienza a deslizarse desde la posición vertical, con una velocidad inicial insignificante.

4.12. Seis varillas similares y uniformes de longitud\(l\) y masa\(m\) están conectadas por juntas ligeras para que puedan girar, sin fricción, una contra la otra, formando un polígono plano. Inicialmente, el polígono estaba en reposo, y tenía la forma hexagonal correcta\(-\) ver la figura a la derecha. De repente,\(\mathbf{F}\) se aplica una fuerza externa a la mitad de una varilla, en la dirección del centro de simetría del hexágono. Calcular las aceleraciones: de la varilla a la que se aplica la fuerza\((a)\), y de la varilla opuesta\(\left(a^{\prime}\right)\), inmediatamente después de la aplicación de la fuerza.

4.13. Un cuboide rectangular (paralelepípedo) con lados\(a_{1}, a_{2}\), y\(a_{3}\), hecho de un material con una densidad de masa constante\(\rho\), se gira, con una velocidad angular constante\(\omega\), alrededor de una de sus diagonales espaciales - ver la figura a la derecha. Calcular el par\(\tau\) necesario para sostener dicha rotación.

4.14. Un extremo de un eje ligero de longitud\(l\) está firmemente unido al centro de un disco sólido delgado y uniforme de radio\(R<<\)\(l\) y masa\(M\), cuyo plano es perpendicular al eje. Otro extremo del eje está unido a un eje vertical (ver la figura a la derecha) para que el eje pueda girar alrededor del eje sin fricción. El disco rueda, sin deslizamiento, sobre una superficie horizontal, de manera que todo el sistema gira alrededor del eje vertical con una velocidad angular constante\(\omega\). Calcular la fuerza de soporte (vertical)\(N\) ejercida sobre el disco por la superficie.

4.15. Un globo lleno de aire se coloca dentro de un contenedor lleno de agua, que se mueve por inercia en el espacio libre, a una gravedad insignificante. De repente,\(\mathbf{F}\) se aplica fuerza al contenedor, apuntando en cierta dirección. ¿En qué dirección se mueve el globo en relación con el contenedor?

4.16. Dos planetas están en órbita circular alrededor de su centro de masa común. Calcular la energía potencial efectiva de un cuerpo mucho más ligero (digamos, una nave espacial) que gira con la misma velocidad angular, en la línea que conecta los planetas. Esbozar la trama de la dependencia radial de\(U_{\text {ef }}\) y averiguar el número de los llamados puntos Lagrange es el cual la energía potencial tiene máximos locales. Calcular su posición explícitamente en el límite cuando uno de los planetas es mucho más masivo que el otro.

4.17. Un pequeño cuerpo se deja caer a la superficie de la Tierra desde la altura\(h<R_{\mathrm{E}}\), sin velocidad inicial. Calcular la magnitud y dirección de su desviación de la vertical, debido a la rotación de la Tierra. Estimar la magnitud del efecto para un cuerpo caído del Empire State Building. 4.18. Calcular la altura de las mareas solares en un océano grande, utilizando los siguientes supuestos simplificadores: el período de marea (\(1 / 2\)del día de la Tierra) es mucho más largo que el período de todas las olas del océano, la Tierra (de masa\(M_{\mathrm{E}}\)) es una esfera de radio\(R_{\mathrm{E}}\), y su\(r_{\mathrm{S}}\) distancia del Sol (de masa) \(M_{\mathrm{S}}\)) es constante y mucho mayor que\(R_{\mathrm{E}}\).

4.19. Una moneda de radio\(r\) se enrolla, con velocidad\(V\), sobre una superficie horizontal sin deslizamiento. ¿Cuál debería ser el ángulo de inclinación de la moneda\(\theta\) (ver la figura de la derecha) para que ruede en un círculo de radio\(R \gg>r\)? Modelando la moneda como un disco muy delgado y uniforme, y asumiendo que el ángulo\(\theta\) es pequeño, resuelve este problema en:

(i) un marco de referencia inercial (“lab”), y

(ii) el marco de referencia no inercial que se mueve con el centro de la moneda (pero que no gira con él).

4.20. Un satélite se encuentra en una órbita circular de radio\(R\), alrededor de la Tierra.

(i) Escribir las ecuaciones de movimiento de un cuerpo pequeño tal como se observa desde el satélite, y simplificarlas para el caso en que el movimiento se limite a las proximidades del satélite.

(ii) Utilizar las ecuaciones para probar que el cuerpo puede ser colocado en una trayectoria elíptica alrededor del centro de masa del satélite, dentro de su plano de rotación alrededor de la Tierra. Calcular la orientación y excentricidad de la elipse.

4.21. Una forma no esférica de un satélite artificial puede asegurar su orientación angular estable en relación con la superficie de la Tierra, ventajosa para muchos objetivos prácticos. Modelando el satélite como un cuerpo fuertemente alargado, axialmente simétrico, que se mueve alrededor de la Tierra en una órbita circular de radio\(R\), encuentra su orientación estable.

4.22. \({ }^{*}\)Una varilla rígida, recta y uniforme de longitud\(l\), con el extremo inferior sobre un pivote, cae en un campo de gravedad uniforme - ver la figura a la derecha. Descuidando la fricción, calcule la distribución del par de flexión\(\tau\) a lo largo de su longitud y analice el resultado.

Pista: El par de flexión es el par neto de la fuerza\(\mathbf{F}\) que actúa entre dos partes de la varilla, separadas mentalmente por su sección transversal, alrededor de un cierto “eje neutro”. \({ }^{33}\)Como se discutirá en detalle en la Sec. 7.5, en la definición adecuada de este eje, el gradiente del par de flexión a lo largo de la longitud de la varilla es igual a\((-F)\), donde\(F\) está el componente de barra normal (“cizallamiento”) de la fuerza ejercida por la parte superior de la varilla en su parte inferior.

4.23. \(\mathbf{r}\)Sea el vector de radio de una partícula, medido en un marco de referencia posiblemente no inercial pero ciertamente no giratorio. Tomando sus componentes cartesianos para las coordenadas generalizadas, calcular el impulso generalizado correspondiente\(\boldsymbol{\mu}\) de la partícula, y su función hamiltoniana\(H\). Comparar\(\boldsymbol{\mu}\) con\(m \mathbf{v}\), y\(H\) con la energía de la partícula\(E\). Derivar la ecuación lagrangiana del movimiento en este enfoque, y compararla con la Ec. (92).

---

\({ }^{34}\)Las definiciones inadecuadas de este par son la razón principal de numerosas soluciones erróneas de este problema, publicadas en línea - ¡cuidado con los lectores!