5.9: Problemas de ejercicio

5.1. Para un sistema con la función de respuesta dada por la Ec. (17), probar la Ec. (26) y utilizar un enfoque diferente al utilizado en la Sec. 1, para derivar la Ec. (34).

Consejo: Es posible que le guste usar el teorema integral de Cauchy y la fórmula integral de Cauchy para funciones analíticas de una variable compleja\({ }^{42}\)

5.2. Se ejerce un pulso de fuerza de onda cuadrada (ver la figura de la derecha) sobre un oscilador lineal con frecuencia propia\(\omega_{0}\) (sin amortiguación), inicialmente en reposo. Calcular la ley del movimiento\(q(t)\), esbozarla e interpretar el resultado.

5.3. At\(t=0\), una fuerza externa sinusoidal\(F(t)=F_{0} \cos \omega t\), se ejerce sobre un oscilador lineal con frecuencia propia\(\omega_{0}\) y amortiguación\(\delta\), que estaba en reposo en\(t \leq 0\).

(i) Derivar la expresión general para la evolución temporal de la coordenada del oscilador, e interpretar el resultado.

(ii) Deletrear el resultado para la resonancia exacta\(\left(\omega=\omega_{0}\right)\) en un sistema con baja amortiguación y\(\left(\delta<<\omega_{0}\right)\), en particular, explorar el límite\(\delta \rightarrow 0\).

5.4. Un pulso de fuerza externa\(F(t)\), con una duración finita\(\tau\), se ejerce sobre un oscilador lineal, inicialmente en reposo en su posición de equilibrio. Descuidando la disipación, calcule el cambio de energía del oscilador, utilizando dos enfoques diferentes, y compare los resultados.

5.5. Para un sistema con la siguiente función lagrangiana:\[L=\frac{m}{2} \dot{q}^{2}-\frac{\kappa}{2} q^{2}+\frac{\varepsilon}{2} \dot{q}^{2} q^{2},\] calcular la frecuencia de oscilaciones libres en función de su amplitud\(A\), at\(A \rightarrow 0\), utilizando dos enfoques diferentes.

5.6. Para un sistema con la función Lagrangiana\[L=\frac{m}{2} \dot{q}^{2}-\frac{\kappa}{2} q^{2}+\varepsilon \dot{q}^{4},\] con pequeño parámetro\(\varepsilon\), utilice el método van der Pol para encontrar la frecuencia de oscilaciones libres en función de su amplitud.

5.7. En el plano\(\left[a_{1}, a_{2}\right]\) de dos parámetros reales, independientes del tiempo\(a_{1}\) y\(a_{2}\), encontrar las regiones en las que el punto fijo del siguiente sistema de ecuaciones,\[\begin{aligned} &\dot{q}_{1}=a_{1}\left(q_{2}-q_{1}\right), \\ &\dot{q}_{2}=a_{2} q_{1}-q_{2}, \end{aligned}\] es inestable, y bosquejar las regiones de cada punto fijo tipo nodos\(-\) estables e inestables, enfoques, etc.

5.8. Resuelve el Problema 3 (ii) usando las ecuaciones reducidas (57), y compara el resultado con la solución exacta.

5.9. Utilice las ecuaciones reducidas para analizar oscilaciones forzadas en un oscilador con amortiguación no lineal débil, descrita por la siguiente ecuación:\[\ddot{q}+2 \delta \dot{q}+\omega_{0}^{2} q+\beta \dot{q}^{3}=f_{0} \cos \omega t,\] con\(\omega \approx \omega_{0} ; \beta, \delta>0\); y\(\beta \omega A^{2}<<1\). En particular, encontrar la amplitud estacionaria de las oscilaciones forzadas y analizar su estabilidad. Discutir el (los) efecto (s) del término no lineal sobre la resonancia.

5.10. Dentro del enfoque discutido en la Sec. 4, calcular la frecuencia promedio de un autooscilador fuera del rango de su bloqueo de fase por una fuerza sinusoidal externa.

5.11.* Utilice las ecuaciones reducidas para analizar la estabilidad de las oscilaciones forzadas no lineales descritas por la ecuación Duffing (43). Relacionar el resultado con la pendiente de las curvas de resonancia (Figura 4).

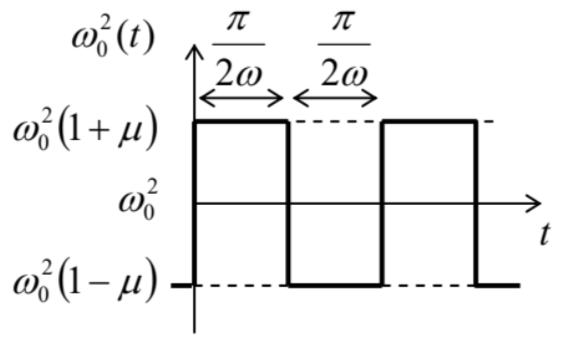
5.12. Utilice el método van der Pol para encontrar la condición de excitación paramétrica del oscilador descrita por la siguiente ecuación:\[\ddot{q}+2 \delta \dot{q}+\omega_{0}^{2}(t) q=0,\] donde\(\omega_{0}^{2}(t)\) está la función de onda cuadrada que se muestra en la figura de la derecha, con\(\omega \approx \omega_{0}\).

5.13. Utilizar el método van der Pol para analizar la excitación paramétrica de un oscilador con amortiguación no lineal débil, descrito por la siguiente ecuación:\[\ddot{q}+2 \delta \ddot{q}+\beta \dot{q}^{3}+\omega_{0}{ }^{2}(1+\mu \cos 2 \omega t) q=0 \text {, }\] con\(\omega \approx \omega_{0} ; \beta, \delta>0 ;\) y\(\mu, \beta \omega A^{2}<<1\). En particular, encontrar la amplitud de las oscilaciones estacionarias y analizar su estabilidad.

5.14. \({ }^{*}\)Añadiendo término no lineal\(\alpha q^{3}\) al lado izquierdo de la Ec. (75),

i) encontrar la suma correspondiente a las ecuaciones reducidas,

ii) calcular la amplitud estacionaria\(A\) de las oscilaciones paramétricas,

iii) encontrar el tipo y la estabilidad de cada punto fijo de las ecuaciones reducidas,

iv) esbozar los planos de fase Poincare del sistema en las principales regiones paramétricas.

5.15. Utilice el método van der Pol para encontrar la condición de excitación paramétrica de un oscilador con modulación débil tanto de la masa\(m(t)=m_{0}\left(1+\mu_{m} \cos 2 \omega t\right)\) efectiva como de la constante de resorte efectiva\(\kappa(t)=\kappa_{0}\left[1+\mu_{\kappa} \cos (2 \omega t-\psi)\right]\), con la misma frecuencia\(2 \omega \approx 2 \omega_{0}\), en relación de profundidades de modulación arbitraria\(\mu_{m} / \mu_{k}\) y desplazamiento de fase\(\psi\). Interpretar el resultado en términos de modulación de la frecuencia instantánea\(\omega(t) \equiv[\kappa(t) / m(t)]^{1 / 2}\) y la impedancia mecánica\(Z(t) \equiv[\kappa(t) m(t)]^{1 / 2}\) del oscilador.

5.16. \({ }^{*}\)Encuentra la condición de excitación paramétrica de un oscilador no lineal descrito por la siguiente ecuación:\[\ddot{q}+2 \delta \dot{q}+\omega_{0}^{2} q+\gamma q^{2}=f_{0} \cos 2 \omega t,\] con suficientemente pequeño\(\delta, \gamma, f_{0}\), y\(\xi \equiv \omega-\omega_{0}\).

5.17. Encuentra la condición de estabilidad del punto de equilibrio\(q=0\) de un oscilador paramétrico descrito por la Ec. (75), en el límite cuando\(\delta<<\left|\omega_{0}\right|<<\omega\) y\(\mu<<1\). Utilizar el resultado para analizar la estabilidad del péndulo Kapitza mencionado en la Sec. 5.

---

\({ }^{42}\)Véase, por ejemplo, MA Ec. (15.1).