6.4: Ondas Acústicas

Ahora volvamos al límite de las ondas acústicas de baja frecuencia, libres de dispersión, con\(|\omega|<<\omega_{0}\), propagándose con la velocidad independiente de la frecuencia (31). Tales ondas son propiedad general de cualquier medio elástico continuo y obedecen a una ecuación diferencial parcial simple (y muy importante). Para derivarlo, señalemos que en el límite de onda acústica,\(|k d|<<1,{ }^{11}\) el desplazamiento de fase\(\alpha \equiv k d\) está muy cerca de\(2 \pi n\). Esto significa que las diferencias\(q_{j+1}(t)-q_{j}(t)\) y\(q_{j}(t)-q_{j-1}(t)\), participando en la Ec. (25), son relativamente pequeñas y pueden aproximarse con\(\partial q / \partial j \equiv \partial q / \partial(z / d) \equiv d(\partial q / \partial z)\), con las derivadas tomadas en puntos medios entre las partículas: respectivamente,\(z_{+} \equiv\left(z_{j+1}-z_{j}\right) / 2\) y\(z_{-} \equiv\left(z_{j}-z_{j-1}\right) / 2\). Consideremos ahora\(z\) como argumento continuo, e introduzcamos al desplazamiento de partículas\(q(z, t)-\) una función continua del espacio y el tiempo, satisfaciendo el requerimiento\(q\left(z_{j}, t\right)=q_{j}(t)\). En esta notación, en el límite kd\(\rightarrow 0\), la suma de los dos últimos términos de la ecuación (24) se convierte\(-\kappa d\left[\partial q / \partial z\left(z_{+}\right)-\partial q / \partial z\left(z_{-}\right)\right]\), y por lo tanto puede aproximarse como\(-\kappa d^{2}\left(\partial^{2} q / \partial z^{2}\right)\), con la segunda derivada tomada en el punto\(\left(z_{+}-z_{-}\right) / 2 \equiv z_{j}\), es decir, exactamente en el mismo punto que la derivada de tiempo. Como resultado, todo el conjunto de ecuaciones diferenciales ordinarias (24), para diferentes\(j\), se reduce a una sola ecuación diferencial parcial\[m \frac{\partial^{2} q}{\partial t^{2}}-\kappa_{\text {ef }} d^{2} \frac{\partial^{2} q}{\partial z^{2}}=0 .\] Usando la ecuación (31), podemos reescribir esta ecuación de\(1 D\) onda de una forma más general\[\left(\frac{1}{v^{2}} \frac{\partial^{2}}{\partial t^{2}}-\frac{\partial^{2}}{\partial z^{2}}\right) q(z, t)=0\] La propiedad más importante de la ecuación de onda ( 40), que puede verificarse mediante una sustitución elemental, es que se satisface por cualquiera de dos soluciones de onda viajera (o su superposición lineal):\[q_{+}(z, t)=f_{+}(t-z / v), \quad q_{-}(z, t)=f_{-}(t+z / v),\] donde\(f_{\pm}\) están cualesquiera funciones suaves de un argumento. El sentido físico de estas soluciones puede revelarse al notar que los desplazamientos\(q_{\pm}\) no cambian al agregar un cambio arbitrario\(\Delta t\) a su argumento de tiempo, siempre que vaya acompañado de una adición de la adición proporcional de\(\mp v \Delta t\) a su argumento espacial. Esto significa que con el tiempo, las formas de onda simplemente se mueven (respectivamente, hacia la izquierda o hacia la derecha), con la velocidad constante\(v\), conservando su forma - ver Figura 7. \({ }^{12}\)

Fig. 6.7. Propagación de una onda viajera en un sistema 1D libre de dispersión.

Volviendo al modelo simple que se muestra en la Figura 4, permítanme enfatizar que la velocidad de la onda acústica\(v\) es diferente para las ondas de dos tipos: para las ondas longitudinales (con\(\kappa_{\mathrm{ef}}=\kappa\), ver Figura 4b),\[v=v_{l} \equiv\left(\frac{\kappa}{m}\right)^{1 / 2} d,\] mientras que para las ondas transversales (con\(\kappa_{\mathrm{ef}}=\mathscr{T} / d\), ver Figura 4c):\[v=v_{t}=\left(\frac{\mathscr{T}}{m d}\right)^{1 / 2} d \equiv\left(\frac{\mathscr{J} d}{m}\right)^{1 / 2} \equiv\left(\frac{\mathscr{T}}{\mu}\right)^{1 / 2}\] donde se encuentra constante\(\mu \equiv m / d\) tiene un sentido físico simple de la masa de la cadena de partículas por unidad de longitud. Evidentemente, estas velocidades, en un mismo sistema, pueden ser bastante diferentes.La ecuación de onda (40), con su único parámetro\(v\), puede ocultar el hecho de que cualquier sistema de soporte de ondas se caracteriza por un parámetro clave más. En nuestro modelo actual (Figura 4), este parámetro puede revelarse calculando las fuerzas\(F_{\pm}(z, t)\) que acompañan a cualquiera de las ondas viajeras (41) de los desplazamientos de partículas. Por ejemplo, en el límite de onda acústica\(k d \rightarrow 0\) que estamos considerando ahora, la fuerza ejercida por la\(j^{\text {th }}\) partícula sobre su vecino derecho puede aproximarse como\[F\left(z_{j}, t\right) \equiv \kappa_{\mathrm{ef}}\left[q_{j}(t)-q_{j+1}(t)\right] \approx-\left.\kappa_{\mathrm{ef}} \frac{\partial q}{\partial z}\right|_{z=z_{j}} d,\] donde, como se discutió anteriormente,\(\kappa_{\text {ef }}\) es igual\(\kappa\) para las ondas longitudinales, y\(\mathscr{T} / d\) para las transversales olas. Pero para las ondas viajeras (41), las derivadas parciales\(\partial q_{\pm} / \partial z\) son iguales a\(\mp\left(d f_{\pm} / d t\right) / v\), de manera que las fuerzas correspondientes son iguales a\[F_{\pm}=\mp \frac{\kappa_{\mathrm{ef}} d}{v} \frac{d f_{\pm}}{d t},\] es decir, son proporcionales a las velocidades de la partícula\(u=\partial q / \partial t\) en estas ondas\({ }^{13} u_{\pm}=d f_{\pm} / d t\),, para la misma\(z\) y t. \[\frac{F_{\pm}(z, t)}{u_{\pm}(z, t)}=-\kappa_{\mathrm{ef}} d \frac{\partial q_{\pm} / \partial z}{\partial q_{\pm} / \partial t}=-\kappa_{\mathrm{ef}} d \frac{\left(\mp d f_{\pm} / d t\right) / v}{d f_{\pm} / d t} \equiv \pm \frac{\kappa_{\mathrm{ef}} d}{v},\]depende solo de la dirección de propagación de la onda, pero es independiente de\(z\) y\(t\), y también de la forma de onda de propagación. Su magnitud,\[Z \equiv\left|\frac{F_{\pm}(z, t)}{u_{\pm}(z, t)}\right|=\frac{\kappa_{\mathrm{ef}} d}{v}=\left(\kappa_{\mathrm{ef}} m\right)^{1 / 2},\] que caracteriza la “rigidez” dinámica del sistema para las ondas propagadoras, se denomina impedancia de onda. \({ }^{14}\)Obsérvese que la impedancia está determinada por el producto de los parámetros genéricos del sistema\(\kappa_{\text {ef }}\) y\(m\), mientras que la velocidad de onda (31) es proporcional a su relación, de manera que estos dos parámetros son completamente independientes, y ambos son importantes. Según la Ec. (47), la impedancia de onda, al igual que la velocidad de onda, también es diferente para las ondas longitudinales y transversales:

\[\ Z_{l}=\frac{\kappa d}{\nu_{l}} \equiv(\kappa m)^{1 / 2}, \quad Z_{t}=\frac{\mathscr{T}}{\nu_{t}} \equiv(\mathscr{T} \mu)^{1 / 2}.\]

(Obsérvese que la primera de estas expresiones para\(Z\) coincide con la utilizada para un solo oscilador en la Sec. 5.6. En ese caso, también se\(Z\) puede refundir en una forma similar a la Ec. (46), es decir, como la relación de las amplitudes de fuerza y velocidad en oscilaciones libres.)

Una de las funciones clave de la impedancia de onda es escalar la potencia transportada por una onda viajera:\[\mathscr{P}_{\pm} \equiv F_{\pm}(z, t) u_{\pm}(z, t)=-\kappa_{\mathrm{ef}} d \frac{\partial q_{\pm}}{\partial z} \frac{\partial q_{\pm}}{\partial t}=\pm \frac{\kappa_{\mathrm{ef}} d}{v}\left(\frac{d f_{\pm}}{d t}\right)^{2} \equiv \pm Z\left(\frac{d f_{\pm}}{d t}\right)^{2} .\] Dos comentarios sobre este importante resultado. Primero, el signo de\(\mathscr{P}\) depende únicamente de la dirección de la propagación de la onda, pero no de la forma de onda. Segundo, el valor instantáneo de la potencia no cambia si nos movemos con la onda en cuestión, es decir, medimos\(\mathscr{P}\) en puntos con\(z \pm v t=\) const. Esto es natural porque en el sistema hamiltoniano que estamos considerando, se conserva la energía de las olas. Por lo tanto, la impedancia de onda\(Z\) caracteriza la transferencia de energía a lo largo del sistema en lugar de su disipación.

Otra función importante de la noción de impedancia de onda se hace evidente cuando consideramos las ondas en sistemas no uniformes. De hecho, nuestro análisis anterior asumió que el sistema 1D que soporta las ondas (Figura 4) es exactamente periódico, es decir, macroscópicamente uniforme, y se extiende desde\(-\infty\) hasta\(+\infty\). Ahora examinemos qué sucede cuando esto no es cierto. El ejemplo más simple y muy importante de tales sistemas no uniformes es una interfaz nítida, es decir, un punto (digamos,\(z=0\)) en el que los parámetros del sistema experimentan un salto mientras permanecen constantes en cada lado de la interfaz\(-\) ver Figura\(8 .\)

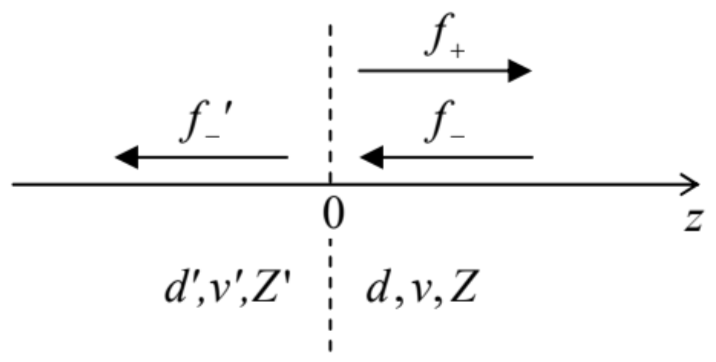Figura 6.8. Reflejo parcial de una onda desde una interfaz aguda.

En este caso, la ecuación de onda (40) y sus soluciones parciales (41) siguen siendo válidas para\(z\langle 0\) y\(z\rangle\) 0 - en el primer caso, con parámetros cebados. Sin embargo, el salto de parámetros en la interfaz conduce a una reflexión parcial de la onda incidente desde la interfaz, de manera que al menos en el lado de la incidencia (en el caso mostrado en la Figura 8, para\(z \geq 0\)), necesitamos usar dos términos de este tipo, uno describiendo la onda incidente y otro, el reflejado onda:\[q(z, t)= \begin{cases}f_{-}^{\prime}\left(t+z / v^{\prime}\right), & \text { for } z \leq 0, \\ f_{-}(t+z / v)+f_{+}(t-z / v), & \text { for } z \geq 0 .\end{cases}\] Para encontrar las relaciones entre las funciones\(f_{-}, f_{+}\), y\(f_{-}\) '(de las cuales la primera, que describe la onda incidente, puede considerarse conocida), podemos usar dos condiciones de límite en\(z=0\). Primero, el desplazamiento\(q_{0}(t)\) de la partícula en la interfaz tiene que ser el mismo si se considera parte del subsistema izquierdo o derecho, y participa en las ecuaciones (50) para ambos\(z \leq 0\) y\(z \geq 0\). Esto nos da la primera condición límite:\[f_{-}^{\prime}(t)=f_{-}(t)+f_{+}(t) .\] Por otro lado, las fuerzas ejercidas sobre la interfaz desde la izquierda y la derecha también deben tener la misma magnitud, ya que la interfaz puede considerarse como un objeto con una masa desaparecida, y cualquier fuerza neta distinta de cero le daría un infinito (y por lo tanto no física) aceleración. Junto con las ecuaciones (45) y (47), esto nos da la segunda condición límite:\[Z^{\prime} \frac{d f_{-}^{\prime}(t)}{d t}=Z\left[\frac{d f_{-}(t)}{d t}-\frac{d f_{+}(t)}{d t}\right] .\] Integrando ambas partes de esta ecuación a lo largo del tiempo, y descuidando la constante de integración (que describe un desplazamiento común de todas las partículas en lugar de sus oscilaciones), obtenemos\[Z^{\prime} f_{-}^{\prime}(t)=Z\left[f_{-}(t)-f_{+}(t)\right] .\] Ahora resolviendo el sistema de dos ecuaciones lineales (51) y (53) para\(f_{+}(t)\) y\(f_{+}^{\prime}(t)\), vemos que ambas funciones son proporcionales a la forma de onda incidente:\[f_{+}(t)=R f_{-}(t), \quad f_{-}^{\prime}(t)=\tau f_{-}(t),\] con los siguientes\((T)\) coeficientes de reflexión\((R)\) y transmisión:\[R=\frac{Z-Z^{\prime}}{Z+Z^{\prime}}, \quad \tau=\frac{2 Z}{Z+Z^{\prime}} .\] Más adelante en esta serie, veremos que con el adecuada redefinición de la impedancia, estas relaciones también son válidas para ondas de otra naturaleza física (incluyendo las ondas de Broglie en mecánica cuántica) que se propagan en estructuras continuas 1D, y también en continuas de dimensiones superiores, en la incidencia de onda normal sobre la interfaz. \({ }^{15}\)Tenga en cuenta que los coeficientes\(R\) y\(T\) dan las proporciones de amplitudes de onda, en lugar de sus potencias. Combinando las ecuaciones (49) y (55), obtenemos las siguientes relaciones para las potencias, ya sea en la interfaz o en los puntos correspondientes de las ondas reflejadas y transmitidas:\[\mathscr{P}_{+}=\left(\frac{Z-Z^{\prime}}{Z+Z^{\prime}}\right)^{2} \mathscr{P}_{-}, \quad \mathscr{P}_{-}^{\prime}=\frac{4 Z Z^{\prime}}{\left(Z+Z^{\prime}\right)^{2}} \mathscr{P}_{-} .\] Tenga en cuenta que\(\mathscr{P}_{-}+\mathscr{P}_{+}=\mathscr{P}_{-}^{\prime}\), nuevamente reflejando la conservación de energía de las olas.

Quizás el corolario más importante de las ecuaciones. (55) - (56) es que la onda reflejada desaparece completamente, es decir, la onda incidente se transmite completamente a través de la interfaz\(\left(\mathscr{P}_{+}^{\prime}=\mathscr{P}_{+}\right)\), si\(Z^{\prime}=Z\) se cumple la llamada condición de adaptación de impedancia, incluso si las velocidades de onda\(v(32)\) son diferentes en los lados izquierdo y derecho de la misma. Por el contrario, la igualdad de las velocidades acústicas en las dos continuas no garantiza la transmisión completa de su interfaz. Nuevamente, este es un resultado muy general.

Finalmente, señalemos que para el importante caso particular de una onda incidente sinusoidal:\({ }^{16}\)\[f_{-}(t)=\operatorname{Re}\left[a e^{-i \omega t}\right], \quad \text { so that } f_{+}(t)=\operatorname{Re}\left[\operatorname{Ra} e^{-i \omega t}\right],\] donde\(a\) está su amplitud compleja, la onda\((50)\) total a la derecha de la interfaz es\[q(z, t)=\operatorname{Re}\left[a e^{-i \omega(t+z / v)}+\operatorname{R} a e^{-i \omega(t-z / v)}\right] \equiv \operatorname{Re}\left[a\left(e^{-i k z}+\operatorname{Re}^{+i k z}\right) e^{-i \omega t}\right], \text { for } z \geq 0\] mientras que de acuerdo con la Ec. (45), la distribución de fuerza correspondiente es\[F(z, t)=F_{-}(z, t)+F_{+}(z, t)=-Z \frac{\partial f_{-}(t-z / v)}{\partial t}+Z \frac{\partial f_{-}(t-z / v)}{\partial t}=\operatorname{Re}\left[i \omega Z a\left(e^{-i k z}-R e^{+i k z}\right) e^{-i \omega t}\right] .\] Estas expresiones serán utilizadas en la siguiente sección.

---

\({ }^{11}\)Estrictamente hablando, según la discusión al final del apartado anterior, en este razonamiento\(k\) significa la distancia del número de onda desde el punto más cercano\(2 \pi n / d-\) ver Figura 5 nuevamente.

\({ }^{12}\)Desde el punto de vista de la Ec. (40), el único requisito para la “suavidad” de las funciones\(f_{\pm}\) es ser doblemente diferenciables. Sin embargo, no debemos olvidar que en nuestro caso la ecuación de onda es solo una aproximación de la ecuación discreta (24), de manera que de acuerdo con la ecuación (30), la conservación de la forma de onda viajera está limitada por la condición límite de onda acústica\(\omega<<\omega_{\max }\), que debe cumplirse para cualquier componente de Fourier de estas funciones .

\({ }^{13}\)Por supuesto, la velocidad de la partícula\(u\) (que es proporcional a la amplitud de onda) no debe confundirse con la velocidad de la onda\(v\) (que es independiente de esta amplitud).

\({ }^{14}\)Esta noción, con pesar, falta en muchos físicos (¡pero no en ingeniería!) libros de texto.

\({ }^{15}\)Ver, las partes correspondientes de las notas de conferencia: QM Sec. \(2.3\)y EM Sec. \(7.3\).

\({ }^{16}\)En el límite de onda acústica, cuando las impedancias\(Z\) y\(Z^{\prime}\), y por lo tanto el coeficiente de reflexión\(R\), son reales,\(R\) y\(Z\) pueden tomarse de debajo de los operadores Re en Ecuaciones (57) - (59). Sin embargo, en la forma actual, más general de estas relaciones también son válidas para el caso de frecuencias arbitrarias,\(\omega \sim \omega_{\max }\), cuando\(R\) y\(Z\) pueden ser complejas.