7.3: Ley de Hooke

Para formar un sistema completo de ecuaciones que describan la dinámica del continuo, es necesario complementar la ecuación (25) con una ecuación constitutiva apropiada que describa la relación entre las fuerzas descritas por el tensor de tensión\(\sigma_{i j}\), y las deformaciones\(\mathbf{q}\) descritas (en el pequeño límite de deformación) por el tensor de tensión\(s_{j j}\). Esta relación depende del medio, y generalmente puede ser bastante compleja. Incluso dejando solos diversos sólidos anisotrópicos (por ejemplo, cristales) y materiales macroscópicamenteinhomogéneos (como cerámica o arena), la deformación depende típicamente no solo del valor actual de la tensión (posiblemente de manera no lineal), sino también de la historia previa de aplicación de tensiones. De hecho, si la deformación excede un cierto umbral de plasticidad, los átomos (o nanocristales) pueden deslizarse a sus nuevas posiciones y nunca regresar incluso si la tensión se reduce. En consecuencia, las deformaciones se vuelven irreversibles - ver Figura 5.

Figura 7.5. Una relación típica entre la tensión y la deformación en sólidos (esquemáticamente).

Sólo por debajo de los umbrales de no linealidad y plasticidad (que suelen estar cerca unos de otros), la tensión es casi proporcional al estrés, es decir, obedece a la famosa ley de Hooke. \({ }^{8}\)Sin embargo, incluso en este rango elástico, la ley no es del todo simple, e incluso para un medio isotrópico se describe no por una sino por dos constantes, llamadas los módulos elásticos. La razón de ello es que la mayoría de los materiales elásticos resisten la deformación acompañada de un cambio de volumen (digamos, la compresión hidrostática) de manera diferente a cómo resisten una deformación por cizallamiento.

Para describir esta diferencia, primero representemos el tensor de deformación simétrica\((9 b)\) en la siguiente forma matemáticamente equivalente:\[s_{i j^{\prime}}=\left(s_{j j^{\prime}}-\frac{1}{3} \delta_{i j^{\prime}} \operatorname{Tr}(\mathrm{s})\right)+\left(\frac{1}{3} \delta_{j j^{\prime}} \operatorname{Tr}(\mathrm{s})\right) .\] De acuerdo con la Ec. (13), el tensor sin rastro en los primeros paréntesis de la Ec. (31) no da ninguna contribución al cambio de volumen, e.g., puede usarse para caracterizar una deformación puramente cortante, mientras que el segundo término describe solo la compresión hidrostática. Por lo tanto, podemos esperar que se pueda representar el tensor de tensión (¡nuevamente, solo dentro del rango de deformación elástica!) como\[\sigma_{i j^{\prime}}=2 \mu\left(s_{i j^{\prime}}-\frac{1}{3} \operatorname{Tr}(\mathrm{s}) \delta_{j j^{\prime}}\right)+3 K\left(\frac{1}{3} \operatorname{Tr}(\mathrm{s}) \delta_{j j^{\prime}}\right)\] donde\(K\) y\(\mu\) son constantes. (La inclusión de los coeficientes 2 y 3 en la Ec. (32) se justifica por la simplicidad de algunos de sus corolarios; véase, por ejemplo, las ecuaciones (36) y (41) a continuación.) En efecto, los experimentos muestran que la ley de Hooke en esta forma es seguida, a pequeña cepa, por todos los materiales isotrópicos. De acuerdo con la discusión anterior, la constante\(\mu\) (en algunos textos, denotada como\(G\)) se denomina módulo de cizallamiento, mientras que la constante\(K\) (a veces denotada\(B\)), el módulo volumétrico. Las dos columnas de la izquierda del Cuadro 1 muestran los valores aproximados de estos módulos para representantes típicos de varias clases principales de materiales. \({ }^{9}\)

Cuadro 7.1. Módulos elásticos, densidad y velocidades de sonido de unos pocos materiales representativos (valores aproximados)

	\(K(\mathrm{GPa})\)	\(\mu(\mathrm{GPa})\)	\(E(\mathrm{GPa})\)	\(v\)	\(\rho\left(\mathrm{kg} / \mathrm{m}^{3}\right)\)	\(v_{1}(\mathrm{~m} / \mathrm{s})\)	\(v_{\mathrm{t}}(\mathrm{m} / \mathrm{s})\)
Diamante\(^{(\mathrm{a})}\)	\ (K (\ mathrm {gPa})\)” style="text-align:center; ">600	\ (\ mu (\ mathrm {gPa})\)” style="text-align:center; ">450	\ (E (\ mathrm {gPa})\)” style="text-align:center; ">1.100	\ (v\)” style="text-align:center; ">\(0.20\)	\ (\ rho\ izquierda (\ mathrm {kg}/\ mathrm {m} ^ {3}\ derecha)\)” style="text-align:center; ">3.500	\ (v_ {1} (\ mathrm {~m}/\ mathrm {s})\)” style="text-align:center; ">1.830	\ (v_ {\ mathrm {t}} (\ mathrm {m}/\ mathrm {s})\)” style="text-align:center; ">1,200
Acero endurecido	\ (K (\ mathrm {gPa})\)” style="text-align:center; ">170	\ (\ mu (\ mathrm {gPa})\)” style="text-align:center; ">75	\ (E (\ mathrm {GPa})\)” style="text-align:center; ">200	\ (v\)” style="text-align:center; ">\(0.30\)	\ (\ rho\ izquierda (\ mathrm {kg}/\ mathrm {m} ^ {3}\ derecha)\)” style="text-align:center; ">7.800	\ (v_ {1} (\ mathrm {~m}/\ mathrm {s})\)” style="text-align:center; ">5.870	\ (v_ {\ mathrm {t}} (\ mathrm {m}/\ mathrm {s})\)” style="text-align:center; ">3.180
Agua\(^{(\mathrm{b})}\)	\ (K (\ mathrm {gPa})\)” style="text-align:center; ">\(2.1\)	\ (\ mu (\ mathrm {gPa})\)” style="text-align:center; ">0	\ (E (\ mathrm {gPa})\)” style="text-align:center; ">0	\ (v\)” style="text-align:center; ">\(0.5\)	\ (\ rho\ izquierda (\ mathrm {kg}/\ mathrm {m} ^ {3}\ derecha)\)” style="text-align:center; ">1,000	\ (v_ {1} (\ mathrm {~m}/\ mathrm {s})\)” style="text-align:center; ">1.480	\ (v_ {\ mathrm {t}} (\ mathrm {m}/\ mathrm {s})\)” style="text-align:center; ">0
Aire\(^{(\mathrm{b})}\)	\ (K (\ mathrm {gPa})\)” style="text-align:center; ">\(0.00010\)	\ (\ mu (\ mathrm {gPa})\)” style="text-align:center; ">0	\ (E (\ mathrm {gPa})\)” style="text-align:center; ">0	\ (v\)” style="text-align:center; ">\(0.5\)	\ (\ rho\ izquierda (\ mathrm {kg}/\ mathrm {m} ^ {3}\ derecha)\)” style="text-align:center; ">\(1.2\)	\ (v_ {1} (\ mathrm {~m}/\ mathrm {s})\)” style="text-align:center; ">332	\ (v_ {\ mathrm {t}} (\ mathrm {m}/\ mathrm {s})\)” style="text-align:center; ">0

a) Promedios sobre direcciones cristalográficas (10% anisotropía).

b) En la denominada\(\left(T=20^{\circ} \mathrm{C}, P=1\right.\) barra de condiciones ambientales\(\left.\equiv 10^{5} \mathrm{~Pa}\right)\).

Para apreciar mejor estos valores, primero discutamos el significado cuantitativo de\(K\) y\(\mu\), utilizando dos ejemplos simples de deformación elástica. Sin embargo, en preparación para eso, primero resolvamos el conjunto de nueve (o más bien seis diferentes) ecuaciones lineales (32) para\(s_{j j}\). Esto es fácil de hacer, debido a la estructura simple de estas ecuaciones: relacionan los componentes\(\sigma_{i j^{\prime}}\) y\(s_{i j^{\prime}}\) 'con los mismos índices, además de la implicación de la traza del tensor. Esta ligera complicación puede superarse fácilmente al notar que de acuerdo con la Ec. (32),\[\operatorname{Tr}(\sigma) \equiv \sum_{j=1}^{3} \sigma_{j j}=3 K \operatorname{Tr}(\mathrm{s}), \quad \text { so that } \operatorname{Tr}(\mathrm{s})=\frac{1}{3 K} \operatorname{Tr}(\sigma) .\] Conectando este resultado a la ecuación (32) y resolviéndolo para\(s_{j j}\), obtenemos fácilmente la relación recíproca, que puede ser representada en una forma similar:\[s_{i j^{\prime}}=\frac{1}{2 \mu}\left(\sigma_{j j^{\prime}}-\frac{1}{3} \operatorname{Tr}(\sigma) \delta_{j j^{\prime}}\right)+\frac{1}{3 K}\left(\frac{1}{3} \operatorname{Tr}(\sigma) \delta_{j j^{\prime}}\right) .\] Ahora apliquemos la ley de Hooke, en forma de Eqs. (32) o (34), a dos situaciones simples en las que los tensores de tensión y tensión se pueden encontrar sin usar la ecuación diferencial completa de la teoría de la elasticidad y las condiciones límite para ellos. (Ese será el tema de la siguiente sección.) La primera situación es la compresión hidrostática cuando el tensor de tensión es diagonal, y todos sus componentes diagonales son iguales - ver Ec. (19). \({ }^{10}\)Para este caso, la ecuación (34) rinde\[s_{j j^{\prime}}=-\frac{\mathcal{P}}{3 K} \delta_{j j^{\prime}},\] es decir, independientemente del módulo de cizallamiento, el tensor de deformación también es diagonal, con todos los componentes diagonales iguales. De acuerdo con las ecuaciones (11) y (13), esto significa que todas las dimensiones lineales del cuerpo se reducen en un factor similar, de manera que se conserva su forma, mientras que el volumen se reduce por\[\frac{\Delta V}{V}=\sum_{j=1}^{3} s_{j j}=-\frac{\mathcal{P}}{K} .\] Esta fórmula muestra claramente el sentido físico del módulo volumétrico\(K\) como la compresibilidad recíproca. Como muestra el Cuadro 1, los valores de\(K\) pueden ser dramáticamente diferentes para diversos materiales, e incluso para “materia blanda” como el agua este módulo es en realidad bastante alto. Por ejemplo, incluso en el fondo de la\(\left(\mathcal{P} \approx 10^{3}\right.\) barra más profunda\(10-\mathrm{km}\) del pozo oceánico\(\left.\approx 0.1 \mathrm{GPa}\right)\), la densidad del agua aumenta en casi casi\(5 \%\). Como resultado, en la mayoría de los experimentos a escala humana, el agua puede tratarse como incompresible, condición que será ampliamente utilizada en el próximo capítulo. Muchos sólidos son aún mucho menos compresibles ver, por ejemplo, las dos primeras filas del Cuadro 1.

Naturalmente, los medios más compresibles son los gases. Para una porción de gas,\(\mathcal{P}\) es necesaria una cierta presión de fondo solo para contenerla dentro de su volumen\(V\), de manera que la Ec. (36) sólo es válida para pequeños incrementos de presión,\(\Delta \mathcal{P}\):\[\frac{\Delta V}{V}=-\frac{\Delta \mathcal{P}}{K} .\] Además, la compresión de gases también depende de las condiciones termodinámicas. (En contraste, para la mayoría de los medios condensados, los efectos de temperatura son muy pequeños). Por ejemplo, en condiciones ambientales la mayoría de los gases están razonablemente bien descritos por la ecuación de estado para el modelo llamado el gas clásico ideal:\[\mathcal{P} V=N k_{\mathrm{B}} T, \quad \text { i.e. } \mathcal{P}=\frac{N k_{\mathrm{B}} T}{V} .\] donde\(N\) está el número de moléculas en volumen\(V\), y\(k_{\mathrm{B}} \approx 1.38 \times 10^{-23} \mathrm{~J} / \mathrm{K}\) es la constante de Boltzmann. \({ }^{11}\)Para un pequeño cambio de volumen\(\Delta V\) a una temperatura constante\(T\), esta ecuación da\[\left.\Delta \mathcal{P}\right|_{T=\mathrm{const}}=-\frac{N k_{\mathrm{B}} T}{V^{2}} \Delta V=-\frac{\mathcal{P}}{V} \Delta V, \quad \text { i.e. }\left.\frac{\Delta V}{V}\right|_{T=\mathrm{const}}=-\frac{\Delta \mathcal{P}}{P} .\] Comparando esta expresión con la Ec. (36), obtenemos un resultado notablemente simple para la compresión isotérmica de gases,\[\left.K\right|_{T=\mathrm{const}}=\mathcal{P},\] lo que significa en particular que el módulo volumétrico enumerado en El Cuadro 1 es realmente válido, en las condiciones ambientales, para casi cualquier gas. Obsérvese, sin embargo, que el cambio de las condiciones termodinámicas (digamos, de isotérmicas a adiabáticas\({ }^{12}\)) puede afectar la compresibilidad del gas. Ahora consideremos el segundo experimento fundamental, bastante diferente: una deformación puramente cortante que se muestra en la Figura 2. Dado que las trazas de las matrices (15) y (20), que describen esta situación, son iguales a 0, por sus elementos fuera de diagonal, la ecuación (32) da meramente\(\sigma_{j j}\) '\(=2 \mu s_{j j}\), de manera que el ángulo de deformación\(\alpha\) (ver Figura 2) es justo\[\alpha=\frac{1}{\mu} \frac{F}{A} .\] Tenga en cuenta que el ángulo no depende del espesor \(h\)de la muestra, aunque por supuesto la deformación lineal máxima\(q_{x}=\alpha h\) es proporcional al espesor. Naturalmente, como muestra el Cuadro 1,\(\mu=0\) para todos los fluidos, ya que no resisten el esfuerzo de cizallamiento estático.

Sin embargo, no todas las situaciones, incluso las aparentemente simples, involucran solo una o una\(K\) o\(\mu\). Consideremos estirar una varilla elástica larga y delgada de una sección transversal uniforme del área\(A\), el llamado experimento de esfuerzo de tracción que se muestra en la Figura\(6.13\)

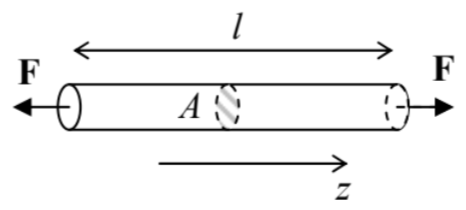Figura 7.6. El experimento de tensión de tracción.

Aunque la deformación de la varilla cerca de sus extremos sujetos depende de la forma exacta en que se\(\mathbf{F}\) aplican las fuerzas (discutiremos este tema más adelante), podemos esperar que en la mayor parte de su longitud las fuerzas de tensión se dirijan virtualmente a lo largo de la varilla,\(d \mathbf{F}=F_{z} \mathbf{n}_{z}\) y por lo tanto, con la elección de coordenadas que se muestra en Figura\(6, \sigma_{x j}=\sigma_{y j}=0\) para todos\(j\), incluyendo los elementos diagonales\(\sigma_{x x}\) y\(\sigma_{y y}\). Además, debido a las superficies laterales abiertas, sobre las cuales, evidentemente\(d F_{x}=d F_{y}=0\), no puede existir una fuerza de tensión interna de ninguna dirección, actuando sobre ningún límite interno elemental paralelo a estas superficies. Esto significa que\(\sigma_{z x}=\)\(\sigma_{z y}=0\). Entonces, de todos los componentes del tensor de tensión solo uno\(\sigma_{z z}\),, no es igual a cero, y para una muestra uniforme,\(\sigma_{z z}=\) const\(=F / A\). Para este caso, la Ec. (34) muestra que el tensor de deformación también es diagonal, pero con diferentes elementos diagonales:\[\begin{gathered} s_{z z}=\left(\frac{1}{9 K}+\frac{1}{3 \mu}\right) \sigma_{z z}, \\ s_{x x}=s_{y y}=\left(\frac{1}{9 K}-\frac{1}{6 \mu}\right) \sigma_{z z} . \end{gathered}\] Dado que el esfuerzo de tracción es más común en la práctica de ingeniería (y en el diseño de experimentos físicos), ambas combinaciones de los módulos elásticos que participan en estas dos relaciones han merecido sus propios nombres. En particular, la constante en la ecuación (42) suele denotarse como\(1 / E\) (pero en muchos textos, as\(1 / Y\)), donde\(E\) se llama módulo de Young: 14

\[\frac{1}{E} \equiv \frac{1}{9 K}+\frac{1}{3 \mu}, \quad \text { i.e. } E \equiv \frac{9 K \mu}{3 K+\mu}\]Como muestra la Figura 6, en la geometría de tensión de\(s_{z z} \equiv \partial q_{z} / \partial z=\Delta l / l\) manera que el módulo de Young escala la relación lineal entre la extensión relativa de la varilla y la fuerza aplicada por unidad de área:\({ }^{15}\)\[\frac{\Delta l}{l}=\frac{1}{E} \frac{F}{A} \text {. }\] La tercera columna de la Tabla 1 anterior muestra los valores de este módulo para dos bien conocidos sólidos: diamante (con el mayor valor conocido\(E\) de todos los materiales a granel\({ }^{16}\)) y los aceros (soluciones sólidas\(\sim 10 \%\) de carbono en hierro) utilizados en la construcción. Nuevamente, para todos los fluidos, el módulo de Young es igual a cero, como se desprende de la Ec. (44) para\(\mu=0\).

Confío en que el lector de estas notas ha estado familiarizado con la Ec. (42), en la forma de la Ec. (45), desde sus estudios de pregrado. Sin embargo, lo más probable es que esto no se pueda decir de su contraparte, la ecuación (43), lo que demuestra que a la tensión de tracción, las dimensiones de la sección transversal de la varilla también cambian. Este efecto generalmente se caracteriza por la siguiente relación adimensional de Poisson:\({ }^{17}\)\[-\frac{s_{x x}}{s_{z z}}=-\frac{s_{y y}}{s_{z z}}=-\left(\frac{1}{9 K}-\frac{1}{6 \mu}\right) /\left(\frac{1}{9 K}+\frac{1}{3 \mu}\right)=\frac{1}{2} \frac{3 K-2 \mu}{3 K+\mu} \equiv v,\] De acuerdo con esta fórmula, para materiales realistas con\(K>0, \mu \geq 0, v\) pueden variar de (-1) a\((+1 / 2)\), pero para la gran mayoría de los materiales,\({ }^{18}\) sus valores están entre 0 y\(1 / 2-\) ver el columna correspondiente del Cuadro 1. El límite inferior de este rango se alcanza en materiales porosos como el corcho, cuyas dimensiones laterales casi no cambian a la tensión de tracción. Algunos materiales blandos como los cauchos naturales y sintéticos presentan el caso contrario:\(v \approx 1 / 2 .{ }^{19}\) Ya que según las Eqs. \((13)\)y\((42)\), el cambio de volumen es\[\frac{\Delta V}{V}=s_{x x}+s_{y y}+s_{z z}=\frac{1}{E} \frac{F}{A}(1-2 v) \equiv(1-2 v) \frac{\Delta l}{l},\] tales materiales prácticamente no cambian su volumen a la tensión de tracción. El límite último de esta tendencia,\(\Delta V / V=0\), es proporcionado por fluidos y gases, pues, como se desprende de la Ec. (46) con\(\mu=0\), su relación de Poisson\(v\) es exactamente\(1 / 2\). Sin embargo, para la mayoría de los materiales de construcción practicables como varios aceros (ver Cuadro 1) el cambio de volumen (47) es tan alto como\(\sim 40 \%\) el de la longitud.

Debido al claro sentido físico de los coeficientes\(E\) y\(v\), frecuentemente se utilizan como un par de módulos elásticos independientes, en lugar de\(K\) y\(\mu\). Resolviendo las ecuaciones (44) y (46) para ellas, obtenemos\[K=\frac{E}{3(1-2 v)}, \quad \mu=\frac{E}{2(1+v)} .\] Usando estas fórmulas, las dos formulaciones (equivalentes) de la ley de Hooke, expresadas por las ecuaciones (32) y (34), pueden reescribirse como\[\begin{aligned} \sigma_{i j^{\prime}} &=\frac{E}{1+v}\left(s_{i j^{\prime}}+\frac{v}{1-2 v} \operatorname{Tr}(\mathrm{s}) \delta_{j j^{\prime}}\right) \\ s_{i j^{\prime}} &=\frac{1+v}{E}\left(\sigma_{i j^{\prime}}-\frac{v}{1+v} \operatorname{Tr}(\sigma) \delta_{i j^{\prime}}\right) \end{aligned}\] La relación lineal entre el tensor de tensión y tensión en continua elástica permite un paso más en nuestro cálculo de la energía potencial\(U\) debido a la deformación, iniciada al final de\(\mathrm{Sec} .2 .\) Efectivamente, a cada parte infinitesimal de este aumento de tensión, podemos aplicar la Eq. (30), con el trabajo elemental\(\delta \mathscr{W}\) de las fuerzas superficiales aumentando la energía potencial de “nuestra” parte del cuerpo por igual cantidad \(\delta U\). Aumentemos lentamente la deformación desde un estado completamente desforzado (en el que podemos tomar\(U=0\)) a un cierto estado tensado, en ausencia de fuerzas a granel\(\mathbf{f}\), manteniendo intacto el tipo de deformación, es decir, la relación entre los elementos del tensor de tensión. En este caso, todos los elementos del tensor\(\sigma_{i j}\) 'son proporcionales al mismo parámetro único que caracteriza la tensión (digamos, la fuerza total aplicada), y según la ley de Hooke, todos los elementos del tensor también\(s_{j j}\) son proporcionales a ese parámetro. En este caso, la integración de la Ec. (30) a través de la variación produce el siguiente valor final: 20\[U=\int_{V} u(\mathbf{r}) d^{3} r, \quad u(\mathbf{r})=\frac{1}{2} \sum_{j, j^{\prime}=1}^{3} \sigma_{i j^{\prime}} S_{j j} .\] Evidentemente, esto\(u(\mathbf{r})\) puede interpretarse como la densidad volumétrica de la energía potencial de la deformación elástica.

---

\({ }^{8}\)El nombre de Robert Hooke (1635-1703), el polímata que fue el primero en describir la ley en su versión más simple, 1D.

\({ }^{9}\)Dado que los elementos tensores de deformación, definidos por la Ec. (9), son adimensionales, mientras que la deformación, definida por la Ec. (18), tiene la dimensionalidad similar a la presión (de fuerza por unidad de área), también lo hacen los módulos elásticos\(K\) y\(\mu\).

\({ }^{10}\)Se puede probar que tal situación puede implementarse no solo en un fluido con presión\(\mathcal{P}\) sino también en una muestra sólida de forma arbitraria, por ejemplo colocándola en un fluido comprimido.

\({ }^{11}\)Para la derivación y una discusión detallada de la Ec. (37) véase, e.g., SM Sec. 3.1.

\({ }^{12}\)Véase, por ejemplo, SM Sec. 1.3.

\({ }^{13}\)Aunque el análisis de compresión en esta situación da resultados similares, en experimentos prácticos una fuerte compresión de una muestra larga puede llevar a la pérdida de la estabilidad horizontal -el llamado pandeo- de la varilla.

\({ }^{14}\)El nombre de otro polímata, Thomas Young (1773-1829) -algo injustamente, porque su trabajo sobre la elasticidad fue anterior a un análisis teórico de L. Euler en 1727 y experimentos detallados de Giordano Riccati en 1782.

\({ }^{15}\)De acuerdo con la Ec. (47),\(E\) puede pensarse como la fuerza por unidad de área, que duplicaría la longitud de la muestra inicial, si tan solo la ley del Hooke fuera válida para deformaciones tan grandes, ya que normalmente no lo es.

\({ }^{16}\)Probablemente sea algo mayor (hasta 2,000 GPa) en nanoestructuras tales como nanotubos de carbono y láminas monatómicas (grafeno), aunque aún existe una incertidumbre sustancial en los módulos elásticos medidos experimentalmente de estas estructuras -para una revisión ver, e.g., G. Dimitrios et al., Prog. Mater. Sci. 90, 75 (2017).

\({ }^{17}\)En algunos textos más antiguos, se denota la relación de Poisson\(\sigma\), pero su notación como\(v\) domina la literatura moderna.

\({ }^{18}\)Las únicas excepciones conocidas son ciertos sólidos exóticos con microestructura interna muy específica - véase, p. ej.,\(R\). Lakes, Science 235, 1038 (1987) y referencias en los mismos.

\({ }^{19}\)Por ejemplo, los cauchos de silicona (polímeros sintéticos ampliamente utilizados en el diseño de experimentos de ingeniería y física) tienen, dependiendo de su composición particular, síntesis y curado térmico\(v=0.47 \div 0.49\), y como resultado combinan módulos a granel respetables\(K=(1.5 \div 2)\) GPa con módulos de Young muy bajos: \(E=(0.0001 \div 0.05)\)GPa.

\({ }^{20}\)Para mayor claridad, permítanme reproducir esta integración para la extensión de un simple resorte 1D. En este caso,\(\delta U=\delta \mathscr{W}=\)\(F \delta x\), y si la fuerza del resorte es elástica\(F=\kappa x\), la integración cede\(U=\kappa x^{2} / 2 \equiv F x / 2\).