9.3: Caos en los sistemas hamiltonianos

La última conclusión, por supuesto, es válida para los sistemas hamiltonianos, que son solo un tipo particular de sistemas dinámicos. Sin embargo, uno puede preguntarse si estos sistemas, que cuentan con al menos una primera integral de movimiento,\(H=\) const, y por lo tanto están más “ordenados” que los sistemas discutidos anteriormente, pueden exhibir caos en absoluto. La respuesta es sí porque tales sistemas aún pueden tener mecanismos de crecimiento exponencial de una pequeña perturbación inicial.

Como la forma más sencilla de demostrarlo, consideremos el llamado billar matemático, es decir, sistema con una partícula balística (una “bola”) que se mueve libremente por inercia sobre una superficie plana horizontal (“mesa”) limitada por paredes rígidas impenetrables. En este modelo idealizado del juego habitual de billar, la velocidad de la pelota\(\mathbf{v}\) se conserva cuando se mueve sobre la mesa, y cuando choca contra una pared, la pelota se refleja elásticamente desde ella como desde un espejo,\({ }^{14}\) con la inversión del signo de la velocidad normal\(v_{n}\), y la conservación de la velocidad tangencial\(v_{\tau}\), y por lo tanto sin pérdida alguna de su energía cinética (y de ahí la plena)\[E=H=T=\frac{m}{2} v^{2}=\frac{m}{2}\left(v_{n}^{2}+v_{\tau}^{2}\right) .\] Este modelo, si bien es un sistema\(2 \mathrm{D}\) dinámico legítimo,\({ }^{15}\) permite realizar análisis geométricos para varias formas de tabla simples. El caso más sencillo es un billar rectangular de área\(a \times b\) (Figura 7), cuyo análisis puede llevarse a cabo fácilmente con solo la sustitución de cada evento de reflexión de bola por el reflejo espejo de la mesa en esa pared - ver las líneas discontinuas en el panel (a).

Figura 9.7. Movimiento de la bola en un billar rectangular en (a) un acorde, y (b) un ángulo de lanzamiento inconmensurable.

Tal análisis (dejado para el placer del lector: -) muestra que si la tangente del ángulo de lanzamiento de la bola\(\varphi\) es proporcional a la relación de longitud lateral:\[\tan \varphi=\pm \frac{m}{n} \frac{b}{a},\] donde\(n\) y\(m\) son enteros no negativos sin multiplicadores enteros comunes, la bola regresa exactamente al punto de lanzamiento \(\mathrm{O}\), después de los\(m\) tiempos de rebote de cada pared de longitud\(a\) y los\(n\) tiempos de cada pared de longitud\(b\). (Las líneas rojas en la Figura 7a muestran un ejemplo de tal trayectoria para\(n=m=1\), mientras que las líneas azules, para\(m=3, n=1 .\)) Cuanto mayor es la suma\((m+n)\), más compleja es tal trayectoria cerrada - “órbita”. Finalmente, si\((n+m) \rightarrow \infty\), es decir,\(\tan \varphi\) y\(b / a\) son inconmensurables (es decir, que su relación es un número irracional), la trayectoria cubre toda el área de la mesa, y la pelota nunca regresa exactamente al punto de lanzamiento. Aún así, esto no es un auténtico caos. En efecto, un pequeño desplazamiento del punto de lanzamiento\(\mathrm{O}\) desplaza todos los fragmentos de trayectoria por el mismo desplazamiento. Además, en cualquier momento\(t\), cada uno de los componentes cartesianos\(v_{j}(t)\) de la velocidad de la pelota (con ejes de coordenadas paralelos a los lados de la mesa) puede tomar solo dos valores\(\pm v_{j}(0)\), y por lo tanto puede variar solo tanto como se está cambiando la velocidad inicial.

En 1963, es decir, mucho antes de la obra de E. Lorenz, Yakov Sinaí demostró que la situación cambia completamente si se inserta una pared adicional, en forma de círculo, en el billar rectangular (Figura 8). Para la mayoría de las condiciones iniciales, la trayectoria de la pelota finalmente corre hacia el círculo (ver la línea roja en el panel (a) como ejemplo), y la trayectoria adicional se vuelve esencialmente caótica. En efecto, consideremos el reflejo de la pelota desde la pared en forma de círculo - Figura 8b. Debido a la conservación de la velocidad tangencial, y al cambio de signo de la componente de velocidad normal, la reflexión obedece a una simple ley:\(\theta_{\mathrm{r}}=\theta_{1}\). La figura\(8 \mathrm{~b}\) muestra que como resultado, la magnitud de una pequeña diferencia\(\delta \varphi\) entre los ángulos de dos trayectorias cercanas (medidas en el sistema de laboratorio), se duplica en cada reflexión desde la pared curva. Esto significa que la pequeña desviación crece a lo largo de la trayectoria de la bola como\[|\delta \varphi(N)| \sim|\delta \varphi(0)| \times 2^{N} \equiv|\delta \varphi(0)| e^{N \ln 2},\] donde\(N\) está el número de reflexiones de la pared convexa. \({ }^{16}\)Como ya sabemos, tal divergencia exponencial de trayectorias, con un exponente positivo de Lyapunov, es la característica principal del caos determinista. \({ }^{17}\)

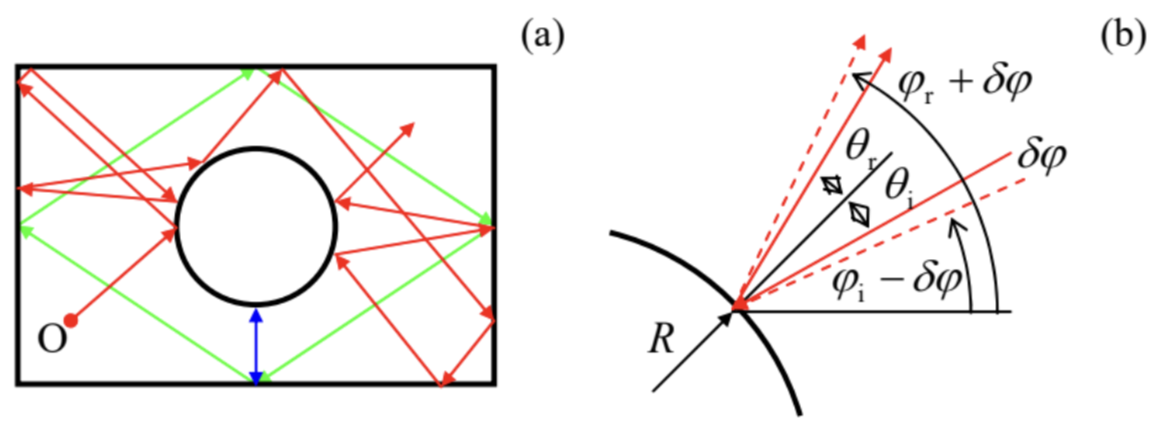Figura 9.8. a) Movimiento sobre una mesa de billar sinaí, y b) el mecanismo de divergencia exponencial de trayectorias cercanas.

La novedad más importante del caos dinámico en los sistemas hamiltonianos es su dependencia de las condiciones iniciales. (En los sistemas discutidos en los dos apartados anteriores, que carecen de las integrales del movimiento, las condiciones iniciales se “olvidan” rápidamente, y el caos suele caracterizarse después de un periodo transitorio inicial - véase, por ejemplo, la Figura 4.) En efecto, incluso un billar Sinaí permite el movimiento periódico, a lo largo de órbitas cerradas, en ciertas condiciones iniciales - ver las líneas azul y verde en la Figura 8a como ejemplos. Así, la “profundidad” del caos en tales sistemas puede caracterizarse por el “fraccion"18 del espacio de fase de los parámetros iniciales (para un billar 2D, del espacio 3D de valores iniciales de\(x, y\), y\(\varphi\)) dando como resultado trayectorias caóticas.

Esta conclusión también es válida para los sistemas hamiltonianos que se cumplen en el experimento con mayor frecuencia que los billares, por ejemplo, osciladores no lineales acoplados sin amortiguamiento. Quizás el ejemplo más antiguo y más popular es el llamado sistema Hénon-Heiles,\({ }^{19}\) que puede ser descrito por la siguiente función lagrangiana:\[L=\frac{m_{1}}{2}\left(\dot{q}_{1}^{2}-\omega_{1}^{2} q_{1}^{2}\right)+\frac{m_{2}}{2}\left(\dot{q}_{2}^{2}-\omega_{2}^{2} q_{2}^{2}\right)-\varepsilon\left(q_{1}^{2}-\frac{1}{3} q_{2}^{2}\right) q_{2} .\]\[\begin{aligned} &m_{1}\left(\ddot{q}_{1}+\omega_{1}^{2} q_{1}\right)=-2 \varepsilon q_{1} q_{2}, \\ &m_{2}\left(\ddot{q}_{2}+\omega_{2}^{2} q_{2}\right)=-\varepsilon\left(q_{1}^{2}-q_{2}^{2}\right), \end{aligned}\] y encontrar su primera integral de movimiento (físicamente, la ley de conservación de energía):\[H=E=\frac{m_{1}}{2}\left(\dot{q}_{1}^{2}+\omega_{1}^{2} q_{1}^{2}\right)+\frac{m_{2}}{2}\left(\dot{q}_{2}^{2}+\omega_{2}^{2} q_{2}^{2}\right)+\varepsilon\left(q_{1}^{2}-\frac{1}{3} q_{2}^{2}\right) q_{2}=\text { const . }\] En el contexto de nuestras discusiones en los Capítulos 5 y 6, las ecuaciones (19) pueden interpretarse fácilmente como aquellas que describen dos osciladores, con frecuencias de pequeña oscilación\(\omega_{1}\) y\(\omega_{2}\), acopladas solo como se describe por los términos cuadráticos en los lados derecho de las ecuaciones. Esto significa que como las amplitudes de oscilación\(A_{1,2}\), y por lo tanto la energía total\(E\) del sistema, son cercanas a cero, los subsistemas osciladores son prácticamente independientes, cada uno realizando oscilaciones sinusoidales a su propia frecuencia. Esta observación sugiere una manera conveniente de representar el movimiento del sistema. \({ }^{20}\)Consideremos un plano Poincaré para uno de los osciladores (digamos, con la coordenada\(q_{2}\)), similar al discutido en la Sec. 2 anterior, con la única diferencia es que (por la ausencia de una función explícita del tiempo en las ecuaciones del sistema), la trayectoria en el plano de fase \(\left[q_{2}, \dot{q}_{2}\right]\)se destaca en los momentos en que\(q_{1}=0\).

Partimos desde el límite\(A_{1,2} \rightarrow 0\), cuando las oscilaciones de\(q_{2}\) son prácticamente sinusoidales. Como ya sabemos (ver Figura\(5.9\) y su discusión), si el resaltado del punto de representación fuera perfectamente sincrónico con la frecuencia\(\omega_{2}\) de las oscilaciones, solo habría un punto en el plano de Poincaré - ver, por ejemplo, el panel superior derecho de la Figura 4. Sin embargo, en el\(q_{1}\) resaltado iniciado, no existe tal sincronismo, de manera que cada periodo, se resalta un punto diferente de la trayectoria elíptica (a la escala apropiada de la velocidad, circular), de manera que los puntos resultantes, para ciertas condiciones iniciales, residen en un círculo de radio \(A_{2}\). Si ahora variamos las condiciones iniciales, es decir, redistribuimos la energía inicial entre los osciladores, pero mantenemos\(E\) constante la energía total, en el plano de Poincaré obtenemos un conjunto de elipses.

Ahora bien, si se incrementa la energía inicial, la interacción no lineal de las oscilaciones comienza a deformar estas elipses, provocando también sus cruces -véase, por ejemplo, el panel superior izquierdo de la Figura 9. Aún así, por debajo de cierto valor umbral de\(E\), todos los puntos de Poincaré pertenecientes a una determinada condición inicial se sientan en un solo contorno cerrado. Además, estos contornos pueden calcularse aproximadamente, pero con bastante buena precisión, utilizando la generalización directa del método discutido en la Sec. 5.2.21

Figura 9.9. Planos Poincaré del sistema HénonHeiles (19), en notación\(y \equiv \varepsilon q_{2}\), para tres valores de la energía adimensional\(e \equiv E / E_{0}\), con\(E_{0} \equiv m_{1} \omega_{1}{ }^{2} / \varepsilon^{2}\). Adaptado de M. Hénon y C. Heiles, The Astron. J.\(\mathbf{6 9}, 73\) (1964). \ odot AAS, reproducido con permiso.

Sin embargo, a partir de algún valor de energía, ciertas condiciones iniciales conducen a secuencias de puntos dispersos sobre partes del plano de Poincaré, con un área distinta de cero - ver el panel superior derecho de la Figura\(9 .\) Esto significa que las oscilaciones correspondientes\(q_{2}(t)\) no se repiten de un (cuasi-) periodo a el siguiente\(-\) cf. Figura 4 para el péndulo disipativo forzado. Esto es caos. \({ }^{22}\)Sin embargo, algunas otras condiciones iniciales aún conducen a contornos cerrados. Esta característica es similar a la del billar Sinaí, y es típica de los sistemas hamiltonianos. A medida que aumenta la energía, partes cada vez más grandes del plano de Poincaré corresponden al movimiento caótico, lo que significa un caos cada vez más profundo - ver el panel inferior de la Figura 9.

---

\({ }^{14}\)Un nombre que suena más científico para tal reflexión es especular, del vocablo latino “espéculo” que significa espejo metálico.

\({ }^{15}\)En efecto, se describe completamente por la siguiente función lagrangiana:\(L=m v^{2} / 2-U(\rho)\), con\(U(\rho)=0\) para los vectores de\(2 \mathrm{D}\) radio\(\rho\) pertenecientes al área de la mesa, y\(U(\rho)=+\infty\) fuera del área.

\({ }^{16}\)Superficialmente, la Ec. (17) también es válida para una pared plana, pero como se discutió anteriormente, un billar con tales paredes presenta una correlación completa entre reflexiones secuenciales, de manera que el ángulo\(\varphi\) siempre vuelve a su valor inicial. En un billar sinaí, tal correlación desaparece. Las paredes cóncavas también pueden hacer caótico a un billar; un ejemplo famoso es el billar del estadio, sugerido por Leonid Bunimovich en 1974, con dos paredes rectas paralelas que conectan dos paredes semicirculares cóncavas. Otro ejemplo, que permite un análisis directo (realizado por primera vez por Martin Gutzwiller en la década de 1980), es el llamado billar Hadamard: una mesa infinita (o rectangular) con una superficie no horizontal de curvatura negativa.

\({ }^{17}\)Los billares de pared curva también son una plataforma conveniente para estudios de propiedades cuánticas de sistemas clásicamente caóticos (para su discusión conceptual, ver QM Sec. 3.5), en particular, las características llamadas “cicatrices cuánticas” ver, por ejemplo, los espectaculares resultados de simulación numérica de E. Heller, Phys. Rev. Lett. \(\mathbf{5 3}, 1515\)(1984).

\({ }^{18}\)En realidad, la caracterización cuantitativa de la fracción no es trivial, ya que puede tener dimensionalidad fractal. Desafortunadamente, por falta de tiempo tengo que referir al lector interesado en este número a literatura especial, por ejemplo, la monografía de B. Mandelbrot (citada anteriormente) y referencias en ella.

\({ }^{19}\)Fue estudiado por primera vez en 1964 por Michel Hénon y Carl Heiles como un simple modelo de rotación estelar alrededor de un centro galáctico. La mayoría de los estudios de esta ecuación se han realizado para el siguiente caso particular:\(m_{2}=2 m_{1}, m_{1} \omega_{1}{ }^{2}=\)\(m_{2} \omega_{2}{ }^{2}\). En este caso, introduciendo nuevas variables\(x \equiv \varepsilon q_{1}, y \equiv \varepsilon q_{2}\), y\(\tau \equiv \omega_{1} t\), es posible reescribir las ecuaciones (18) - (20) en formas libres de parámetros. Todos los resultados que se muestran en la Figura 9 a continuación son para este caso.

\({ }^{20}\)Generalmente, el sistema tiene una trayectoria en el espacio 4D, por ejemplo, la de las coordenadas\(q_{1,2}\) y sus derivadas de tiempo, aunque la primera integral del movimiento (20) significa que por cada energía fija\(E\), el movimiento se limita a un subespacio 3D. Aún así, esta es una dimensión demasiado para una representación conveniente del movimiento.

\({ }^{21}\)Véase, por ejemplo, M. Berry, en: S. Jorna (ed.), Topics in Nonlinear Dynamics, AIP Conf. Proc. No. 46, AIP, 1978, pp. 16-120.

\({ }^{22}\)Este hecho cumple con la condición necesaria de caos, discutida al final de la Sec. 2 porque las ecuaciones (19) pueden reescribirse como un sistema de cuatro ecuaciones diferenciales de primer orden.