10.5: Problemas de ejercicio

En cada uno de los Problemas 10.1-10.3, para el sistema dado:

(i) derivar las ecuaciones de movimiento de Hamilton, y

(ii) comprobar si las ecuaciones son equivalentes a las derivadas del formalismo lagrangiano.

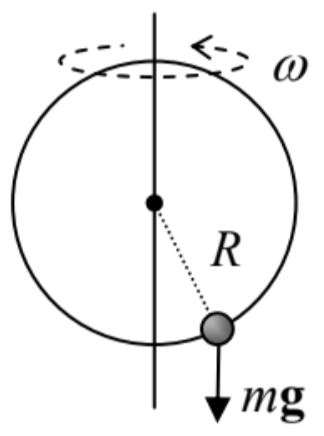
10.1. Nuestro sistema “testbed”: una perla sobre un anillo, siendo girada con una velocidad angular fija\(\omega\) alrededor de su diámetro vertical\(-\) ver Figura 2.1, reproducida a la derecha.

10.2. El sistema considerado en Problema 2.3: un péndulo colgado de un soporte horizontal cuya ley de movimiento\(x_{0}(t)\) es fija - ver la figura de la derecha. (Sin restricción de plano vertical.)

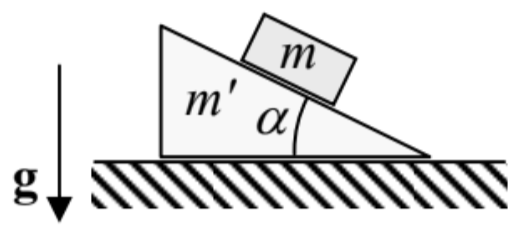
10.3. El sistema considerado en el Problema 2.8: un bloque de masa\(m\) que puede deslizarse, sin fricción, a lo largo de la superficie inclinada de una pesada cuña de masa\(m\) '. La cuña es libre de moverse, también sin fricción, a lo largo de una superficie horizontal - vea la figura a la derecha. (Ambos movimientos están dentro del plano vertical que contiene la línea de pendiente más pronunciada).

10.4. Encuentra y resuelve las ecuaciones de movimiento de una partícula con la siguiente función hamiltoniana:\[H=\frac{1}{2 m}(\mathbf{p}+a \mathbf{r})^{2},\] donde\(a\) es un escalar constante.

10.5. \(L\)Sea la función lagrangiana, y\(H\) la función hamiltoniana, del mismo sistema. ¿Qué tres de las siguientes cuatro declaraciones,

i)\(\frac{d L}{d t}=0\),

ii)\(\frac{\partial L}{\partial t}=0\),

iii)\(\frac{d H}{d t}=0\),

iv)\(\frac{\partial H}{\partial t}=0\),

son equivalentes? Dé un ejemplo cuando esas tres igualdades se mantienen, pero la cuarta no.

10.6. Calcular los corchetes de Poisson de un componente cartesiano\(\mathbf{L}\) del momento angular de una partícula que se mueve en un campo de fuerza central y su función hamiltoniana\(H\), y discutir la implicación más evidente del resultado.

10.7. Después de que se hubieran iniciado pequeñas oscilaciones en el péndulo puntual que se muestra en la Figura de la derecha, la cuerda se está levantando lentamente, de manera que\(l\) se está reduciendo la longitud del péndulo. Descuidando la disipación,

i) demostrar mediante un cálculo directo que la energía de oscilación está cambiando efectivamente proporcionalmente a la frecuencia de oscilación, como se desprende de la constancia de la correspondiente invariante adiabática (40); y

(ii) encontrar la\(l\) -dependencia de las amplitudes de las desviaciones angulares y lineales del equilibrio.

10.8. La masa\(m\) de un cuerpo pequeño que realiza\(1 \mathrm{D}\) oscilaciones en el pozo potencial\(U(x)=a x^{2 n}\), con\(n>0\), se está cambiando lentamente. Calcular la energía de\(E\) oscilación en función de\(m\).

10.9. Una bola rígida está rebotando verticalmente desde el piso de un elevador cuya aceleración ascendente cambia muy lentamente. Descuidando la disipación de energía, calcule cuánto\(h\) cambia la altura de rebote durante el aumento de la aceleración de 0 a\(g\). ¿Tu resultado es válido para un incremento igual pero abrupto de la aceleración del elevador?